Memory Augmented Graph Neural Networks for Sequential Recommendation

目录

• 概
• 符号说明
• MA-GNN
  • Short-term Interest Modeling
• Long-term Interest Modeling
  • Interest Fusion
• 代码

Ma C., Ma L., Zhang Y., Sun J., Liu X. and Coates M. Memory augmented graph neural networks for sequential recommendation. AAAI, 2021.

概

用图提取 short-term interest, 用 memory network 提取 long-term interest.

符号说明

• $\mathcal{S}^u = (I_1, I_2, \ldots, I_{|\mathcal{S}^u|})$, 用户 $u$ 的交互序列;
• $\mathbf{p}_u$, 用户 $u$ 的 embedding;
• $\mathbf{h}_i$, item $i$ 的 embedding;

MA-GNN

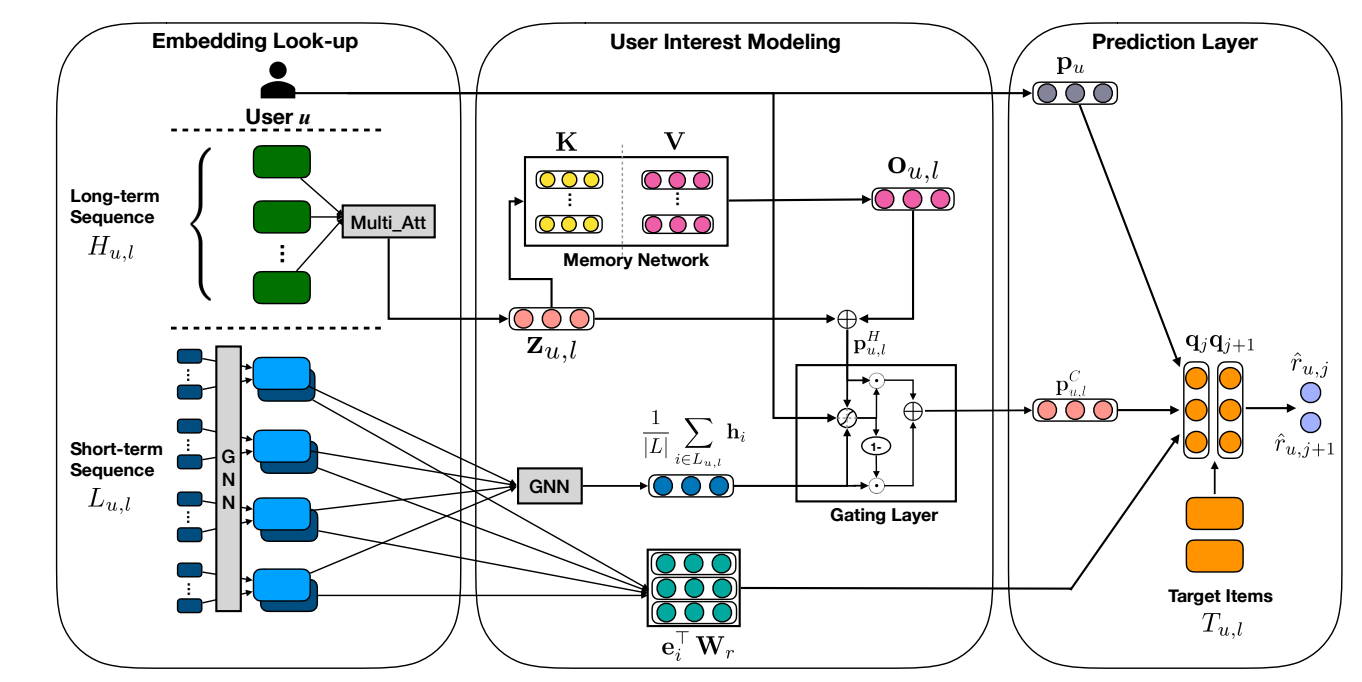
• 总体来说, MA-GNN 分为三条路:
  • Short-term interest;
  • Long-term interest;
  • User embedding.

Short-term Interest Modeling

• 首先, 将序列 $\mathcal{S}^u$ 切分成长度为 $|L$ 的多个子序列:

  $$L_{u, l} = (I_l, I_{l+1}, \ldots, I_{l + |L| - 1}),$$

  训练中, 我们会用该子序列去预测接下来的 $|T|$ items.

• 子序列 $L_{u, l}$ 可以理解为某一阶段的用户的短期兴趣, MA-GNN 利用 Item Graph 来建模这一部分. 对于序列 $L_{u,l}$, 对于结点 $u \not= v \in L_{u, l}$, 两个结点间存在边若 $d(u, v) < 3$, $d(u, v)$ 表示在序列中 $(u, v)$ 之间的最小的间隔. 如上图所示, 设经过行归一化后的邻接矩阵为 $A$.

• 接着, 我们用两层的图网络来提取 short-term interest:

  $$\mathbf{h}_i = \tanh (\mathbf{W}^{(1)} \cdot [\sum_{k \in \mathcal{N}_i} \mathbf{e}_k A_{i, k}; \mathbf{e}_i]), \forall i \in L_{u, l} \\ \mathbf{p}_{u, l}^S = \tanh (\mathbf{W}^{(2)} \cdot [\frac{1}{|L|}] \sum_{i \in L_{u, i}} \mathbf{h}_i; \mathbf{p}_u).$$

  这里 $\mathcal{N}_i$ 是限定 $L_{u, l}$ 中的一阶邻居, $[\cdot; \cdot]$ 是拼接操作.

Long-term Interest Modeling

• 首先定义

  $$H_{u, l} = (I_1, I_2, \ldots, I_{l-1}),$$

  为 $L_{u, l}$ 之前的交互信息.

• 首先通过注意力得到一个向量表示:

  $$\mathbf{H}_{u, l} := \mathbf{H}_{u, l} + \text{PE}(H_{u, l}), \\ \mathbf{S}_{u, l} = \text{softmax}(\mathbf{W}_a^{(3)} \tanh(\mathbf{W}_a^{(1)}\mathbf{H}_{u, l} + (\mathbf{W}_a^{(2)}\mathbf{p}_u) \otimes \bm{1}_{\phi})) \in \mathbb{R}^{h \times |H_{u, i}|} \\ \mathbf{Z}_{u, l} = \tanh(\mathbf{S}_{u, l} \cdot \mathbf{H}_{u,l}^T) \in \mathbb{R}^{h \times d} \\ \mathbf{z}_{u, l} = \text{avg}(\mathbf{Z}_{u, l}) \in \mathbb{R}^d.$$

  其中 $\mathbf{H}_{u,l}$ 为对应 item 的向量表示矩阵, $\text{PE}(\cdot)$ 为 sinusoidal positional encoding, $\otimes$ 表示外积.

• 接下来, 将 query $\mathbf{z}_{u, l}$ 通过 Memory network

  $$\begin{align} s_i = \text{softmax}(\mathbf{z}_{u, l}^T \cdot \mathbf{k}_i), \\ \mathbf{o}_{u, l} = \sum_{i} s_i \mathbf{v}_i, \\ \mathbf{p}_{u, l}^H = \mathbf{z}_{u, l} + \mathbf{o}_{u, l}. \end{align}$$

  其中 $\mathbf{k}_i, \mathbf{v}_i$ 分别来自 $\mathbf{K}, \mathbf{V} \in \mathbb{R}^{d \times m}$ 的第 $i$ 列. 我们可以认为, $\mathbf{K}, \mathbf{V}$ 中学习到了一些不同的偏好的原型, 通过加权求和, 我们找到了对于 $u$ 的 $l$ 之前的偏爱的建模.

Interest Fusion

• 最后, 通过 LSTM 来将二者融合:

  $$\mathbf{g}_{u, l} = \sigma(\mathbf{W}_g^{(1)} \cdot \frac{1}{|L|} \sum_{i \in L_{u, l}} \mathbf{h}_i + \mathbf{W}_g^{(2)} \cdot \mathbf{p}_{u, l}^{H} + \mathbf{W}_g^{(3)} \cdot \mathbf{p}_u), \\ \mathbf{p}_{u, l}^C = \mathbf{g}_{u, l} \odot \frac{1}{|L|} \sum_{i \in L_{u, l}} \mathbf{h}_i + (\bm{1}_d - \mathbf{g}_{u, l}) \odot \mathbf{p}_{u, l}^H.$$

• 并通过 ($\mathbf{q}$ 是可训练的参数):

  $$\hat{r}_{u, j} = \mathbf{p}_u^T \cdot \mathbf{q}_j + (\mathbf{p}_{u, l}^C)^T \mathbf{q}_j + \frac{1}{|L|} \sum_{i \in L_{u, l}} \mathbf{e}_i^T \mathbf{W}_r \mathbf{q}_j.$$

• 利用 BPR 损失进行训练.

代码

[official]