Contrastive Learning for Representation Degeneration Problem in Sequential Recommendation
概
对比学习之于序列推荐.
符号说明
- \(\mathcal{V}\), items;
- \(s = [v_1, v_2, \ldots, v_t]\), \(v_i \in \mathcal{V}, 0 \le i \le t\), 某个序列.
Motivation
-
序列推荐一般使用交叉熵 (二元的或者一般的) 来训练, 即
\[J(s) = -\log p_{\theta}(s) =-\sum_{n=1}^t \log p_{\theta}(v_n |c_n) =-\sum_{n=1}^t \log \frac{\exp(\langle \bm{h}_c, \bm{v}_n \rangle)}{\sum_{v'}^{\mathcal{V}} \exp(\langle \bm{h}_c, \bm{v}' \rangle)}. \]其中 \(c_n = s_{<n}\), 而 \(\bm{h}_c, \bm{v}_n\) 为对应的 embddings.
-
则
\[\frac{\partial J(s)}{\partial \bm{v}^*} = \sum_{n=1}^t \frac{\exp(\langle \bm{h}_c, \bm{v}^* \rangle)}{\sum_{v'}^{\mathcal{V}} \exp(\langle \bm{h}_c, \bm{v}')} \bm{h}_c = \sum_{n=1}^t p(v^*|c_n) \bm{h}_c, \quad \forall v^* \not \in s. \] -
由此可见, 对于那些 rare items, 它的提取几乎就是由那些 popular items 所决定了. 这可能导致, 那些不活跃的 item 的 embeddings 都一致地往差不多的方向进化, 从而趋同:
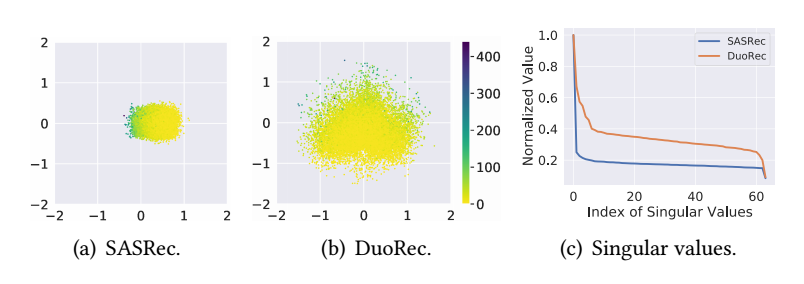
-
从而如上图所示, 大部分 rate items 聚在一处, 而且整体的 embeddings 呈现低秩的情形.
DuoRec
-
根据 embedding matrix \(\bm{V} \in \mathbb{R}^{|\mathcal{V}| \times d}\), positional encoding matrix \(\bm{P} \in \mathbb{R}^{N \times d}\), 从而可以得到:
\[\bm{h}_t^0 = \bm{v}_t + \bm{p}_t, \]每个 item 的 embedding.
-
由此, 对于序列 \(s\) 我们可以得到序列 embeddings: \(\bm{H}^0 = [\bm{h}_0^0, \bm{h}_1^0, \ldots, \bm{h}_t^0]\), 然后通过 Transformer encoder 得到:
\[\bm{H}^L = [\bm{h}_0^L, \bm{h}_1^L, \ldots, \bm{h}_t^L] = \text{Trm}(\bm{H}^0). \]并将 \(\bm{h}_t^L\) 作为该序列的表示.
Contrastive Regularization
-
我们知道, 对比学习有这让相似的样本靠近同时整体特征区域均匀分布的能力, 作者希望借这种能力解决最开始所提出的问题.
-
Dropout 增强: 由于一般的 transformer 架构都包含 dropout, 所以当我们重复进行一次 forward 过程后会得到另一个不同的结果:
\[\bm{H}^{L'} = \text{Trm}(\bm{H}^0), \quad \bm{h}' = \bm{h}_t^{L'} = \bm{H}^{L'}[-1]. \] -
Similar Sequences: 此外, 作者假设若两个 sequences:
\[s_i = [v_{i,1}, v_{i,2}, \ldots, v_{i,t^i}], \\ s_j = [v_{j,1}, v_{j,2}, \ldots, v_{j,t^j}] \\ \]的下一个预测目标 \(v_{i,t^i + 1} = v_{j,t^j+1}\), 则我们认为这两个 sequences 背后的 users 是类似的.
对于序列 \(s\), 我们采样这样的一个近似序列 \(s'\), 然后得到:\[\bm{H}_{s}^{L'} = \text{Trm}({\bm{H}_s^0}'), \quad \bm{h}_s' = \bm{h}_{t,s}^{L'} = \bm{H}_s^{L'}[-1]. \] -
有了这两个不同的视角后, 我们定义:
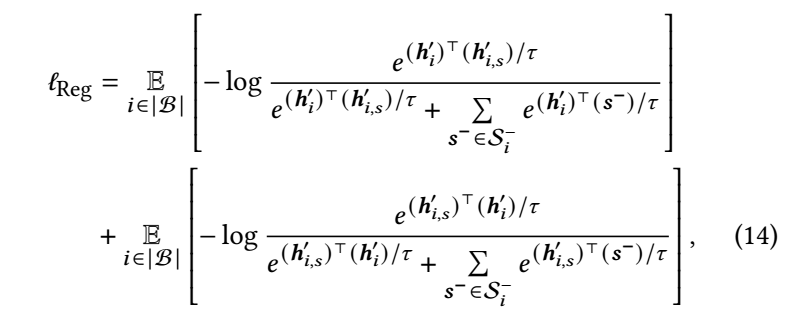
其中 \(\mathcal{S}_1^- = \{\bm{h}_2', \bm{h}_{2, s}', \bm{h}_3', \bm{h}_{3,s}', \ldots, \bm{h}_{|\mathcal{B}|}', \bm{h}_{|\mathcal{B}|, s}'\}\). -
最后的损失为:
\[\ell = \ell_{\text{Rec}} + \lambda \ell_{\text{Reg}}, \\ \ell_{\text{Rec}} = -\text{one-hot}(\bm{y}_i) \log \hat{\bm{y}}_i, \\ \hat{\bm{y}} = \text{softmax}(\bm{Vh}). \]


