Global Context Enhanced Graph Neural Networks for Session-based Recommendation
概
以往的 session 推荐往往只用到 session-level 的图信息, 本文额外用到了全局的图的信息.
符号说明
- \(V = \{v_1, v_2, \ldots, v_m\}\), items;
- \(S = \{v_1^s, v_2^s, \ldots, v_l^s\}\), session;
Session Graph and Global Graph

Session Graph
-
一般的 session graph 如上图 (a) 所示, 就是若 \((u, v)\) 之间存在关系 \(u \rightarrow\) 则俩个结点间存在一条边.
-
作者额外引入了 4 种边的关系: \(r_{in}, r_{out}, r_{in-out}, r_{self}\).
Global Graph
- 首先作者定义了一个结点 \(v\) 的 \(\epsilon\)-Neighbor set:\[\mathcal{N}_{\epsilon}(v) = \{v_j: v_j \in S, v_i \in S, j \in [i - \epsilon, i + \epsilon], v_i = v\}, \]用人话解释就是所有包含 \(v\) 的序列的 \(v\) 前后 \(\epsilon\) 内的结点的集合.
GCE-GNN
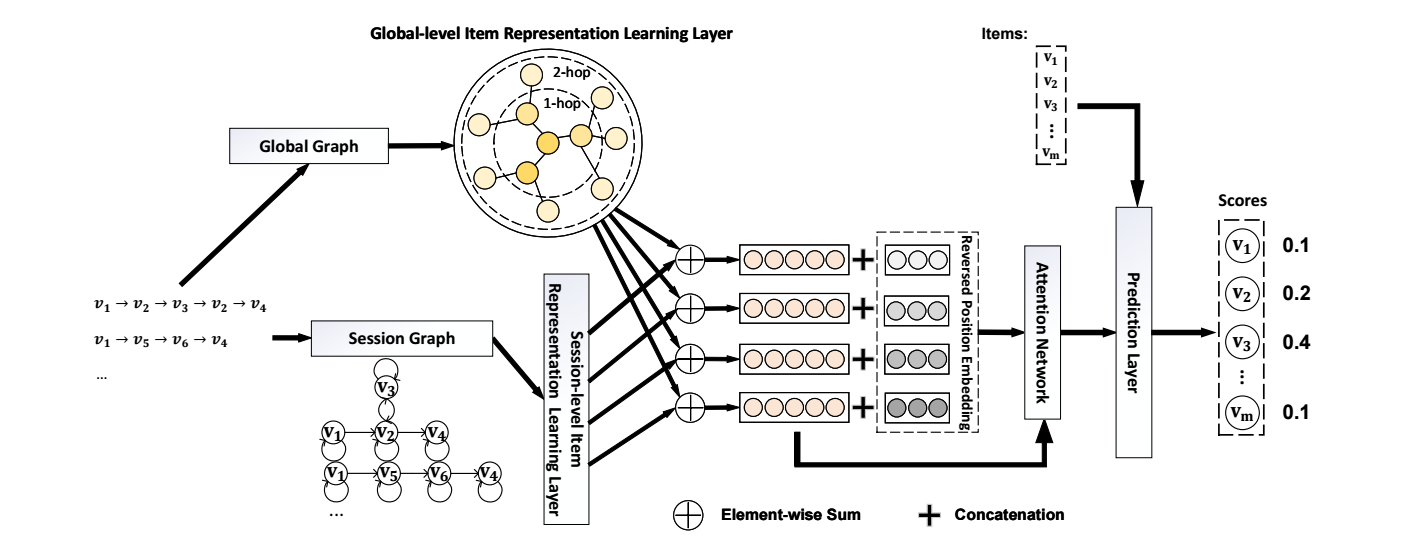
Global-level
-
假设 \(\mathbf{h}_v\) 为结点 \(v\) 的初始 embedding, 'global-level' item embedding:
\[\mathbf{h}_{\mathcal{N}_{v_i}^g} = \sum_{v_j \in \mathcal{N}_{v_i}^g} \pi(v_i, v_j) \mathbf{h}_{v_j}. \] -
其中 importance weight \(\pi(v_i, v_j)\) 为
\[\pi'(v_i, v_j) = \mathbf{q}_1^T \text{LeakyReLU}(\mathbf{W}_1, [\mathbf{s} \odot \mathbf{h}_{v_j} \| w_{ij}], ) \\ \pi(v_i, v_j) = \frac{\exp(\pi(v_i, v_j))}{\sum_{v_k \in \mathcal{N}_{v_i}^g \exp(\pi(v_i, v_k))}}. \]\(\mathbf{W}_1, \mathbf{q}\) 为可训练的参数, \(w_{ij} \in \mathbb{R}^1\) 为 edge \((v_i, v_j)\) 的权重,
\[\mathbf{s} = \frac{1}{|S|} \sum_{v_i \in S} \mathbf{h}_{v_i}. \] -
最后, global-level embedding:
\[\mathbf{h}_{v}^g = \text{Relu}(\mathbf{W}_2[\mathbf{h}_v \| \mathbf{h}_{\mathcal{N}_v^g}]). \] -
至此, 我们完成了一层的聚合操作, 可以将该操作拓展到更高层:
\[\mathbf{h}_v^{g, (k)} = \text{agg}(\mathbf{h}_v^{(k-1)}, \mathbf{h}_{\mathcal{N}_v^g}^{(k-1)}). \]
Session-level
-
首先计算 node \(v_j\) 对于 \(v_i\) 的 importance:
\[e_{ij} = \text{LeakyReLU}(\mathbf{a}_{r_{ij}}^T (\mathbf{h}_{v_i} \odot \mathbf{h}_{v_j})), \: j \in \mathcal{N}_{v_i}^s. \]这里 \(\mathbf{a}_{r_{ij}}\) 为可训练的参数, \(r_{ij}\) 指代文中定义的 4 种类型: \(a_{in}, a_{out}, a_{in-out}, a_{self}\). 而这里的 \(\mathcal{N}_{v_i}^s\) 也是表示 \(v_i\) 的一阶矩阵 (可以是上面的任意一种关系).
-
令
\[\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{v_k \in \mathcal{N}_{v_i}^s} \exp( \text{LeakyReLU}( \mathbf{a}_{r_{ik}}^T (\mathbf{h}_{v_i} \odot \mathbf{h}_{v_k}) ) )}. \] -
于是 session-level embedding:
\[\mathbf{h}_{v_i}^s = \sum_{v_j \in \mathcal{N}_{v_i}^s} \alpha_{ij} \mathbf{h}_{v_j}. \]
Session Representation Learning Layer
-
接下来我们要融合 global, session-level 的信息.
-
首先,
\[\mathbf{h}_v^{g, (k)} = \text{dropout}(\mathbf{h}_v^{g, (k)}), \\ \mathbf{h}_v' = \mathbf{h}_v^{g, (k)} + \mathbf{h}_v^s. \] -
作者引入可学习的位置编码 \(\mathbf{P} = [\mathbf{p}_1, \mathbf{p}_2, \ldots, \mathbf{p}_l]\), 并得到:
\[\mathbf{z}_i = \text{tanh}(\mathbf{W}_3[\mathbf{h}_{v_i}' \| \mathbf{p}_{l - i + 1}] + \mathbf{b}_3), \]注意, 这里位置编码的序是反着的. 这是因为, 考虑到不同序列长度可能不一样.
-
然后:
\[\mathbf{s}' = \frac{1}{l}\sum_{i=1}^l \mathbf{h}_{v_i^s}', \]表达了 session 信息.
-
最后整个 session 的表示为:
\[\mathbf{S} = \sum_{i=1}^l \beta_i \mathbf{h}_{v_i^s}', \]其中
\[\beta_i = \mathbf{q}_2^T \sigma(\mathbf{W}_4 \mathbf{z}_i + \mathbf{W}_5 \mathbf{s}' + \mathbf{b}_4). \] -
得分预测可以通过如下方式得到:
\[\hat{\mathbf{y}_i} = \text{Softmax}(\mathbf{S}^T \mathbf{h}_{v_i}). \]


