STAMP: Short-Term Attention Memory Priority Model for Session-based Recommendation
概
session 推荐的经典之作.
符号说明
- \(S_t = \{s_1, s_2, \ldots, s_t\}, 1 \le t \le N\), 序列;
- \(V = \{v_1, v_2, \ldots, v_{|V|}\}\), items;
- \(X = \{\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_{|V|}\}\), embeddings;
Short-Term Memory Priority Model (STMP)
-
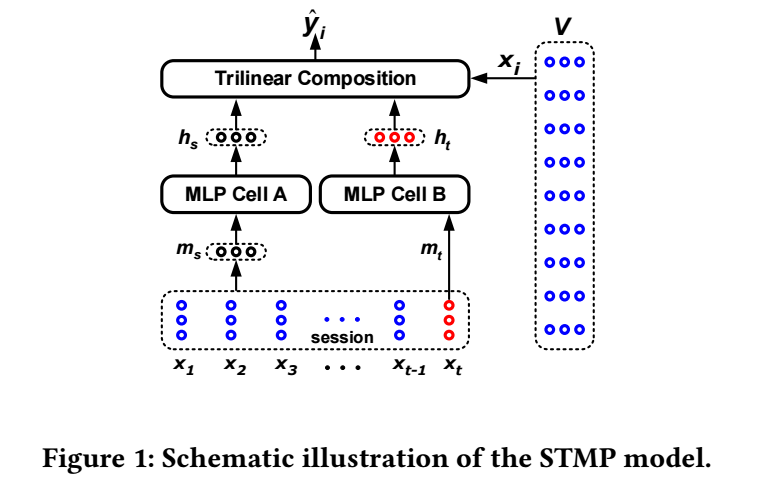
STMP 的结构如上图所示, 它主要包括两个部分:
- 序列中抽取兴趣: \(\mathbf{m}_s = \frac{1}{t} \sum_{i=1}^t \mathbf{x}_t\);
- 用户当前的兴趣: \(\mathbf{m}_t = \mathbf{x}_t\).
-
然后各自通过独立的 MLP 得到隐变量:
\[\mathbf{h}_s = f(\mathbf{W}_s \mathbf{m}_s + \mathbf{b}_s), \\ \mathbf{h}_t = f(\mathbf{W}_t \mathbf{m}_t + \mathbf{b}_t). \] -
最后通过, trilinear composition 得到最终的 score:
\[\hat{z}_i = \sigma(\sum_{j} [\mathbf{h}_s]_j \cdot [\mathbf{h}_t]_j \cdot [\mathbf{x}_i]_j), \quad i=1,2,\ldots, |V|. \] -
最后的通过 softmax \(\hat{\mathbf{y}} = softmax(\mathbf{z})\) 得到概率并通过如下的损失进行训练:
\[\mathcal{L}(\hat{\mathbf{y}}) = -\sum_{i=1}^{|V|} y_i \log (\hat{y}_i) + (1 - y_i) \log (1 - \hat{y}_i) \]
STAMP
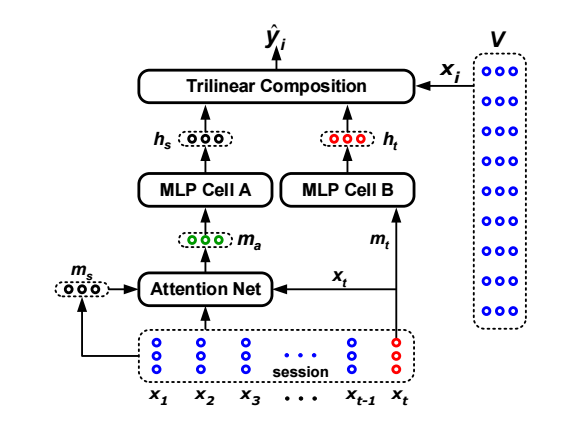
- STAMP 与 STMP 的区别在于对序列兴趣的建模之上: STMP 采用的是一种平均的方式, 而 STAMP 则利用了注意力机制:\[\mathbf{m}_a = \sum_{i=1}^t \alpha_i \mathbf{x}_i, \]其中每个结点的权重通过如下方式计算得到:\[\alpha_i = \mathbf{W}_0 \sigma(\mathbf{W}_1 \mathbf{x}_i + \mathbf{W}_2 \mathbf{x}_t + \mathbf{W}_3 \mathbf{m}_s + \mathbf{b}_a), \]其中 \(\mathbf{W}_0 \in \mathbb{R}^{1 \times d}, \mathbf{W}_1, \mathbf{W}_2, \mathbf{W}_3 \in \mathbb{R}^{d \times d}, \mathbf{b}_a \in \mathbb{R}^d\) 均为可训练的参数.


