Density estimation using Real NVP
Dinh L, Sohl-Dickstein J. and Bengio S. Density estimation using real nvp. ICLR, 2017.
概
一种可逆的 flow, 感觉很 diffusion 已经非常非常像了. 果然, 伟大的成果从来不是一蹴而就的.
Motivation
-
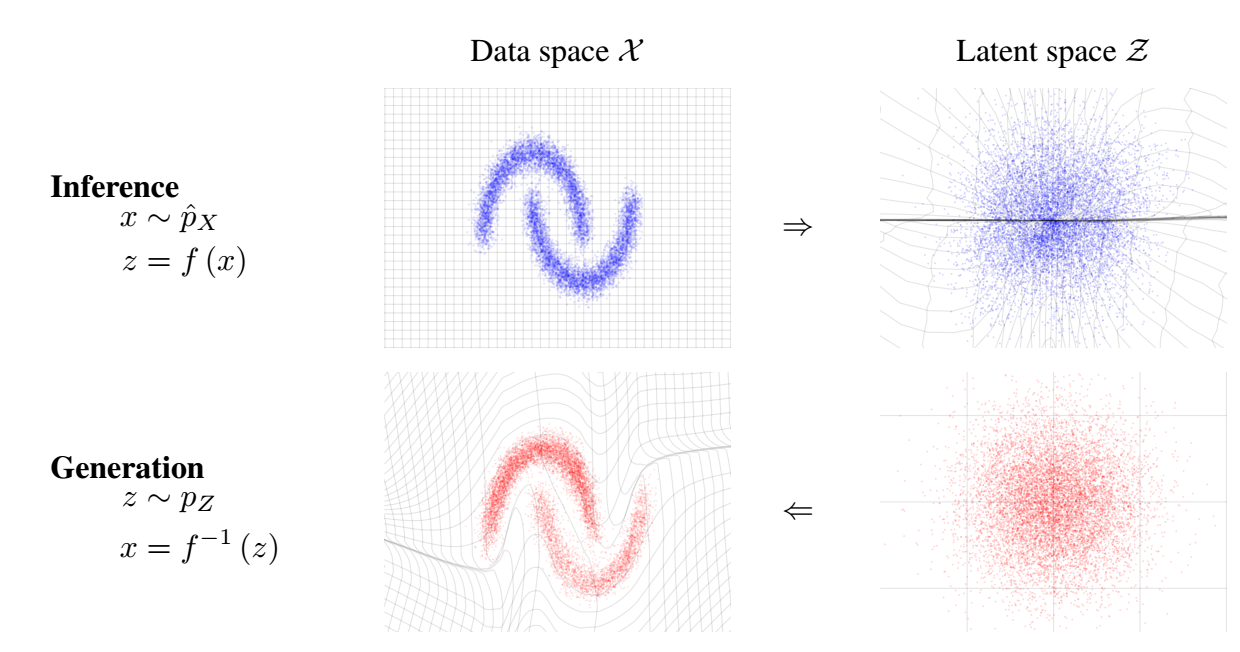
\(x\) 是原始数据, \(z\) 是隐变量, 作者希望找到一个可逆变换 \(f\) 满足:
- \(z = f(x)\) 服从一个简单的分布, 比如正态分布;
- 逆变换 \(f^{-1}\) 是容易操作的.
-
如此一来, 我们就可以直接从一个简单的分布 \(p_Z\) 中采样 \(z\), 然后通过
\[x = f^{-1}(z) \]就完成了 generation 的过程.
Real NVP
-
至于怎么找到这个变换 \(f(\cdot)\) 就是借用 flow 的思想了.
-
我们知道, 对于 \(z = f(x)\) 有
\[p_Z(z) = p_X(f^{-1}(z)) |\text{det}(\nabla_x f)|^{-1} \Rightarrow p_X(x) = p_Z(f(x)) |\text{det}(\nabla_x f(x))|. \] -
我们假设 \(p_Z(z)\) 服从一个简单的分布 (比如高斯分布), 如此一来只需要极大化对数似然即可:
\[\max_f \quad \log (p_X(x)) = \log (p_Z(f(x))) + \log (|\text{det}(\nabla_x f(x))|). \] -
整体的可行性要求:
- \(f(\cdot)\) 具有较强的表达能力, 使得它能够将 \(x\) 映射到一般的简单分布中去;
- \(\text{det}(\nabla_x f(x))\) 是容易求解的.
Coupling layers
-
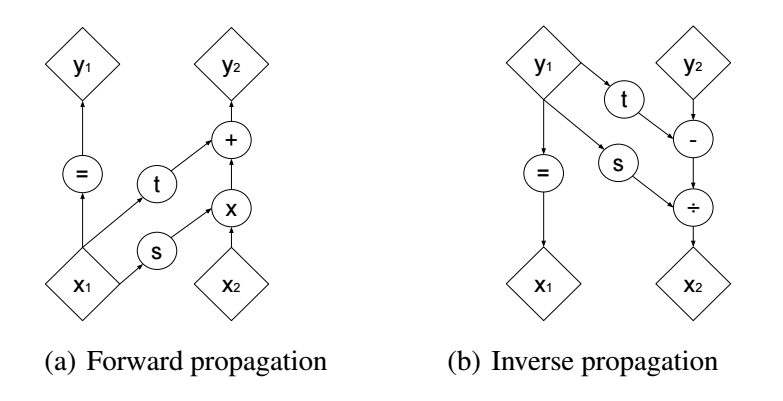
作者介绍了一种 coupling layers, 符合我们所需的条件.
-
每一层, 我们将输入 \(x\) 切分为 \([x_1, x_2]\), 然后根据如下变换得到输出:
\[y_1 = x_1 \\ y_2 = x_2 \odot \exp(s(x_1)) + t(x_1), \]其中 \(s, t\) 是可训练的 scale, translation function.
-
容易证明:
\[\nabla_x y = \left [ \begin{array}{ll} \mathbb{I}_d & 0 \\ \nabla_{x_1} y_2 & \text{diag}(\exp(s(x_{1:d}))) \end{array} \right ], \]为一下三角矩阵, 所以它的行列式就是对角元素的乘积.
-
如果给定 \(y\), 反向求解 \(x\) 也是容易的:
\[x_1 = y_1, \\ x_2 = (y_2 - t(y_1)) \odot \exp(-s(y_1)). \] -
假设我们用了两层:
\[z = f(y) = f \circ g (x), \]则
\[\nabla_x z = \nabla_y f \nabla_x g, \]故
\[\text{det}(\nabla_x z) = \text{det}(\nabla_y f) \text{det}(\nabla_x g), \]只需一层层算就可以了.
-
显然, 该思想可以很容易扩展到多层. 另外, 需要注意的是, 每一层, 输入的切分应当是各异的以避免一部分特征始终不变.
