Do Transformers Really Perform Badly for Graph Representation
概
本文提出了一种基于图的 Transformer 架构, 其中 centrality, spatial 和 edge encoding 经过了特殊的设计.
符号说明
- \(G = (V, E)\), 图;
- \(V = \{v_1, v_2, \ldots, v_n\}\);
- \(x_i\), node featuresl
- \(h_i^{(l)}\), 结点 \(v_i\) 在第 \(l\) 层的特征表示;
- \(\mathcal{N}(v_i)\), 结点 \(v_i\) 的一阶邻居;
Graphormer
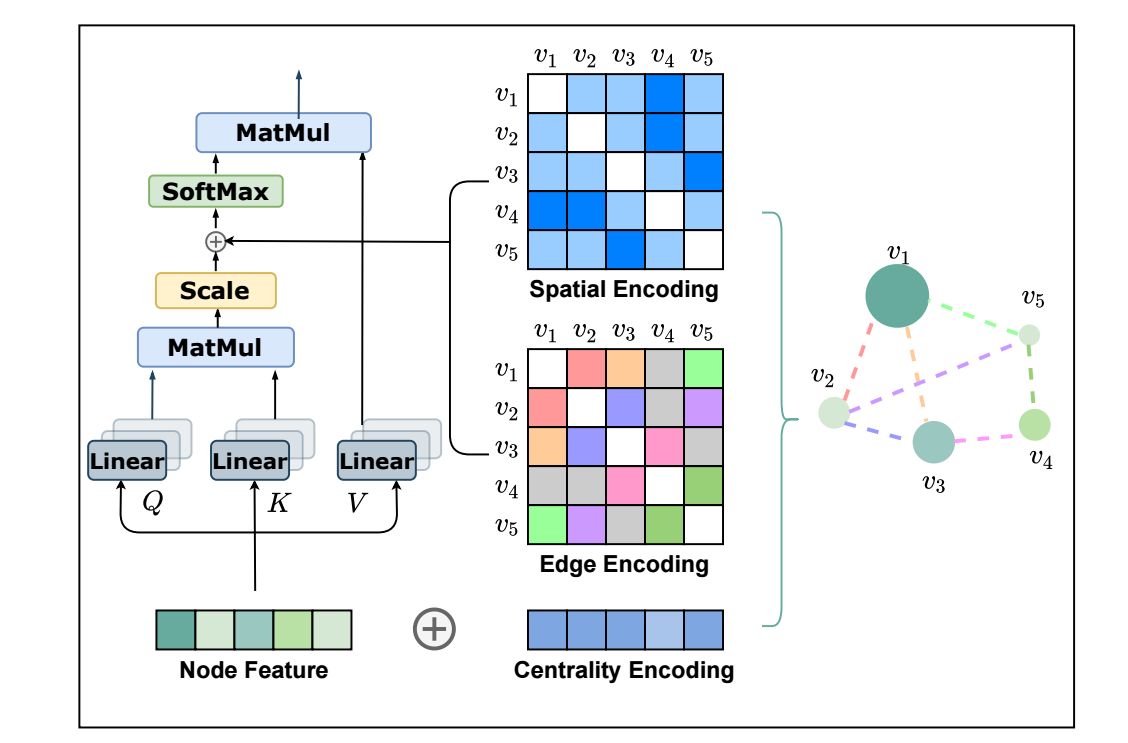
-
若上图所示, 在每一个计算 attention 的时候要加入 centrality, spatial, edge encodings 来帮助网络识别各结点和边的重要性.
-
Centrality Encoding: 在社交网络中, 名人 (即该结点的度数比较大) 往往会产生很大的影响, 所以, 实际中对于不同的结点我们应该考虑他们的度数的影响:
\[h_i^{(0)} = x_i + z_{\text{deg}^-(v_i)}^- + z_{\text{deg}^+(v_i)}^+, \]其中 \(z^-, z^+\) 分别式入度和出度所对应的 embeddings.
-
Spatial Encoding: 两个连接的结点, 由于其距离 (通过最短路径 \(\phi(v_i, v_j)\) 度量) 的不同, 关系的紧密也应当不同, 所以也应该将这部分信息融入进来. 如上图所示, 作者选择在计算 attention 的时候加入进来:
\[A_{ij} = \frac{(h_iW_Q)(h_j W_K)^T}{\sqrt{d}} + b_{\phi(v_i, v_j)}, \]其中 \(b_{\phi(v_i, v_j)}\) 是可学习的 bias, 融入了距离远近的信息.
-
Edge Encoding: 边的信息有写时候也是非常重要的, 假设 \((v_i, v_j)\) 的最短路径为 \(\text{SP}_{ij} = (e_1, e_2, \ldots, e_N)\), 作者通过如下方法引入 edge 信息:
\[A_{ij} = \frac{(h_iW_Q)(h_j W_K)^T}{\sqrt{d}} + b_{\phi(v_i, v_j)} + c_{ij}, \\ c_{ij} = \frac{1}{N} \sum_{n=1}^N x_{en} (w_n^E)^T, \]其中 \(x_{e}\) 为边 \(e\) 的特征 (连续特征 ?), \(w_n^E \in \mathbb{R}^{d_E}\) 为 n-th weight embedding.

