Understanding Structural Vulnerability in Graph Convolutional Networks

目录

• 概
• 符号说明
• 本文的方法
• 代码

Chen L., Li J., Peng Q., Liu Y., Zheng Z. and Yang C. Understanding structural vulnerability in graph convolutional networks. IJCAI, 2021.

概

mean 是在 GCN 中是一种常见的 aggregation 方式, 但是作者认为这种方式是不鲁棒的, 很容易受到异常连接的影响.

符号说明

• \(G = (V, E)\), 图;
• \(X_{v}\), node features;
• 一般的 GCN 的每一层可以表述为:
  \[a_v^{(k)} = f(\{h_u^{(k-1)}: u \in \mathcal{N}_v\}), h_v^{(k)} = \sigma(a_v^{(k)} W^{(k)}). \]
  其中 \(f\) 为 aggregation function.

本文的方法

• 这里省略本文的 motivation, 即关于 mean 不鲁棒的经验验证:

:

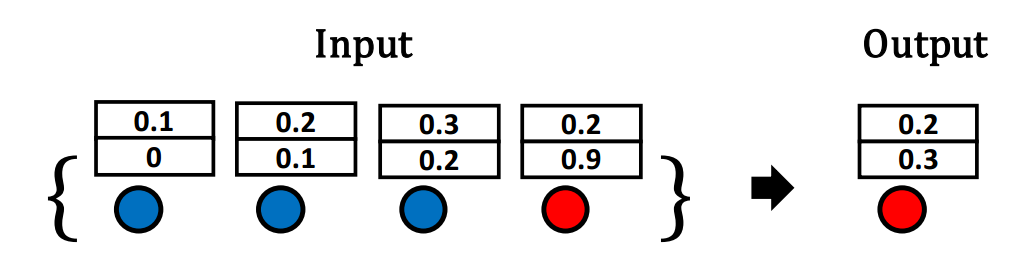• mean aggregation 可以表述为:

  \[a_v^{(k)} = \sum_{u \in \mathcal{N}_v} w_{uv} h_u^{(k-1)}, w_{uv} = \frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_v|}}. \]

• 作者提出用一下两种来替代:

  1. Median aggregation:

     \[a_v = \left \{ \begin{array}{ll} (h_{n / 2} + h_{(n / 2 + 1)}) / 2 & n \text{ is even}; \\ h_{(n+1) / 2} & n \text{ is odd}. \end{array} \right. \]

     即取中位数, 这里假设 \([h_u]_{u=1}^n\) 是有序的 (按照数值大小进行排序).

  2. Trimmed mean aggregation:

     \[a_v = \frac{1}{n - 2\lfloor n\alpha \rfloor} \sum_{u=s}^t h_u, s = \lfloor n\alpha \rfloor + 1, t = n - \lfloor n\alpha \rfloor, \]

     即该式只对 \([\alpha, 1 - \alpha]\) 内的取平均.

代码

official