Pairnorm tackling oversmoothing in gnns
Zhao L. and Akoglu L. Pairnorm: tackling oversmoothing in gnns. ICLR, 2020.
概
本文提出了一种 normaliztion 方法用于解决 over-smoothing 问题.
符号说明
- \(\mathcal{G} = (\mathcal{V}, \mathcal{E}, \mathbf{X})\), 图;
- \(\mathbf{X} = [\mathbf{x}_1, \ldots, \mathbf{x}_n]^T\), node features;
- \(\mathbf{D} \in \mathbb{R}^{n \times n}\), diagonal degree matrix;
- \(\mathbf{\tilde{A}} = \mathbf{A + I}\);
- \(\mathbf{\tilde{D}} = \mathbf{D + I}\);
- \(\mathbf{\tilde{A}}_{\text{sym}} = \mathbf{\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}}\).
- \(\mathbf{\tilde{A}}_{\text{rw}} = \mathbf{\tilde{D}^{-1}\tilde{A}}\).
PairNorm
-
一般的 GCN 的每一层 \(\mathbf{X} \rightarrow \mathbf{\bar{X}}\) 可以看成是下列问题的一步优化:
\[\text{min}_{\mathbf{\bar{X}}} \sum_{i \in \mathcal{V}} \|\mathbf{\bar{x}}_i - \mathbf{x}_i\|_{\mathbf{\tilde{D}}}^2 + \sum_{(i, j) \in \mathcal{E}} \|\mathbf{\bar{x}}_i - \mathbf{\bar{x}}_j\|_2^2, \]这里 \(\|\mathbf{z}\|_{\mathbf{\tilde{D}}}^2 = \mathbf{z}^T \mathbf{\tilde{D}}\mathbf{z}\).
-
可以发现, 上述损失最小化的过程实际上只需要要求 connected nodes 互相靠近就可以了. 显然是没有 disconnected nodes 原理的假设, 于是作者加上:
\[\text{min}_{\mathbf{\bar{X}}} \sum_{i \in \mathcal{V}} \|\mathbf{\bar{x}}_i - \mathbf{x}_i\|_{\mathbf{\tilde{D}}}^2 + \sum_{(i, j) \in \mathcal{E}} \|\mathbf{\bar{x}}_i - \mathbf{\bar{x}}_j\|_2^2 - \lambda \sum_{(i, j) \not \in \mathcal{E}} \|\mathbf{\bar{x}}_i - \mathbf{\bar{x}}_j\|_2^2. \] -
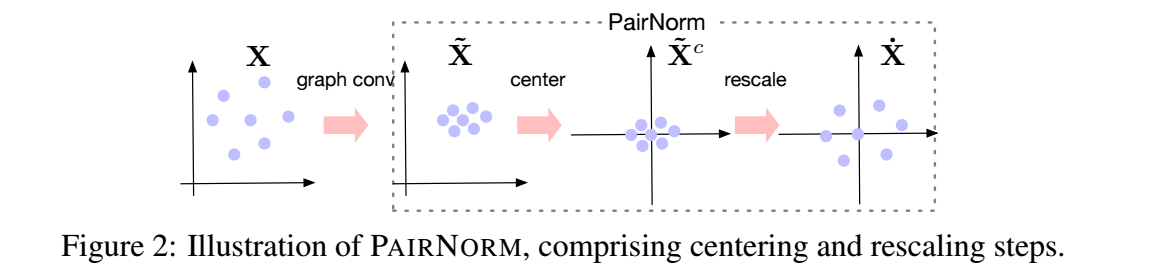
但是作者并没有去近似这个问题的解, 而是提出了 PairNorm 在每一层 normalize 它. 假设整个过程是 \(\mathbf{X} \rightarrow \mathbf{\tilde{X}} = \mathbf{\tilde{A}}_{\text{sym}}\mathbf{X} \longrightarrow \mathbf{\dot{X}} = \text{PairNorm}(\mathbf{\tilde{X}})\). 它希望标准化后的特征和上一层的特征 \(\mathbf{X}\) 间的 TPSD (total pairwise squared distance) 是一致的, 即:
\[\text{TPSD}(\mathbf{\dot{X}}) = \sum_{i, j \in [n]} \|\mathbf{\dot{x}}_i - \mathbf{\dot{x}}_j\|_2^2 = \sum_{i, j \in [n]} \|\mathbf{x}_i - \mathbf{x}_j\|_2^2 = \text{TPSD}(\mathbf{X}). \]
-
设想, 如果总的 TPSD 不变, 当相邻的近似的点互相靠近的时候, 不相邻的点就必须彼此远离.
-
为了避免 TPSD 不菲的计算量 (\(\mathcal{O}(n^2d)\)), 作者分两步走完成这一目标:
\[\mathbf{\tilde{x}}_i^c = \mathbf{\tilde{x}}_i - \frac{1}{n} \sum_{i=1}^n \mathbf{\tilde{x}}_i \\ \mathbf{\dot{x}}_i = s \cdot \frac{\mathbf{\tilde{x}}_i^c}{\sqrt{\frac{1}{n} \sum_{i=1}^n \|\mathbf{\tilde{x}}_i^c\|_2^2}} = s\sqrt{n} \cdot \frac{\mathbf{\tilde{x}}_i^c}{\sqrt{\|\mathbf{\tilde{X}}^c\|_F}}. \] -
容易发现, 此时:
\[\text{TPSD}(\mathbf{\dot{X}}) = 2n \|\mathbf{\dot{X}}\|_F^2 = 2n^2 s^2, \]为一常数.
-
此外, 作者还提出了一个 PairNorm-SI 的 normalization 方法:
\[\mathbf{\dot{x}}_i = s \cdot \frac{\mathbf{\tilde{x}^c_i}}{\|\mathbf{\tilde{x}_i^c\|_2}}, \]实际上就是每个 node features 都各自标准化了. emmm, 怎么说呢, 作者说这个版本效果会更好不就否定了之前的 motivation 吗?


