Towards Deeper Graph Neural Networks
Liu M., Gao H. and Ji S. Towards deeper graph neural networks. KDD, 2020.
概
本文介绍了一种加深模型的方法.
符号说明
- \(G = (V, E)\), 图;
- \(|V| = n\);
- \(|E| = m\);
- \(\bm{A} \in \mathbb{R}^{n \times n}\), 邻接矩阵;
- \(\bm{D} \in \mathbb{R}^{n \times n}\), diagonal degree matrx;
- \(\bm{X} \in \mathbb{R}^{n \times d}\), node feature matrix.
Motivation
-
图网络的每一层可以分解为:
- 邻居聚合:\[\bm{a}_i^{(l)} = \text{PROPAGATION}^{(l)} \Big( \{ \bm{x}_i^{(l-1)}, \{\bm{x}_j^{(l-1)}| j \in \mathcal{N}_i\} \} \Big), \]
- 特征变换:\[\bm{x}_i^{(l)} = \text{TRANSFORMATION}^{(l)} (\bm{a}_i^{(l)}). \]
- 邻居聚合:
-
之前的工作指出, 迭代很多层会导致 over-smoothing, 即所有的结点特征 \(\bm{x}_i^{(l)}, \bm{x}_j^{(l)}\) 随着 \(l\) 的加深会变得越来越无法区分.
-
作者首先定义两个结点间的相似度:
\[D(\bm{x}_i, \bm{x}_j) = \frac{1}{2} \|\frac{\bm{x}_i}{\|\bm{x}_i\|} - \frac{\bm{x}_j}{\|\bm{x}_j\|} \|, \]实际上就是 cosine 相似度.
-
由此, 我们可以定义某个结点的 smoothness:
\[SMV_i := \frac{1}{n-1} \sum_{j \in V, j \not= i} D(\bm{x}_i, \bm{x}_j). \] -
接着, 我们可以定义整个图上的 smoothness:
\[SMV_G = \frac{1}{n} SMV_i. \] -
作者首先对不同的层下的特征进行可视化, 如下图所示:
-
容易发现, 随着层数的加深, 的确是越来越无法区分.
-
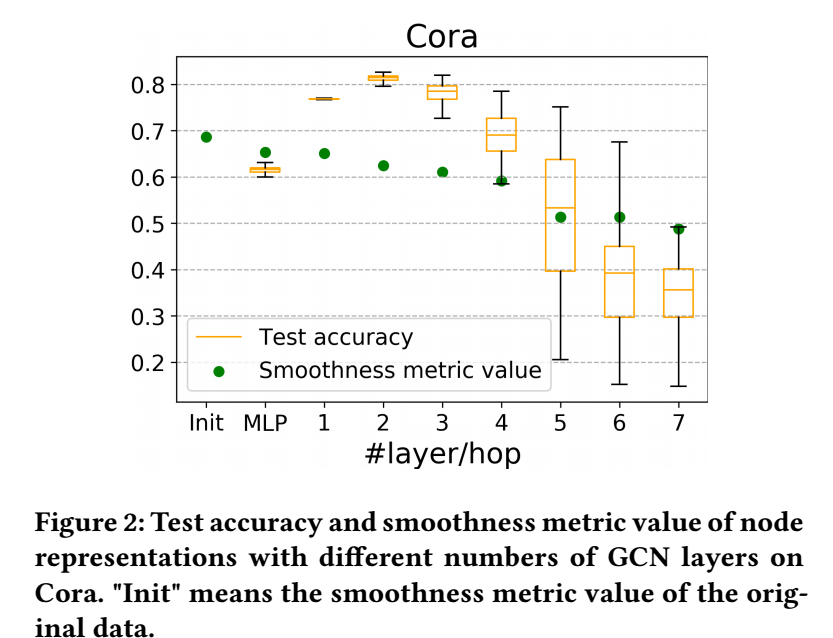
作者进一步比较不同层数下的 分类正确率 和 smoothness :
-
可以发现, smoothness 实际上并没有很快地收敛到 0 (根据 over-smoothing 的理论, 必然是很快地收敛到 0 的), 虽然在 4-5 层之间有一个明显的骤降.
-
作者认为是因为 邻居聚合 和 特征变换 互相交错导致的这个现象, 使得训练更加困难 (说实话, 逻辑很难直接串起来).
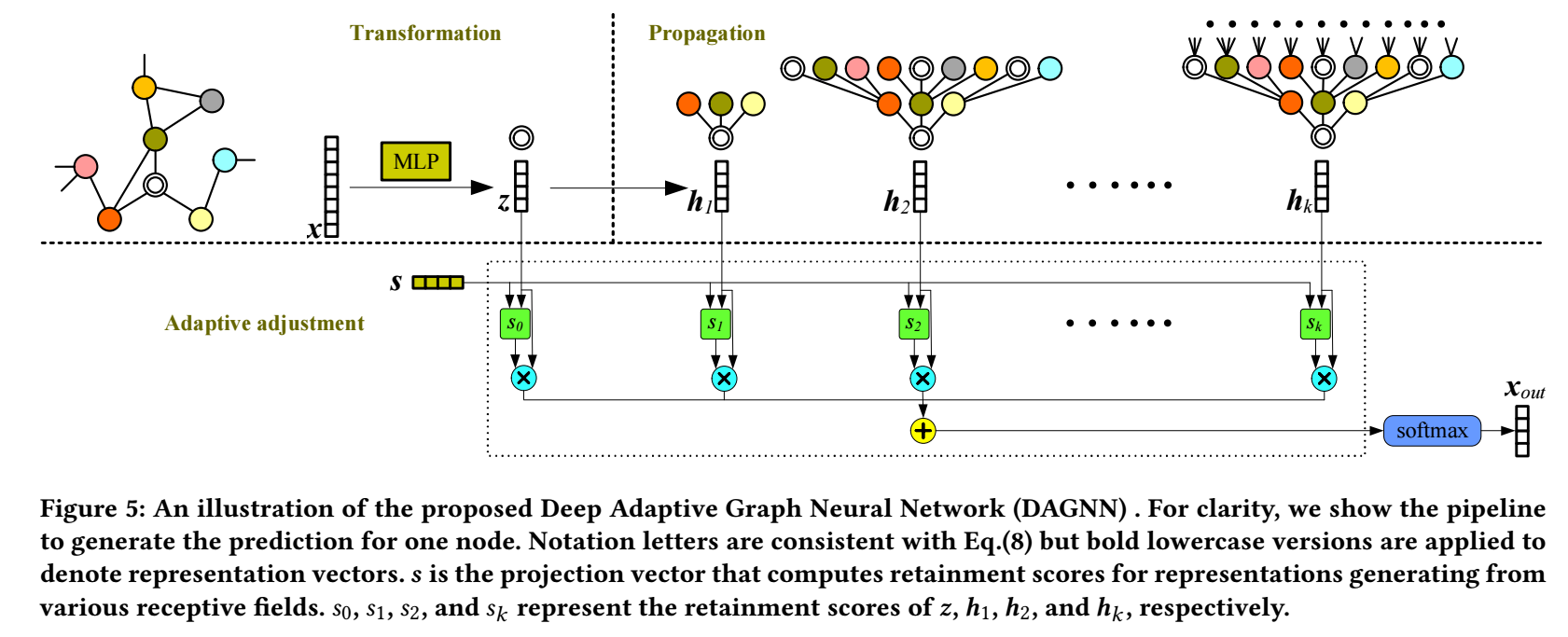
DAGCN
-
所以作者将两个过程解耦了.
-
首先通过
\[\bm{Z} = \text{MLP}(\bm{X}) \in \mathbb{R}^{n \times c} \]得到隐变量 \(\bm{Z}\).
-
接着, 利用邻居聚合得到:
\[\bm{H}_l = \hat{\bm{A}}^{l} \bm{Z}, \: l = 1, 2, \cdots, k. \]这里 \(\hat{\bm{A}}\) 是 normalized 邻接矩阵. 并令 \(\bm{H}_0 =\bm{Z}\).
-
为了统筹考虑不同层的特征, 作者设计了一个自适应权重, 每层的权重为:
\[\bm{w}_l = \sigma(\bm{H}_l \bm{s}) \in \mathbb{R}^{n}, l=0,1,\ldots, k. \]其中 \(\bm{s} \in \mathbb{R}^{c \times 1}\) 为可训练的参数.
-
于是, 最后的输出为:
\[\bm{X}_{out} = \text{softmax}\Big( \sum_{l=0}^k \text{diag}(\bm{w}_l) \bm{H}_l \Big) \in \mathbb{R}^{n \times c}. \] -
注意, 这里 \(c\) 是 node classes, 真的很奇怪.
