Diffusion models as plug-and-play priors
Graikos A., Malkin N., Jojic N. and Samaras D. Diffusion models as plug-and-play priors. NIPS, 2022.
概
有了先验分布 \(p(\mathbf{x})\) (用一般的扩散模型去拟合), 我们总是像添加一些约束, 即希望从条件概率分布 \(p(\mathbf{x}|\mathbf{y})\) 中采样. 作者在这里讨论的范围要更大, 只需给定一些约束 \(c(\mathbf{x}, \mathbf{y})\) 即可.
问题
-
假设我们对后验概率 \(p(\mathbf{x}|\mathbf{y}) \propto p(\mathbf{x}) c(\mathbf{x}, \mathbf{y})\) 感兴趣.
-
当 \(c(\mathbf{x}, \mathbf{y}) = p(y | \mathbf{x})\) 容易估计的时候, 这个问题是容易的 (这里我们假设先验分布 \(p(\mathbf{x}\)) 容易通过扩散模型近似).
-
但是当 \(c(\mathbf{x}, \mathbf{y})\) 本身不容易估计的时候, 这个问题会比较麻烦.
-
作者的想法是, 利用一个替代分布 (or variational posterior) \(q(\mathbf{x})\) 来近似 \(p(\mathbf{x}|\mathbf{y})\), 当然 \(q(\mathbf{x})\) 在形式上必须是容易采样和求解的.
-
需要注意的是, 虽然这里的符号是 \(q(\mathbf{x})\), 但是不意味着对于所有的 \(\mathbf{y}\) 都用同一个 \(q(\mathbf{x})\) 近似. 实际上, 真正的做法是, 对于每一条件 \(\mathbf{y}\) 求解一个替代分布 \(q(\mathbf{x})\), 所以实际上 \(q_{\mathbf{y}}(\mathbf{x})\) 或许更为贴切, 不过这里还是遵循此惯用用法.
-
一种简单的做法就是通过最小化 KL 散度:
\[\tag{1} \begin{array}{ll} \min_{q} \: \text{KL}(q(\mathbf{x}) \| p(\mathbf{x|y})) &= \int q(\mathbf{x}) \log \frac{q(\mathbf{x})}{p(\mathbf{x}|\mathbf{y})} \\ &\Leftrightarrow -\mathbb{E}_{q(\mathbf{x})} \Bigg [\log p(\mathbf{x}) + \log c(\mathbf{x}, \mathbf{y}) - \log q(\mathbf{x}) \Bigg] \\ &=: F. \end{array} \]最后的部分, 称为 variational free energy. 最小化 free energy 可以得到一个合适的近似. 注: variational free energy 又名 Evidence Lower Bound.
-
现在, 我们假设 \(p(\mathbf{x})\) 本身也是难以直接得到的 (正如扩散模型一下), 但我们可以直接的带 \(p(\mathbf{x}, \mathbf{h})\), 但是我们依旧只添加约束 \(c(\mathbf{x}, \mathbf{y})\), 此时 free energy 成为了:
\[\tag{2} \begin{array}{ll} F &= -\mathbb{E}_{q(\mathbf{x}) q(\mathbf{h}|\mathbf{x})} \Bigg [\log p(\mathbf{x}, \mathbf{h}) + \log c(\mathbf{x}, \mathbf{y}) - \log q(\mathbf{x})q(\mathbf{h}|\mathbf{x}) \Bigg] \\ &=-\mathbb{E}_{q(\mathbf{x}) q(\mathbf{h}|\mathbf{x})} \Bigg [\log p(\mathbf{x}, \mathbf{h}) - \log q(\mathbf{x})q(\mathbf{h}|\mathbf{x}) \Bigg] - \mathbb{E}_{q(\mathbf{x})} [\log c(\mathbf{x}, \mathbf{y})]. \end{array} \]
与扩散模型的联系
-
DDPM 拟合得到了如下的一个联合分布:
\[p(\mathbf{x}_T, \mathbf{x}_{T-1}, \ldots, \mathbf{x}_0) = p(\mathbf{x}_T) \prod_{t=1}^T p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t), \\ p_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \bm{\mu}_{\theta}(\mathbf{x}_t, t), \Sigma_{\theta}(\mathbf{x}_t, t)), \quad p(\mathbf{x}_T) = \mathcal{N}(\bm{0}, \mathbf{I}). \] -
令 \(\mathbf{x} = \mathbf{x}_0, \mathbf{h} = \mathbf{x}_{1:T}\):
- 首先, 根据扩散模型的性质我们可以知道得到:\[q(\mathbf{h}|\mathbf{x}=\mathbf{x}_0) = \prod_{t=1}^T q(\mathbf{x}_t|\mathbf{x}_{t-1}), \: q(\mathbf{x}_t|\mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}), \quad t=1,\ldots, T. \]
- 换言之, 我们需要估计仅仅是 \(q(\mathbf{x})\):\[\tag{3} \min_{q(\mathbf{x})} \quad F. \]
- 首先, 根据扩散模型的性质我们可以知道得到:
-
Ok, 让我们缓一缓, 其实扩散模型的损失和这里的损失是同一个, 只是扩散模型固定 \(q\) (2) 来训练 \(p_{\theta}\), 而现在是固定 \(p_{\theta}\) 来训练 \(q(\mathbf{x})\).
-
作者直接采用最简单的形式:
\[q(\mathbf{x}) = \delta(\mathbf{x} - \bm{\eta}), \]故 (3) 相当于:
\[\tag{4} \min_{\bm{\eta}} \quad F. \] -
进一步将 \(F\) 写成关于 \(\bm{\eta}\) 的形式:
\[F(\bm{\eta}) = \sum_t \mathbb{E}_{\bm{\epsilon} \sim \mathcal{N}(\bm{0}, \mathbf{I})} [\|\bm{\epsilon} - \bm{\epsilon}_{\theta}(\mathbf{x}_t, t)\|_2^2] - \log c(\bm{\eta}, \mathbf{y}), \: \mathbf{x}_t = \sqrt{\bar{\alpha}_t} \bm{\eta} + \sqrt{1 - \bar{\alpha}_t} \bm{\epsilon}. \] -
关于 \(\bm{\eta}\) 最小化 \(F(\bm{\eta})\) 即可:

-
考虑如下的优化:
\[\max_{\bm{\eta}} \int \delta(\mathbf{x} - \mathbf{\eta}) \log p(\mathbf{x}|\mathbf{y}) \mathrm{d}\mathbf{x} = \max_{\bm{\eta}} \: \log p(\mathbf{x}|\mathbf{y}), \]故
\[\mathbf{\bm{\eta}}^* = \arg\max p(\mathbf{x}|\mathbf{y}) \]实际上是 MAP 估计.
-
一个好处是, 我们不需要严格保证 \(c(\mathbf{x}, \mathbf{y}) = p(\mathbf{y}|\mathbf{x})\), 故严格上任意关于 \(\bm{\eta}\) 可导的函数都可以作为约束放在这里.
应用
条件采样
-
令 \(c\) 为 digit 的不同属性的 score (不用归一化):
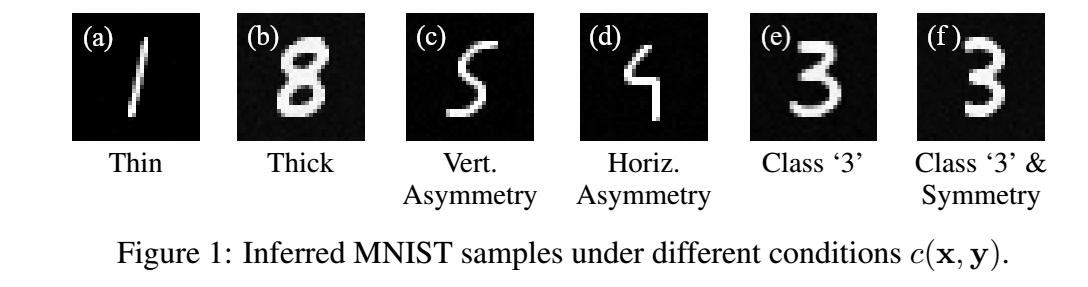
-
令
\[c(\mathbf{x}, \mathbf{y}) = \prod_{y \in \mathbf{y}} p(y | \mathbf{x}), \]其中 \(p(y|\mathbf{x})\) 是对 \(\mathbf{x}\) 不同属性的预测, 比如在人脸中: no beard, smiling, blond hair, male 等.

语义分割
- 没怎么看懂.
解决离散问题
- 没怎么看懂.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号