Understanding Dataset Difficulty with V-Usable Information
概
将 \(\mathcal{V}\)-information 用在判断数据集的难易程度上.
符号说明
-
请务必先了解 \(\mathcal{V}\)-information.
-
\(X, Y\) 为定义在样本空间 \(\mathcal{X, Y}\) 上的随机变量.
-
\(\mathcal{V} \subset \Omega = \{f: \mathcal{X} \cup \empty \rightarrow \mathcal{P}(\mathcal{Y})\}\).
-
predictive \(\mathcal{V}\)-entropy:
\[H_{\mathcal{V}}(Y) = \inf_{f \in \mathcal{V}} \mathbb{E}[-\log_2 f[\empty](Y)]. \] -
conditional \(\mathcal{V}\)-entropy:
\[H_{\mathcal{V}}(Y|X) = \inf_{f \in \mathcal{V}} \mathbb{E}[-\log_2 f[X](Y)]. \] -
\(\mathcal{V}\)-information:
\[I_{\mathcal{V}}(X \rightarrow Y) = H_{\mathcal{V}}(Y) - H_{\mathcal{V}}(Y|X). \]
SNLI
-
Stanford Natural Language Inference (SNLI) 自然语言推理的一个数据集, 每条样本包含一句子对: 前提 (premise) 和假设 (hypothesis). 然后我们要判断这前提和假设满足下列的三个关系中的一个:
- E: entailment, 即由前提能够推出假设;
- N: neutral, 其它的情况;
- C: contradiction, 前提和假设存在矛盾.
-
比如如下的例子为 entailment 的例子:
- Women enjoying a game of table tennis.
- Women are playing ping pong.
DWMW17
- DWMW17 是一个仇恨发言的检测任务.
实际的应用
-
作者将比如 BERT, GPT2 等模型作为 \(\mathcal{V}\), 然后在给定的数据集上训练.
-
然后根据训练好的模型, 计算
\[H_{\mathcal{V}}(Y) = \mathbb{E}[-\log_2 g^*[\empty](Y)], \\ H_{\mathcal{V}}(Y|X) = \mathbb{E}[-\log_2 f^*[X](Y)]. \]于是 \(\mathcal{V}\)-information 也可以算出来.
-
首先要清楚的是, \(I_{\mathcal{V}}(X \rightarrow Y)\) 越大说明该数据集能够提供对指定的模型类型 \(\mathcal{V}\) 更有效的信息. 此时我们可以称该数据集: XXX-usable, 比如采用的是 BERT, 就可以说是 BERT-usable.
-
所以, 我们接下来讨论的数据集的难易程度, 实际上也是模型相关的, 严格来说, 我们只能称某个数据集对于某种架构的网络是困难的或者容易的.
不同的模型
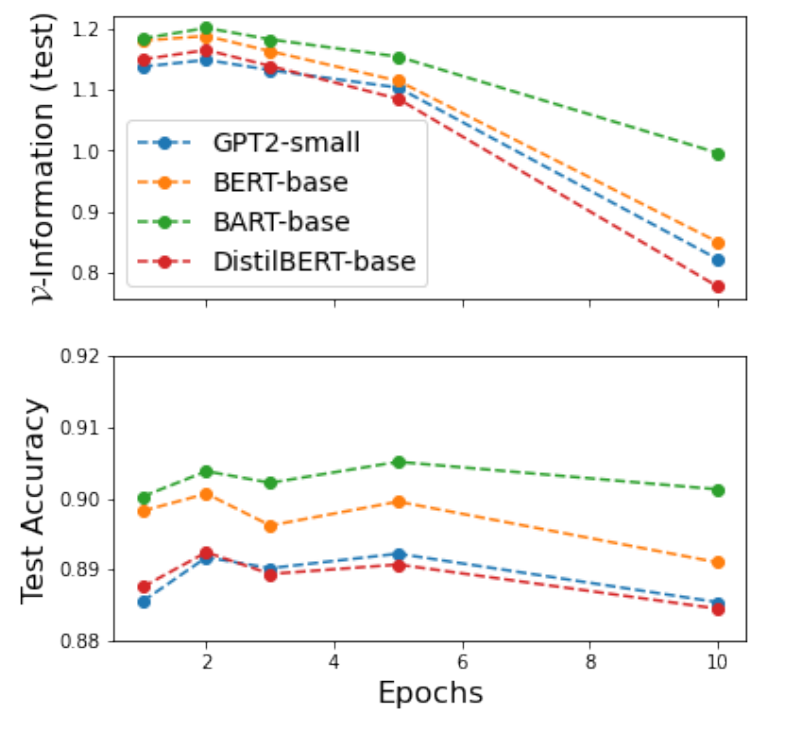
- 如上图所示, 我们可以得到如下的信息:
- \(\mathcal{V}\)-information 越大, 模型的正确率也越高, 二者是一致的;
- \(\mathcal{V}\)-information 对于 over-fitting 更加敏感.
Pointwise difficulty
-
有些时候, 我们更关注的不是数据集整体的难易程度, 而是数据集中那些样本是困难. 这一定程度上能够增加模型的可解释性 (了解模型在哪些样本上表现得更好或更差).
-
让我们定义 Pointwise \(\mathcal{V}\)-information (PVI):
\[\text{PVI}(x \rightarrow y) = -\log_2 g^*[\empty](y) + \log_2 f^*[x](y). \] -
故
\[I_{\mathcal{V}}(X \rightarrow Y) = \mathbb{E}_{x, y \sim \mathcal{P}(X, Y)} [\text{PVI}(x \rightarrow y)]. \] -
PVI 越大来说一般说明该样本对于某一种类型的模型来说越简单.
通过 PVI 找 mislabelled instances
- 上图列出了对于 BERT-base 来说 SNLI 中最难的几个样本, 标红的表示实际上该样本是 mislabelled 的.
错分的样本具有类似的 PVI
-
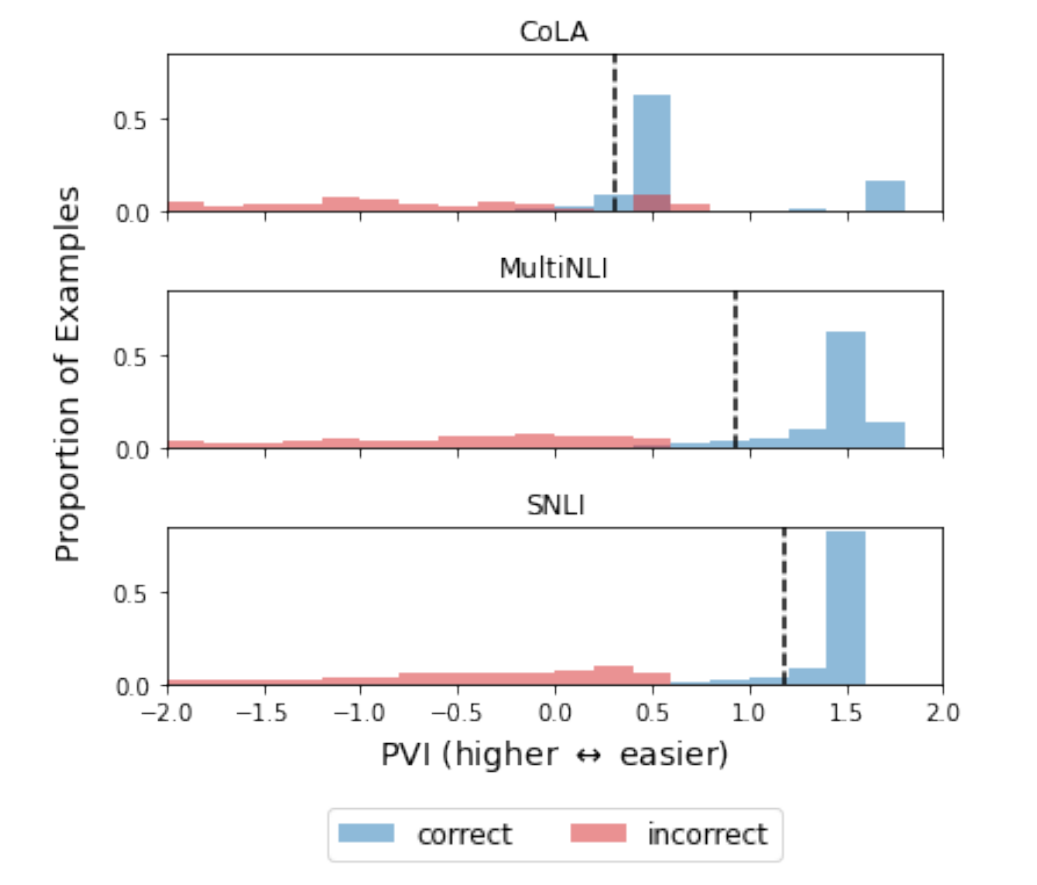
如上图所示, 在不同数据集上, 错分样本的 PVI 是接近 (\(<0.5\) bits).
-
暂时想不到有啥特别的应用场景, 不过倒是能说明这个方法的鲁棒性.
-
此外, 作者还做了相同数据集不同类型的模型, PVI 整体也是接近, 这也说明了该方法的一致性.
探索数据集中的重要部分
-
我们有些时候非常希望了解数据集哪些部分造成它是容易训练或者难以训练, 对于一般的评价指标这是很难做到的.
-
对于 \(\mathcal{V}\)-information \(I_{\mathcal{V}}(X \rightarrow Y)\) 而言, 我们可以将其改写一下:
\[I_{\mathcal{V}}(\tau(X) \rightarrow Y), \]这里我们把 \(\tau(\cdot)\) 看成是某种数据处理方法, 它会把原本数据中的某些信息抹去, 通过比较抹去前后的 \(\mathcal{V}\)-information 我们可以判断某类信息的重要性.
输入的变换
- 本文考虑了如下的几类变换:
- shuffled: 打乱语序, 用于判断序列信息的重要性;
- hypothesis-only: 只保留假设;
- premise-only: 只保留前提;
- overlap: 只保留同时出现在假设和前提中的词.
-
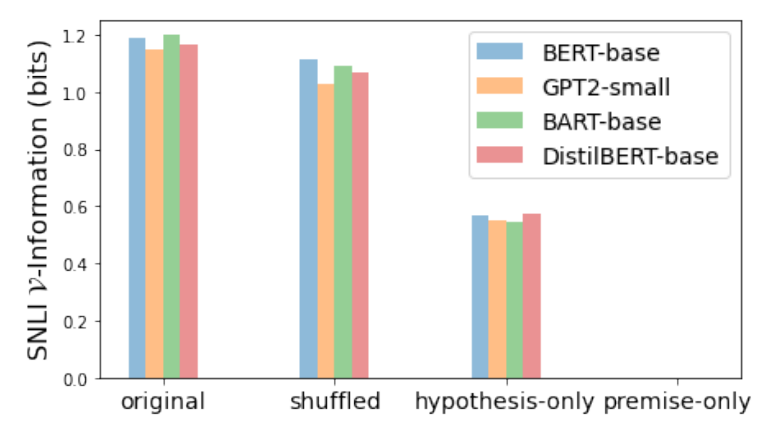
如上图所示, 我们可以发现:
- 对于 SNLI 而言, Token 本身提供了最多的信息, 序列提供了很少的信息;
- 前提 premise, 常常重复出现在多个样本实例中, 单独使用是没有多少价值的, 相反 假设, 由于它对于每个样本来说都是单独的, 所以更加有用.
-
对于 DWMW17, 倘若我们仅保留 50 个侵犯性的词汇, 我们发现, \(\mathcal{V}\)-information 相较于使用全部词汇的情况并没有特别多的下降 (0.724 -> 0.490).
Slicing datasets
- 我们可以通过将某一种类型的样本 PVI 的做平均得到这一中类型的数据集的信息量.
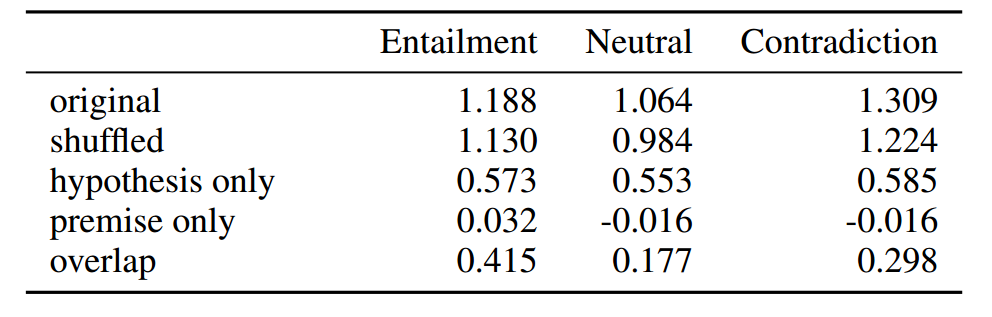
- 如上表所示, 仅保留前提和假设的重合的部分, 对于 entailment 已经能够提供相当的信息量, 但是对于 Neutral 和 Contradication 的情况则不行. 这是非常符合直觉的, 因为如果前提能够推出假设, 那么二者是耦合的也应当有更多的重合的部分.
Token-level
-
为了探究某一个 Token 对于整体的影响, 严格来说, 需要把该 token 从数据集中剔除, 然后重新训练模型. 如果想要探究每一个 token 的影响这计算代价显然是不能接受的.
-
所以作者退而求其次, 假设我们要考虑 token \(t\) 的影响, 作者利用如下公式估计:
\[\frac{1}{|\mathcal{D}_{C, t}|} \sum_{\mathcal{D}_{C, t}} \Bigg[ -\log_2 f^*[x_{\neg t}](y) + \log_2 f^*[x](y) \Bigg] \]其中 \(\mathcal{D}_{C, t}\) 表示仅包含类别 \(C\) 和 token \(t\) 的数据集.
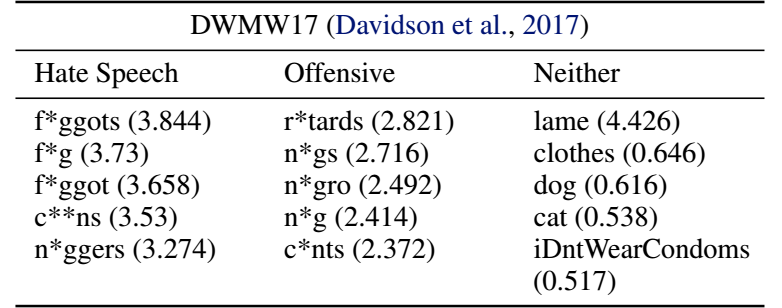
- 如上表所示, DWMW17 中种族和同性恋言论与仇恨言论的联系是最为紧密的.
