Handling Information Loss of Graph Neural Networks for Session-based Recommendation
概
作者发现图用在 Session 推荐中存在:
- lossy session encoding problem;
- ineffective long-range dependency capturing problem
的问题, 并给予解决.
符号说明
- \(G = (V, E)\), 图;
- \(s_i = [s_{i,1}, s_{i,2}, \ldots, s_{i,l_i}]\), session 序列.
存在的问题
Lossy session encoding problem
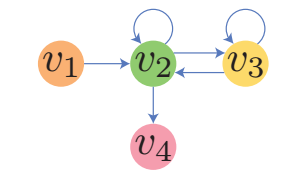
- 假设我们有两个序列: \([v_1, v_2, v_3, v_3, v_2, v_2, v_4]\) 和 \([v_1, v_2, v_2, v_3, v_3, v_2, v_4]\). 容易发现, 通过这两个序列构建的有向图是一样的 (如上图所示). 换言之, 我们无法通过有向图恢复出唯一的 session 序列, 由 session 序列到有向图的这一过程中存在信息丢失.
Ineffective long-range dependency capturing problem
- 由于 GNN 总是存在 over-smoothing 的问题, 所以往往最后的特征的感受野往往是很小的. 例如, 我们通常设置 layer 数目为 3, 此时感受野就是 3-hop 的. 但是对于序列推荐而言, long-range 的兴趣建模是很重要的.
LESSR
S2MG
-
作者利用 Session to EOP (edge-order preserving) Multigraph 来解决第一个问题.
-
Multigraph 的结点 \(u, v\) 间可能存在多个 transitions, 对于结点 \(v\), 我们假设 \(E_{in}(v)\) 为指向 \(v\) 的结点的列表 (按照连接的时间排列), 于是 session 序列 \([v_1, v_2, v_3, v_3, v_2, v_2, v_4]\) 可以转换成如下的图:
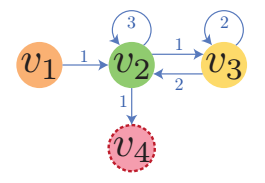
-
边上的权重是连接该点的序. 需要注意的是, 权重一词用在这里可能并不合适, 因为它仅仅代表序, 在 LESSR 的模型设计中, 也并没有将它作为权重来看待.
S2SG
-
作者利用 Session to Shortcut Graph 来解决第二个问题.
-
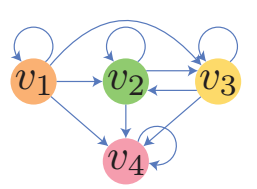
ShortCut graph 是一个无权有向图, 结点 \((u, v)\) 存在边当且仅当存在:
\[s_{i, t_1} = u, s_{i, t_2} = v, \: t_1 < t_2. \]于是 session 序列 \([v_1, v_2, v_3, v_3, v_2, v_2, v_4]\) 可以转换成如下的图:
模型
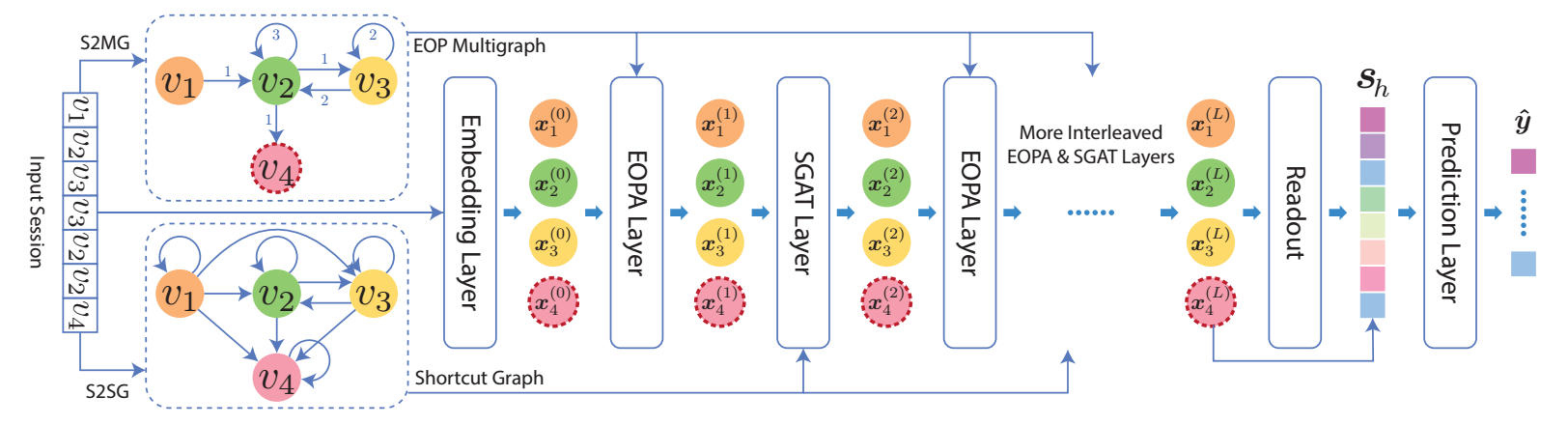
EOPA (Edge-Order Preserving Aggregation)
-
EOPA 在 EOP multigraph 上进行, 这里我们考虑对于 \(v_i\) 及其周围的邻居 \(E_{in}(i)\) 上的信息传播过程.
-
令 \(E_{in}(i) = [(j_1, i), (j_2, i), \cdots, (j_{d_i}, i)]\), 为有序列表, 则
\[\bm{x}_i^{(l+1)} = \mathbf{W}_{upd}^{(l)} (\bm{x}_i^{(l)} \| \bm{h}_{d_i}^{(l)}) \\ \bm{h}_k^{(l)} = \text{GRU}^{(l)} (\mathbf{W}_{msg}^{(l)}, \bm{x}_{j_k}^{(l)}), \bm{h}_{k-1}^{(l)}), \]这里 \(\|\) 表示连接操作.
SGAT (Shortcut Graph Attention)
- 为了进一步建模长期兴趣, 进一步利用 Shortcut graph, 它的传播过程如下:\[\bm{x}_i^{(l+1)} = \sum_{(j, i) \in E_{in}(i)} \alpha_{ij}^{(l)} \mathbf{W}_{val}^{(l)} \bm{x}_j^{(l)} \\ \bm{\alpha}_i^{(l)} = \text{softmax}(\bm{e}_i^{(l)}) \\ e_{ij}^{(l)} = (\bm{p}^{(l)})^T \sigma(\mathbf{W}_{key}^{(l)} \bm{x}_i^{(l)} + \mathbf{W}_{qry}^{(l)} \bm{x}_j^{(l)} + \bm{b}^{(l)}). \]这里 \(E_{in}(i)\) 是根据 Shortcut graph 得到的指向结点 \(i\) 的其它结点.
叠加
-
最后, 如上图所示, 作者把这些层重复叠加多次.
-
最后的全局特征表示为:
\[\bm{s}_g = \bm{h}_G = \sum_{i \in V} \beta_i \bm{x}_i^{(L)} \\ \bm{\beta} = \text{softmax}(\bm{\epsilon}) \\ \epsilon_i = \bm{q}^T \sigma(\mathbf{W}_1 \bm{x}_i^{(L)} + \mathbf{W}_2\bm{x}_{last}^{(L)} + \bm{r}). \]其中 \(\bm{q}, \bm{r}, \mathbf{W}\) 都是可训练的参数.
-
最后的局部特征表示为:
\[\bm{s}_l = \bm{x}_{last}^{(L)}. \] -
最后的特征为:
\[\bm{s}_h = \mathbf{W}_h (\bm{s}_g \| \bm{s}_l). \]
注: 损失用的交叉熵.
代码
[official]


