Heterogeneous Deep Graph Infomax
概
本文介绍了异构图的一种无监督学习方法. 这里大体只贴一下异构图的概念, 本文的方法不会讲.
异构图
-
\(\mathcal{G} = (\mathcal{V, E})\), 图;
-
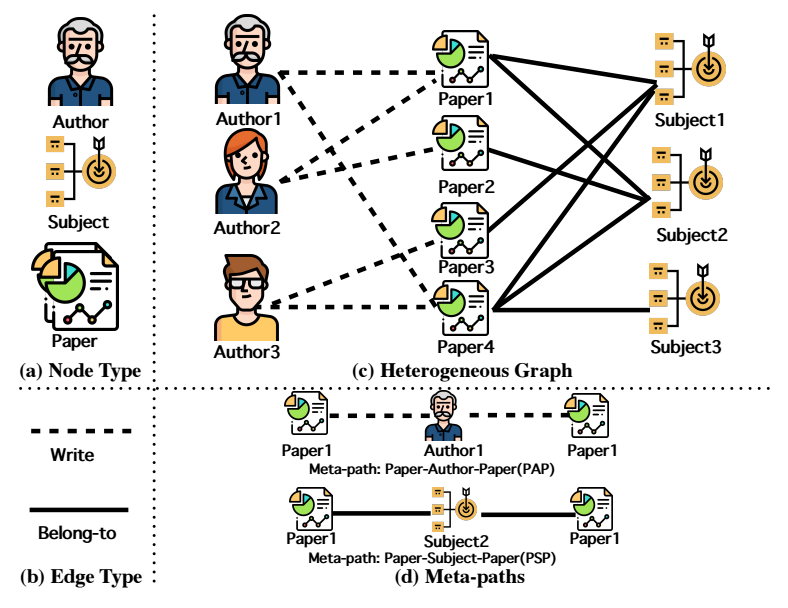
\(\phi: \mathcal{V} \rightarrow \mathcal{T}\), \(\phi(v)\) 返回结点 \(v\) 所属的类别, 如上图所示, 存在三种类型的结点 (即 \(|\mathcal{T}|=3\)): Author, Subject, Paper;
-
\(\psi: \mathcal{E} \rightarrow \mathcal{R}\), \(\psi(e)\) 返回边 \(e\) 所属的类别, 如上图所示, 存在两种类型的边 (即 \(|\mathcal{R}| = 2\)): Write, Belong-to;
-
显然, 一个图当且仅当 \(|\mathcal{T}| + |\mathcal{R}| > 2\) 的时候, 这个图才是异构图.
-
Meta-Path: Meta-Path 指的就是由一种结点类型到另一种结点类型的路径:
\[T_1 \mathop{\longrightarrow} \limits^{R_1} T_2 \mathop{\longrightarrow} \limits^{R_2} \cdots \mathop{\longrightarrow} \limits^{R_l} T_{l+1}, \]比如上图中, Paper-Author-Paper, Paper-Subject-Paper 都算是 meta-path. 需要注意的是, 在该论文的老的版本中, 并没有很准确的定义好 meta-path (其认为是结点到另一结点的路径即为 Meta-Path).
-
我们称结点 \(v_i, v_j\) 关于 meta-path \(\Phi\) 是相邻的, 若存在一路径为该 meta-path 的实例且连接这两个结点.
-
基于 \(\Phi\) 我们也可以推导出 meta-path based adjacency matrix \(A^{\Phi}\), 其中 \(A_{ij}^{\Phi} = 1\) 当且仅当 \(v_i, v_j\) 关于 \(\Phi\) 是相邻的.
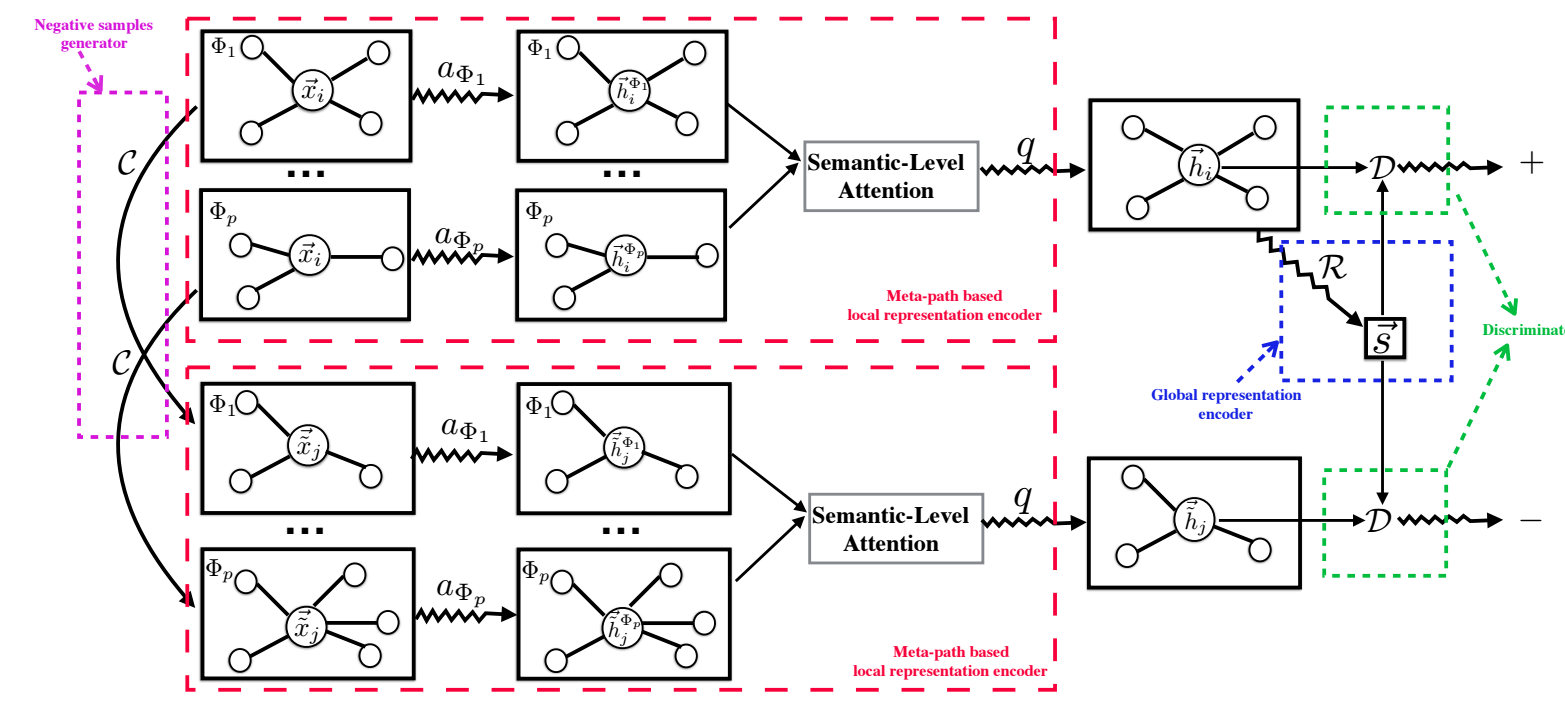
本文方法
