DiffuRec: A Diffusion Model for Sequential Recommendation
概
扩散模型用于序列推荐, 性能提升很大.
DiffuRec
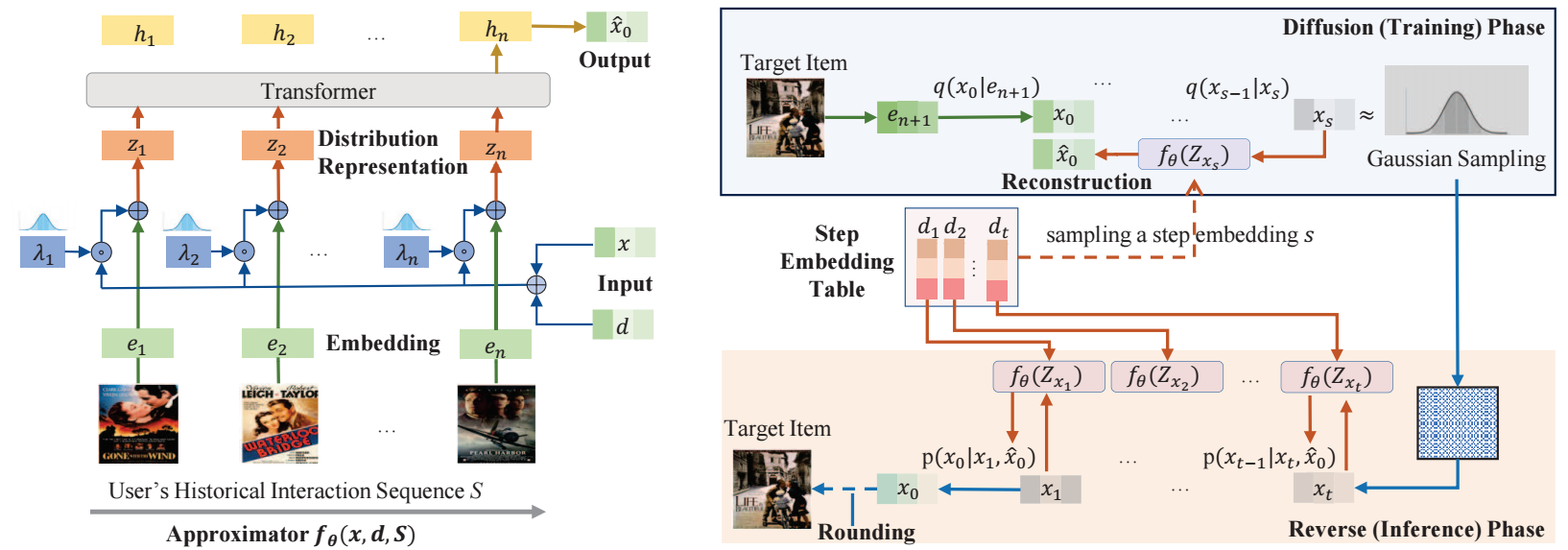
前向
- 前向和普通的扩散模型没有什么区别, 即\[\bm{x}_0 \mathop{\longrightarrow} \limits^{+\epsilon} \bm{x}_1 \mathop{\longrightarrow} \limits^{+\epsilon} \cdots \bm{x}_T \sim \mathcal{N}, \]不过采用的是 truncated linear schedule.
后向
- 后向是直接一步一步回来的, 并没有用 DDIM 加速, 所以 DiffuRec 的 timesteps 设的很小 \(=32\).
近似模型
-
与一般的扩散模型比较大的区别是模型的设置.
-
首先, 为每个 item 赋予一个 embedding \(\bm{e}_i\), 序列中扩散的任务是需要通过模型来拟合条件分布:
\[p(\bm{x}_{t-1}|\bm{x}_t, \{\bm{e}_j^u\}_{j=1}^n, t), \]其中 \(\{\bm{e}_j^u\}\) 表示用户的历史交互的 items.
-
作者的近似模型为:
\[\hat{\bm{x}}_0 = f_{\theta}(Z_x) = \text{Transformer}([\bm{z}_1, \bm{z}_2, \ldots, \bm{z}_n]) \\ \bm{z}_i = \bm{e}_i + \lambda_i \odot (\bm{x}_t + \bm{d}_t), \]即这是一个直接预测 \(\bm{x}\) 的模型. 在反向采样的过程中, 我们需要推断 \(\hat{\bm{x}}_{t-1}\), 这可以通过一定的变换得到.
-
在这里 \(\lambda\) 实际上控制了 '噪声' 的权重, 如果 \(\lambda=0\) 那 DiffuRec 就成了普通的序列推荐模型, 在这里 \(\lambda \sim \mathcal{N}(\delta, \delta)\). 实验中发现, \(\delta\) 需要足够小:
-
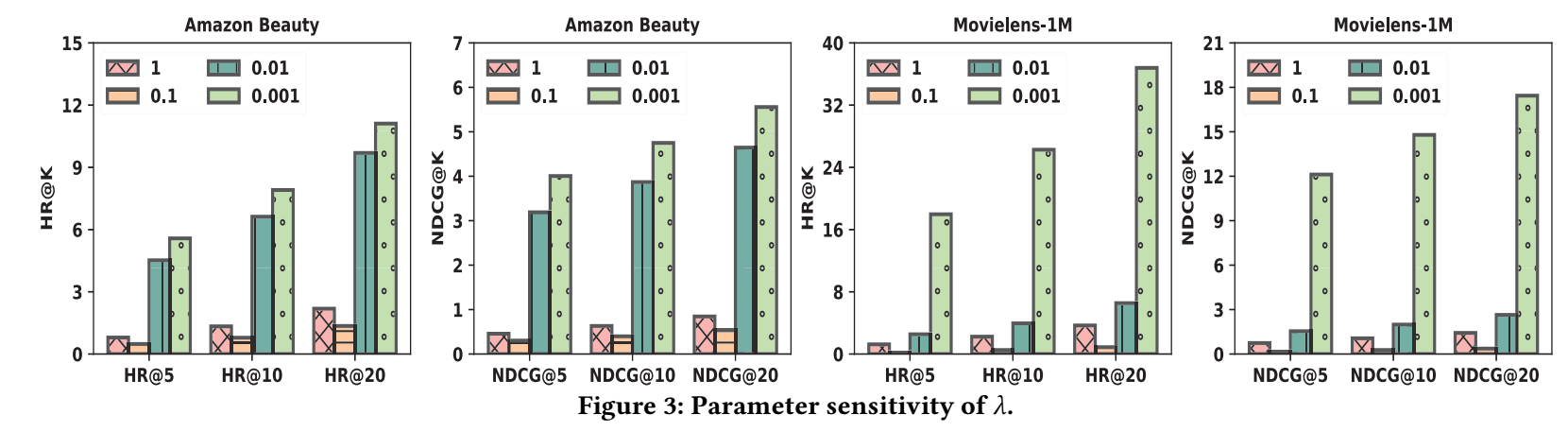
这是第一个让我感觉到有点奇怪的点.
-
此外, 不同于一般的扩散模型, 采用 MSE, 作者采用的是交叉熵
\[\mathcal{L}_{CE} = \frac{1}{|\mathcal{U}|} \sum_{i \in \mathcal{U}} -\log \hat{y}_i, \\ \hat{y} = \frac{\exp(\hat{\bm{x}}_0^T \bm{e}_{n+1})}{\sum_{i \in \mathcal{I}} \exp (\hat{\bm{x}}_0^T \bm{e}_i)}. \] -
这也是十分奇怪的一点, 因为这相当于完全破坏了 ELBO 的性质, 不是很理解.
-
最后, 采样得到的 \(\bm{x}_0\), 还需要通过 rounding 映射回到离散的空间中去:
\[\arg\max_{i \in \mathcal{I}} \: \bm{x}_0^T \bm{e}_i. \]
