Graph Neural Networks for Link Prediction with Subgraph Sketching
概
本文分析了原先的 MPNN 架构以及 subgraph GNN 在 link prediction 任务上的局限性, 以此提出了 ELPH (Efficient Link Prediction with Hashing) 用以结合二者.
符号说明
-
\(\mathcal{V}\), nodes;
-
\(\mathcal{E}\), edges;
-
\(G = (\mathcal{V, E})\), undirected graph;
-
\(d(u, v)\), shortest walk length;
-
\(S = (\mathcal{V}_S, \mathcal{E}_S)\), subgraph, 满足
\[\mathcal{E}_S = \{(u, v) \in \mathcal{E}| u, v \in \mathcal{V}_S\}. \] -
\(S_{uv}^k = (\mathcal{V}_{uv}, \mathcal{E}_{uv})\), 由边 \((u, v)\) 引出的 \(k\)-hop subgraph, 其中 \(\mathcal{V}_{uv}\) 是 \(u, v\) 的 \(k\)-hop neighbors.
必要的定义
同构与自同构-graph-level (\(G_1 \cong G_2\)): 假设 \(G_1 = (V_1, E_1), G_2 = (V_2, E_2)\) 为两个简单图, 称它们是同构的若存在一双射 \(\varphi: V_1 \rightarrow V_2\) 满足:
进一步, 若 \(G_1 = G_2\), 则称它们为自同构的.
直观上来讲, 两个图同构, 就是存在一一对应的点具有相同的结构.
G-自同构-node-level (\(u \sim_G v\)): 假设 \(G = (V, E)\) 为一简单图, \(u, v\) 为其中的两个点, 称它们是等价的若存在一双射 \(\varphi: V \rightarrow V\) 满足:
且
G-自同构-edge-level (\((u_1, v_1) \sim_G (u_2, v_2)\)): 假设 \(G = (V, E)\) 为一简单图, \((u_1, v_1), (u_2, v_2)\) 为其中的两条边, 称它们是等价的若存在一双射 \(\varphi: V \rightarrow V\) 满足:
且
Motivation
-
首先给出一个事实, 即 \(u_1 \sim_G u_2 \wedge v_1 \sim v_2 \not \Rightarrow (u_1, v_1) \sim_G (u_2, v_2)\), 如上图所示:
- 所有的点都是自同构的;
- 比如取 \(u_1 = u_2 = n_0, v_1 = n_1, v_2 = n_2\), 若 \((u_1, v_1) \sim_G (u_2, v_2)\), 则有 \((n_0, n_2) \in E\), 这是错的.
-
但是现在的 MPNN, 强调自己具有和 WL-Test 相当的表达能力, 恰恰意味着不能够很好地解决这个问题 (对于 link prediction 而言).
-
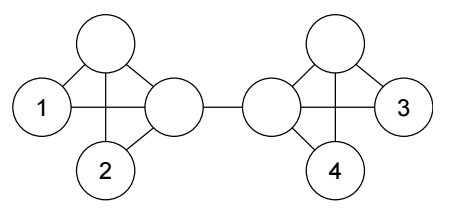
如上图所示, 依赖 WL 算法, 倘若我们连接 (1, 2), 那么必定也要连接 (1, 4):
-
因为倘若两个结点 \(v_2 \sim_G v_4\) 那么 WL 算法会为两个上同样的色, 可以看成是赋予相同的特征, 不妨设为 \(\bm{z}_2 = \bm{z}_4 = \bm{z}\);
-
此时, 一般的 link prediction 会通过:
\[s_{uv} = \phi(\bm{z}_u, \bm{z}_v) \]计算 score, 就会有
\[s_{12} = s_{14} = \phi(\bm{z}_1, \bm{z}). \] -
此时, 若 (1, 2) 被连接, 那么 (1, 4) 也应当被连接, 但是这和直观上的理解是不符的.
-
-
当然了, 需要说明的是, 上面的例子有其特殊性, 在实际中, 每个结点都有它的结点 (或者赋予 embedding), 这就导致实际上很难出现 \(\bm{z}_u = \bm{z}_v\) 的情况 (不考虑 over-smoothing).
-
现有的一些基于 subgraph 的方法通过为结点排序来解决这一问题 (见 Palette-WL, SEAL), 但是 subgraph 的提取是复杂的, 且不易并行计算.
ELPH
-
定义
\[\mathcal{A}_{uv}[d_u, d_v] := |\{n \in \mathcal{V}: d(n, u) = d_u, d(n, v) = d_v\}|, \\ \mathcal{B}_{uv}^k[d] := \sum_{d_v = k+1}^{\infty} \mathcal{A}_{uv}[d, d_v]. \] -
ELPH 的每一层为 (共 \(k\) 层):
\[\mathbf{e}_{u, v}^{(l)} = \{\mathcal{B}_{uv}[l], \mathcal{A}_{uv}[d_u, l], \mathcal{A}_{uv}[l, d_v] : \forall d_u, d_v < l\}, \\ \mathbf{x}_u^{(l)} = \gamma^{(l)} (\mathbf{x}_u^{(l-1)}, \Box_{v \in \mathcal{N}(u)}\Big\{ \phi^{(l)}(\mathbf{x}_u^{(l-1)}, \mathbf{x}_v^{(l-1)}, \mathbf{e}_{u, v}^{(l)}) \Big\} ), \]其中 \(\Box\) 是某种 permutation-invaiant aggregation function, 比如 (sum, mean, max). \(\mathbf{x}\) 是结点特征.
-
最后通过如下方式进行 link prediction:
\[p(u, v) = \psi(\mathbf{x}_u^{(k)} \odot \mathbf{x}_v^{(k)}, \{\mathcal{B}_{uv}[d]\}) \] -
总的来说, ELPH 既有 node features, 也有 'edge' features.
-
需要注意的是, 在实际中, \(\mathcal{A, B}\) 的计算是比较复杂的, 所以作者采用的是一种近似方法, 首先注意到:
\[\mathcal{A}_{u,v}[d_u, d_v] = |\mathcal{N}^{d_u}(u) \cap \mathcal{N}^{d_v}(v)| - \sum_{x \le d_u} \sum_{x \not= y \le d_v} |\mathcal{N}^x(u) \cap \mathcal{N}^y(v)|, \\ \mathcal{B}_{uv}^k[d] = |\mathcal{N}^d(u)| - \mathcal{B}^k_{uv}[d-1] - \sum_{i=1}^d \sum_{j=1}^d \mathcal{A}_{uv}[i, j], \]其中 \(\mathcal{N}^d(u) := \{v \in \mathcal{V}: d(v, u) \le d\}\). 注: 说实话, 我不是很能理解为什么 \(\mathcal{B}\) 有这样的迭代公式, 我自己推导出来的结果是:
\[\mathcal{B}_{uv}^k = |\mathcal{N}^d(u)| - |\mathcal{N}^{d-1}(u)| - \sum_{j=1}^k \mathcal{A}_{uv}[d, j]. \] -
注意, 即使如此, \(|\mathcal{N}^d(u)|\) 和 \(|\mathcal{N}^{d_u}(u) \cap \mathcal{N}^{d_v}(v)|\) 的计算依然是复杂的, 作者通过 MinHash 和 HyperLogLog 来近似它们.
-
通过 HyperLogLog 近似任意集合的大小 \(|S|\):
-
通过 MinHash 近似 Jaccard similarity.
