A Survey of Diversification Techniques in Search and Recommendation
概
本文对聚焦 diversity 的方法进行了一个回顾和总结. 这里主要记录一下评价多样性的指标.
符号说明
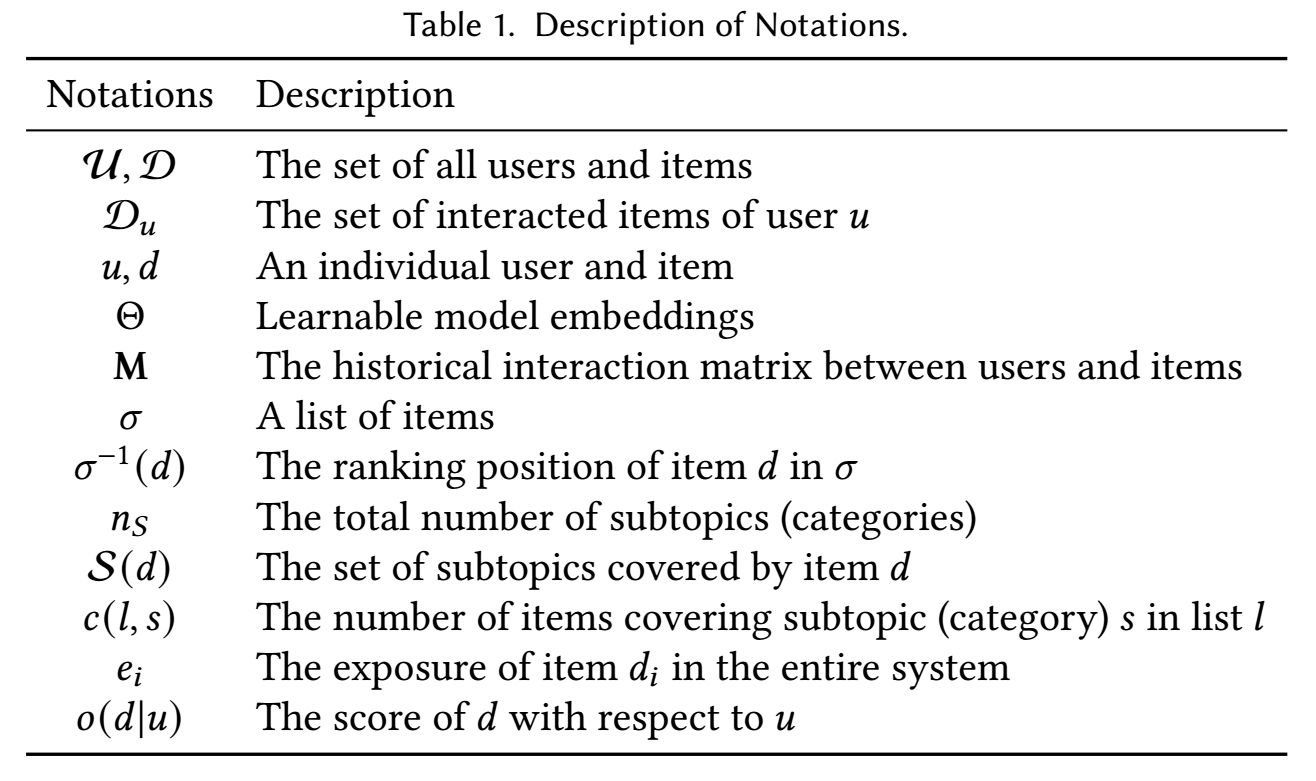
Diversity Metrics
Relevance-oblivious Diversity Metrics
Distance-based Metrics
-
ILAD \(\uparrow\) (Intra-List Average Distance):
\[\text{ILAD} = \mathop{\text{mean}} \limits_{d_i, d_j \in \sigma, i \not = j} \text{dis}_{ij}. \]其中 \(\text{dis}_{ij}\) 表示 \(d_i\), \(d_j\) 间的距离.
-
ILMD \(\uparrow\) (Intra-List Minimal Distance):
\[\text{ILAD} = \mathop{\text{min}} \limits_{d_i, d_j \in \sigma, i \not = j} \text{dis}_{ij}. \]
通过引入长度为 \(w\) 的滑动窗口可以将这些概念推广到 (local) 的概念:
-
ILALD \(\uparrow\) (Intra-List Average Local Distance):
\[\text{ILAD} = \mathop{\text{mean}} \limits_{\substack{ d_i, d_j \in \sigma, i \not = j \\ |\text{rank}(d_i|\sigma) - \text{rank}(d_j|\sigma)| \le w }} \text{dis}_{ij}. \]其中 \(\text{dis}_{ij}\) 表示 \(d_i\), \(d_j\) 间的距离.
-
ILMD \(\uparrow\) (Intra-List Minimal Local Distance):
\[\text{ILAD} = \mathop{\text{min}} \limits_{\substack{ d_i, d_j \in \sigma, i \not = j \\ |\text{rank}(d_i|\sigma) - \text{rank}(d_j|\sigma)| \le w }} \text{dis}_{ij}. \]
我们有如下几种方式来具体的定义 \(\text{dis}_{ij}\):
-
Cosine Diversity Distance. 假设我们拥有 item embeddings, 可以定义
\[\text{dis}_{ij} := 1 - \cos \langle d_i, d_j \rangle. \] -
Jaccard Diversity Distance. 我们也可以通过如下方式来定义:
\[\text{dis}_{ij} := \text{JDD}(d_i, d_j | u) = 1 - \frac{|\text{Expl}(u, d_i) \cap \text{Expl}(u, d_j)|}{|\text{Expl}(u, d_i) \cup \text{Expl}(u, d_j)|}, \]其中 (content-based strategy)
\[\text{Expl}(u, d) = \{d' \in \mathcal{D}| \text{sim} (d, d') > 0 \text{ and } d' \in \mathcal{D}_u\}, \]或 (collaborative filtering)
\[\text{Expl}(u, d) = \{u' \in \mathcal{U}| \text{sim} (u, u') > 0 \text{ and } d \in \mathcal{D}_{u'}\}. \] -
Gower Diversity Distance. 还可以定义为
\[\text{dis}_{i,j} := \text{GDD}(d_i, d_j) = \sum_k w_k \cdot \delta_k, \]其中 \(\delta_k\) 为两个 items 在 k-th 的属性差异, 而 \(w_k\) 是对应位置的权重 (感觉好复杂啊).
Converage-based Metrics
首先介绍 Rank-unaware 的方法, 这些大体是刻画推荐系统整体的多样性指标, 感觉目前我还用不到这些.
-
P-Coverage \(\uparrow\) (Prediction Coverage):
\[\text{P-Converage} = \frac{|\mathcal{D}_p|}{|\mathcal{D}|}, \]其中 \(\mathcal{D}_p\) 表示推荐的 (满足感兴趣条件的) items 的集合. 通常用来刻画推荐系统整体的多样性.
-
C-Converage \(\uparrow\) (Catalog Coverage):
\[\text{C-Coverage} = \frac{|\bigcup_{i=1}^N \sigma_i|}{|\mathcal{D}|}. \]刻画了所有推荐的 items 在整体的一个覆盖率. 同样是刻画系统整体的多样性.
-
S-Coverage \(\uparrow\) (Subtopic-Coverage):
\[\text{S-Coverage} = \frac{|\bigcup_{i=1}^N (\cup_{d \in \sigma_i} \mathcal{S}(d))|}{n_{\mathcal{S}}}, \]这里 \(\mathcal{S}(d)\) 表示 item \(d\) 所涵盖的 topic (或类别, 群体 ...), \(n_{\mathcal{S}} := |\bigcup_{d \in \mathcal{D}} \mathcal{S}(d)|.\)
接下来再介绍一些 Rank-aware 的尺度, 这些指标大抵是作用在一个推荐的 list 上, 需要注意的是, 这里的 Rank-aware 只是这些指标在不同的 Top-K 的推荐下会有不同的结果, 并非表示对于不同的 position 会有不同的权重.
-
S-RR@100% (Subtopic-Reciprocal Rank@100%):
\[\text{S-RR@100\%} = \min_k \Bigg( \Big| \bigcup_{i=1}^k \mathcal{S}(d_i) \Big| = n_{\mathcal{S}}. \Bigg) \]反应了为了覆盖所有的 topics 所需要推荐的 items 数.
-
S-Recall@K \(\uparrow\) (Subtopic-Recall@K):
\[\text{S-Recall@K} = \frac{|\cup_{i=1}^k \mathcal{S}(d_i)|}{n_{\mathcal{S}}}. \]反映了 Top-K 的推荐的覆盖率.
-
S-Precision@K \(\uparrow\) (Subtopic-Precision@K):
\[\text{S-Precision@K} = \frac{|\cup_{i=1}^k \mathcal{S}(d_i)|}{k}. \]
最后介绍 Social Welfare Metrics, 这些指标大抵是从一些别的领域 (经济等) 引用过来的, 个人感觉还是挺有意思的.
-
SD Index \(\downarrow\) (Simpson’s Diversity Index):
\[\text{SD Index} = \frac{ \sum_{i=1}^{n_S} [c(l, s_i) \cdot (c(l, s_i) - 1)] }{|l|(|l| - 1)}, \]其中 \(c(l, s_i)\) 表示 \(l\) 中包含 subtopic (或类别, 种类, 群体) \(s_i\) 的数目. 在每个 item 仅包含一个 subtopic 的情况下, 显然推荐的 items 不包含重复的 subtopics 时 SD Index 最小 (为 0).
-
Gini Index \(\downarrow\).
\[\text{Gini Index} = \frac{1}{2|\mathcal{D}|^2 \bar{e}} \sum_{i=1}^{|\mathcal{D}|} \sum_{j=1}^{|\mathcal{D}|} |e_i - e_j|. \]其中 \(e_i\) 表示 \(d_i\) 是否被推荐 ? \(\bar{e} = \frac{1}{|\mathcal{D}|}\sum_{i=1}^{|\mathcal{D}|} e_i\). 需要注意的是, Gini Index 是一个整体性的指标.
Relevance-aware Diversity Metrics
注: 虽然标题写着 relevance-aware, 但是所包括的指标中有些并没有把 relevance 考虑进来, 只是这些指标对于不同的 position 施加了不同的权重而已. 我不知道是否是我的理解有所差异.
Novelty-based Metrics
Novelty-based 的指标更关注我们推荐的 list 避免重复性.
-
\(\alpha\)-nDCG@K (Novelty-biased Normalized Discounted Cumulative Gain@K):
\[\text{Gain}(d_k) = \sum_{i=1}^{n_{\mathcal{S}}} \mathbb{I}[s_i \in d_k] (1 - \alpha)^{c(k, s_i)}, \\ \alpha \text{-DCG@K} = \sum_{k=1}^K \frac{1}{\log (k+1)} \cdot \text{Gain}(d_k). \]其中 \(c(k, s_i) = \sum_{j=1}^{k-1} \mathbb{I}[s_i \in d_j], \: c(0, s_i) = 0\). 进一步地, 我们可以计算 \(\alpha-\text{iDCG}@K\), 从而计算 \(\alpha\)-nDCG@K. 不过 \(\alpha-\text{iDCG}@K\) 是 NP-Complete 问题.
o -
NRBP (Novelty- and Rank-Biased Precision):
\[\text{NRBP} = \frac{1 - (1 -\alpha) \beta}{n_{\mathcal{S}}} \sum_{k=1}^{|\sigma|} \beta^{k-1} \sum_{i=1}^{n_{\mathcal{S}}} r(d_k|s_i) (1 - \alpha)^{c(k, s_i)}. \]其中 \(\beta\) 是认为给定的超参数, 它衡量了在浏览了当前 item 会继续浏览下一个 item 的概率. 所以 NRBP 实际上是一个期望收益.
-
nDCU@K (Normalized Discounted Cumulative Utility@K):
\[\text{DCU@K} = \sum_{k=1}^K \frac{1}{\log (k + 1)} \cdot \text{Utility}(d_k), \]其中
\[\text{Utility}(d_k) = \text{Gain}(d_k) - \text{Loss}(d_k). \]
Intent-aware Metrics
- 有些时候, 不同的 topic 的重要性是不同的, 但是上面的指标基本上是同等看待, 所以在有些时候是不妥的. 故 Intent-aware Metrics 此时就有了必要, 比如:\[\text{M-IA}(\sigma) = \sum_{i=1}^{n_{\mathcal{S}}} p(s_i|q) \cdot M(\sigma|s_i). \]其中 \(q\) 表示某个 query, \(M\) 可以是一些传统的指标, 比如: nDCG, MRR, MAP 等 (注意 \(|s_i\) 条件下, 不包含 \(s_i\) topic 的 items 应当看成是无关的 item).
