Practical Diversified Recommendations on YouTube with Determinantal Point Processes
概
本文利用 Determinatal Point Process (DPP) 来提高推荐 list 的多样性. 虽然是工业界的产物, 但是感觉还是挺好玩的.
Motivation
-
一般情况, 我们会用如下的方式
\[q_i \approx \mathbb{P}(y_i = 1| \text{features of item } i) \]来定义在某个 item 的质量 (quality), 其中 \(y_i = 1\) 表示产生交互 (比如被点击, 被购买) 行为.
-
但是往往相似的 items 具有相近的 quality. 反言之, 如果仅仅根据 quality 进行推荐, 容易重复地推荐类似的 items, 显然这不是一个好的策略. 所以, 在实际中我们还需要考虑推荐列表中物品的相似度, 这可以用如下方式来刻画, 如果 \((i, j)\) 满足
\[\mathbb{P}(y_i = 1, y_j = 1) \ll \mathbb{P}(y_i = 1) \mathbb{P}(y_j = 1), \]那么可以说 \((i, j)\) 是相似的, 互斥的. 因为上面的不等式说明 \((i, j)\) 是难以同时被选择的.
DPP
-
令 \(\mathcal{S} = \{1, 2, \ldots, N\}\) 表示所有的 items, 然后我们希望构造一个分布 \(\mathscr{P}\), 它定义在 \(S \subset \mathcal{S}\) 之上, 即给定任意 \(S \subset \mathcal{S}\),
\[\mathscr{P}(S) \]给出了选择 \(S\) 中的 items 的概率. 自然地, 应当满足:
\[\sum_{S \subset \mathcal{S}}\mathscr{P}(S) = 1. \] -
且为了满足上述的多样性的需求, \(\mathscr{P}\) 应当更加注重那些高质量但内部相似度较低的子集 \(S\).
-
假设我们已经预先设定了指标 \(L_{ij}\) 用于刻画 items \((i, j)\) 间的某种关系 (后续会介绍怎么构造是合理的), 则本文采用如下的分布的构造方案:
\[\mathscr{P}(Y) = \frac{\text{det}(L_Y)}{\sum_{S \subset \mathcal{S}} \text{det} (L_S) }. \] -
注意到, 行列式实际上行向量所构成的超平行多面体的体积 (here), 我们可以认为行列式越大, 那么所选的子集 \(Y\) 的'覆盖' 范围越大, 那么推荐效果越好.
-
举一个二维的例子:
\[L_Y = \left [ \begin{array}{ll} L_{11} & L_{12} \\ L_{21} & L_{22} \\ \end{array} \right ], \]有
\[\text{det}(L_Y) = L_{11} L_{22} - L_{12} L_{21}, \]如果 \(L_{11}, L_{22}\) 代表质量, \(L_{12}, L_{21}\) 代表相似度, 那么 \(\text{det}(L_Y)\) 越大说明 \(Y=\{1, 2\}\) 这一子集质量高, 多样性也好.
-
作者给出了两种策略用来构建 \(L\):
-
Kernel parameterization:
\[L_{ii} = q_i^2, \\ L_{ij} = \alpha q_i q_j \exp(- \frac{D_{ij}}{2 \sigma^2}), \: i \not = j. \]通过调节 \(\alpha\) 可以控制推荐尽可能小而美 (较大的 \(\alpha\)) 或者大而粗 (较小的 \(\alpha\)). 不过缺点是 \(\alpha\) 过大可能导致 \(L\) 不是半正定的, 此时需要我们每次重新将矩阵 project 到半正定的空间中去, 这不是一个好办法 (费时费力).
-
Deep Gramain Kernels 则是自动学习这样的一个矩阵:
\[L_{ij} = f(\bm{q}_i) \bm{g}^T(\phi_i) \bm{g}(\phi_j) f(\bm{q}_j) + \delta \mathbb{1}_{i=j}. \]大致流程如下:
-
-
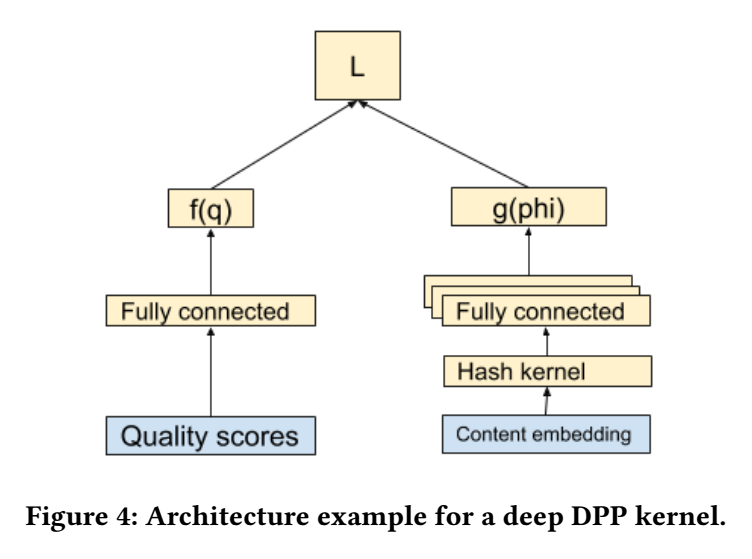
很容易发现, 在这种情况下搜索一个大小为 \(k\) 的子集是一个 NP-hard 的问题, 所以作者在实际上使用中是采用一种贪心算法. 即每次选择一个 item 使得
\[\mathop{\text{argmax}} \limits_{v \in \text{remaining videos}} \text{det}(L_{Y\cup v}). \]
注: 贪心算法其实不需要计算实际的概率, 不过我在论文中看到了一个很有趣的性质:
很有趣, 通过对角拆分应该是好证明的.
