Inductive Matrix Completion Based on Graph Neural Networks

目录

• 概
• 符号说明
• IGMC
  • Enclosing subgraph
  • Node labeling
  • Graph-level GNN
  • Optimization
• 代码

Zhang M. and Chen Y. Inductive matrix completion based on graph neural networks. In International Conference on Learning Representations (ICLR)

概

本文介绍了一种 Inductive 的矩阵补的方式, 作者主要用在推荐上.

注: 现在的图网络大体分为 transductive: 即要求测试的结点也在训练集中; inductive: 不要求测试的结点也在训练集中. 在推荐的场景中, 后者可以看成是解决冷启动问题的尝试.

符号说明

• $G = \langle U, V, E\rangle$, 二部图, 包含 user $u \in U$, item $i \in V$, 二者之间的边 $E$.
• $\mathbf{R} \in \mathcal{R}^{|U| \times |V|}$, rating matrix, 其中 $\mathcal{R}$ 表示 ratings 的种类, 比如 MovieLens 中有 $\mathcal{R} = \{1, 2, 3, 4, 5\}$.

IGMC

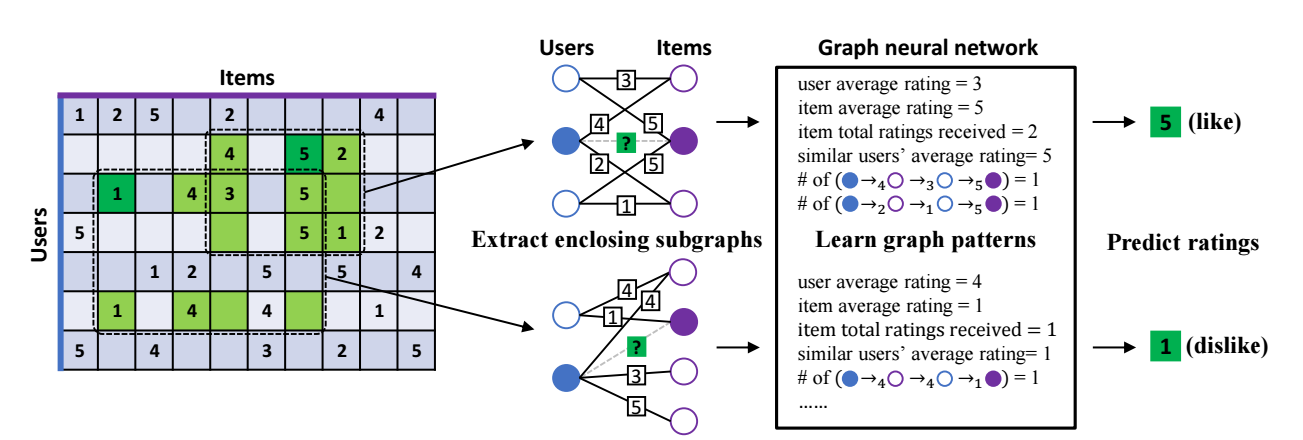
• IGMC 的主要流程是:
  1. 抽取基于 $(u, v)$ 的 1-hop enclosing subgraph;
  2. $1$-hop 结点编号;
  3. 喂入 graph-level 的 GNN 中进行编码;
  4. 利用分类器进行分类 (like/dislike).

Enclosing subgraph

• IMGC 的 link prediciton 是居于图的拓扑结构的, 也因此能够避免 ID 以及其它信息的需求.
• 作者采用如下算法抽取围绕 $(u, v)$ 的 h-hop enclosing subgraph (本文采用 $h=1$):
  

Node labeling

• 在喂入 graph-level 的 GNN 之前, 我们需要为采样出来的结点进行排序, 使得后续的 GNN 能够区分:

  1. user, item;
  2. 结点离目标结点 $(u, v)$ 之间的相对距离.

• 为此, 作者采取如下方式排序:

  1. 令 $u$ 的 label 为 0, $v$ 的 label 为 1;
  2. 假设结点 $n$ 为 user 且为 $i^{th}$-hop, 则其 label 为 $2i$;
  3. 假设结点 $n$ 为 item 且为 $i^{th}$-hop, 则其 label 为 $2i + 1$.

Graph-level GNN

• 接下来作者采用 R-GCN (relational graph convolutonal operator) 来提取特征, 其中的 message passing layer 为 (各层之间通过 Tanh 激活函数连接):

  $$\mathbf{x}_i^{l + 1} = \mathbf{W}_0^l \mathbf{x}_i^l + \sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}_r(i)} \frac{1}{|\mathcal{N}_r(i)|} \mathbf{W}_r^l \mathbf{x}_j^l.$$

  注意, 我们对不同的 $r \in \mathcal{R}$ 采用不同的权重矩阵 $\mathbf{W}_r$.

• 最后, 将各层的特征凭借起来得到新的特征表示:

  $$\mathbf{h}_i = \text{concat}(\mathbf{x}_i^1, \mathbf{x}_i^2, \ldots, \mathbf{x}_i^L),$$

  然后

  $$\mathbf{g} = \text{concat}(\mathbf{h}_u, \mathbf{h}_v).$$

• 最后, 通过下列分类器获得预测概率:

  $$\hat{r} = \mathbf{w}^T \text{ReLU}(\mathbf{Wg}).$$

Optimization

• 利用如下的 MSE 损失进行优化:

  $$\mathcal{L} = \frac{1}{|\{(u, v)| \mathbf{\Omega}_{u, v} = 1\}|} \sum_{(u, v): \mathbf{\Omega}_{u, v} = 1} (R_{u, v} - \hat{R}_{u, v})^2.$$

• 但是, 作者提出, R-GCN 为每个 $r \in \mathcal{R}$ 设置不同的权重矩阵 $W_r$. 但是直观上来说, $r=4, 5$ 往往表示喜欢, $r=1$ 往往表示不喜欢, 这种独立的做法不利于这种关系的学习. 故作者额外添加了如下的约束:

  $$\mathcal{L}_{\text{ARR}} = \sum_{i = 1, 2,\ldots, |\mathcal{R}| - 1} \|\mathbf{W}_{r_i+1} - \mathbf{W}_{r_i}\|_F^2.$$

• 最后的损失为:

  $$\mathcal{L}_{final} = \mathcal{L} + \lambda \mathcal{L}_{\text{ARR}}.$$

代码

official