LightGCL: Simple Yet Effective Graph Contrastive Learning for Recommendation
概
一种简单的图对比学习: 利用近似的 SVD 生成另一个 views.
符号说明
- \(u_i, v_j\), user, item, 分别有 \(I, J\) 个;
- \(\mathbf{e}_i^{(u)}, \mathbf{e}_j^{(v)} \in \mathbb{R}^d\), 对应的 embeddings;
- \(\mathbf{E}^{(u)} \in \mathbb{R}^{I \times d}, \mathbf{E}^{(v)} \in \mathbb{R}^{J \times d}\);
基本流程
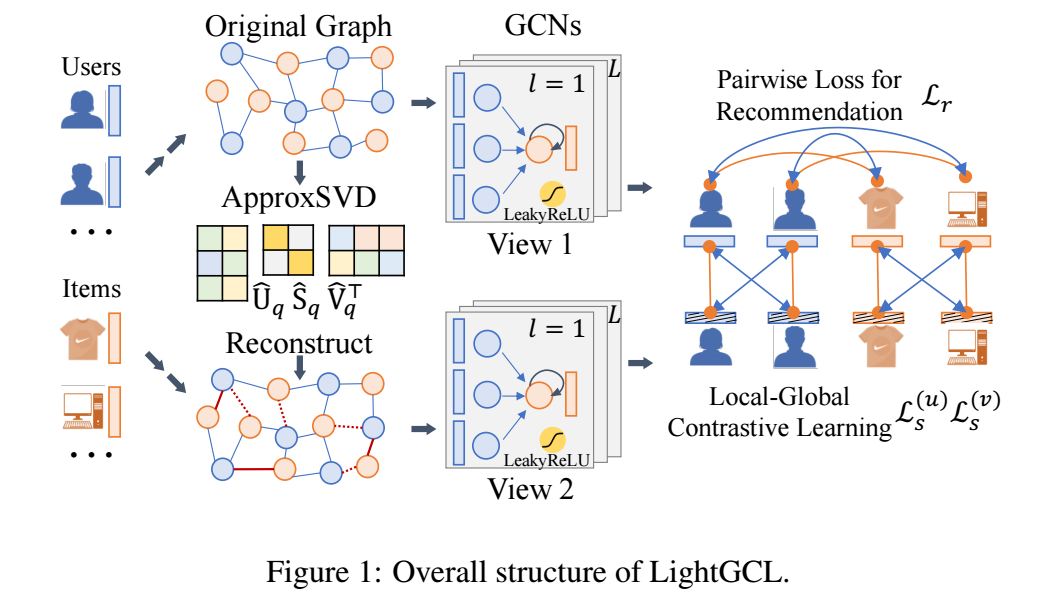
模型的基本流程
-
第 \(l\) 层经过如下的操作:
\[\mathbf{z}_{il}^{u} = \sigma( p(\tilde{\mathcal{A}}_{i, :}) \cdot \mathbf{E}_{l-1}^{(v)}), \quad \mathbf{z}_{j,l}^{u} = \sigma( p(\tilde{\mathcal{A}}_{:, j}) \cdot \mathbf{E}_{l-1}^{(u)}), \]其中 \(\tilde{A}\) 是'邻接'矩阵 (根据作者的描述, 实际上应该是交互矩阵), \(\sigma(\cdot)\) 表示 LeakyReLU (negative slope: 0.5). \(p(\cdot)\) 代表 edge dropout.
-
在每一层结束后, 还需要经过 residual connection:
\[\mathbf{e}_{i,l}^{(u)} = \mathbf{z}_{i,l}^{(u)} + \mathbf{e}_{i, l-1}^{(u)}, \quad \mathbf{e}_{j,l}^{(v)} = \mathbf{z}_{j,l}^{(v)} + \mathbf{e}_{j, l-1}^{(v)}. \] -
最后的特征表示为:
\[\mathbf{e}_i^{(u)} = \sum_{l=0}^L \bm{e}_{i, l}^{(u)}, \quad \mathbf{e}_j^{(v)} = \sum_{l=0}^L \bm{e}_{j, l}^{(v)}, \]然后通过内积计算 score:
\[\hat{y}_{i, j} = {\mathbf{e}_i^{(u)}}^T \mathbf{e}_j^{(v)}. \]
另一个 View
-
作者的想法是, 对邻接矩阵 \(\tilde{A}\) 做 (近似) 奇异值分解:
\[\tilde{A} \approx \hat{U}_q \hat{S}_q \hat{V}_q^T =: \hat{\mathcal{A}}. \] -
然后用该邻接矩阵得到另一个 View, 注意, 在实际上使用中, 并不会真的算出 \(\hat{\mathcal{A}}\), 而是
\[\mathbf{G}_l^{(u)} = \sigma(\hat{\mathcal{A}} \mathbf{E}_{l-1}^{(v)}) = \sigma(\hat{U}_q \hat{S}_q \hat{V}_q^T \mathbf{E}_{l-1}^{(v)}), \quad \mathbf{G}_l^{(v)} = \sigma(\hat{\mathcal{A}}^T \mathbf{E}_{l-1}^{(u)}) = \sigma(\hat{V}_q \hat{S}_q \hat{U}_q^T \mathbf{E}_{l-1}^{(u)}). \]因为 \(\hat{U}, \hat{V}\) 都是低秩的矩阵, 如果此一来我们不需要维护稠密的矩阵 \(\hat{\mathcal{A}}\), 且运算也更快.
优化
-
接下来只需要简单地运用 InfoNCE 损失即可:
\[\mathcal{L}_s^{(u)} = \sum_{i=0}^L\sum_{l=0}^L -\log \frac{\exp(s(\mathbf{z}_{i,l}^{(u)}, \mathbf{g}_{i,l}^{(u)}) / \tau)}{\sum_{i'=0}^L \exp(s(\mathbf{z}_{i,l}^{(u)}, \mathbf{g}_{i',l}^{(u)}) / \tau)}, \]即同一个结点为正样本对, 不同结点直接互为负样本对. 特别地, 作者每个 batch 都会利用 node dropout 来避免过拟合 (也就是说, LightGCL edge dropout 和 node dropout 都用了, 这么一看也不简单啊).
-
最后的总损失为:
\[\mathcal{L} = \mathcal{L}_r + \lambda_1 \cdot (\mathcal{L}_s^{(u)} + \mathcal{L}_s^{(v)}) + \lambda_2 \cdot \|\Theta\|_2^2, \\ \mathcal{L}_r = \sum_{i=0}^I \sum_{s=1}^S \max(0, 1 - \hat{y}_{i, p_s} + \hat{y}_{i, n_s}). \]


