Perception Prioritized Training of Diffusion Models
概
作者认为, 在 diffusion 过程中, \(\text{SNR}(t)\) 还比较小的时候给予更多权重去学习更有利于整体的学习, 遂提出了一种新的加权方法.
Motivation
-
前向:
\[q(\bm{x}_t|\bm{x}_{t-1}) = \mathcal{N}(\bm{x}_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t \bm{I}), \]则
\[q(\bm{x}_t|\bm{x}_0) = \mathcal{N}(\bm{x}_t; \sqrt{\bar{\alpha}_t} \bm{x}_0, (1 - \bar{\alpha}_t) \bm{I}), \\ \bar{\alpha} := \prod_{\tau=1}^t \alpha_{\tau}, \: \alpha_{\tau} := 1 - \beta_{\tau}. \] -
对于分布 \(\mathcal{N}(\mu, \sigma^2)\) 而言, 它的信噪比为:
\[\text{SNR} := \frac{\mu^2}{\sigma^2}, \]在概场景下, 前向的过程:
\[\text{SNR}(t) = \frac{\bar{\alpha}_t}{1 - \bar{\alpha}_t}, \]随着 \(t\) 的增加逐渐减小.
-
一般来说, DPM 中的 consistent term 为:
\[L_t = \mathbb{E}_{x_0, \epsilon} \Big[ \frac{(1 - \alpha_t)}{\alpha_t(1 - \bar{\alpha}_{t-1})} \|\epsilon_{\theta}(x_t, t) - \epsilon\|^2 \Big], \]然后总的损失为:
\[\mathcal{L}_{VLB} = \sum_t L_t. \] -
但是一般来说, 实际上用的是:
\[\mathcal{L}_{simple} = \sum_t \lambda_t L_t, \\ \lambda_t = \alpha_t (1 - \bar{\alpha}_{t-1}) / (1 - \alpha_t), \]这相当于把 MSE 前的系数都给去掉了. 当然, 这种损失虽然能够平衡方差, 让训练更加稳定, 但是也缺少学习的侧重性, 很难认为训练过程中所有的阶段都是同等重要的.
-
所以本文希望把 SNR 引入进来. 如下图所示 (注意, 横坐标 SNR 增加, 对应的 \(t\) 是减小的, 所以从生成的角度来说是从左往右的生成), \(\bm{x}_{tA}, \bm{x}_{tB}\) 源于同一个图片, \(\bm{x}_{tA}, \bm{x}_t'\) 来源于不同的图片, 随着图片的生成, 相同图片的更加近似, 而源于不同图片的两张图片会逐渐变得不同. 换言之, 在 SNR 很小的阶段, 图片需要学习更多的内容 (content), 那么自然地我们应该强调这一部分.
本文的方法
-
引入特殊的权重:
\[\lambda_t' = \frac{\lambda_t}{(k + \text{SNR}(t))^{\gamma}} \]于是最后的损失就成了:
\[\mathcal{L} = \sum_t \lambda_t' L_t. \] -
下图是在两种不同的 schedule 下的结果, 显然更加注重 content 部分的权重.
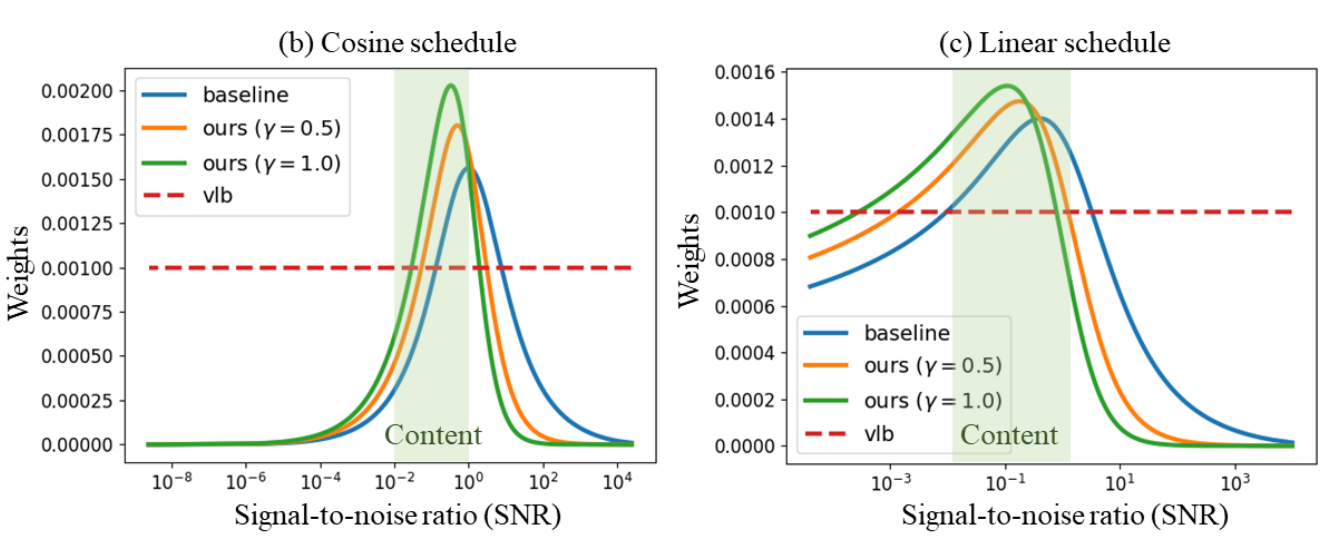
- 作者推荐是 \(k = 1, \gamma=1\).
