Diffusion-LM Improves Controllable Text Generation
概
本文介绍了一种将 DPM 应用到可控文本生成之上, 虽然 Text 的本质是离散的, 但是作者依然采用连续的方式进行扩散 (归功于所引入的 rounding 模块).
符号说明
- \(\mathbf{w} = [w_1, w_2, \ldots, w_n]^T \in \mathbb{R}^n\), words;
- \(p_{lm}(\mathbf{w})\), 普通的用于生成的语言模型;
- \(p(\mathbf{w}|\mathbf{c})\), 基于条件 \(\mathbf{c}\) 的语言生成模型 (比如, \(\mathbf{c}\) 可以是语法结构, 情感等);
流程
-
由于本文提出的条件生成模型是 classifier-guided 的, 所以就包含了两个单独的部分, 其中拟合 \(p(\mathbf{w})\) 如上图所示.
-
其整体的思路和原始的 DPM 并灭有特别的大差别, 主要需要解决的问题是:
-
前向的时候, 如何从离散的 Text (\(\mathbf{w}\)) 空间到连续空间? 作者给出的方案就是简单地用 embedding: 即首先 look_up 得到 embeddings:
\[\text{Emb}(\mathbf{w}) = [\text{Emb}(w_1), \ldots, \text{Emb}(w_n)] \in \mathbb{R}^{nd}, \]然后假设
\[q_{\phi}(\mathbf{x}_0|\mathbf{w}) = \mathcal{N}(\text{Emb}(\mathbf{w}), \sigma_0 I). \] -
后向的时候, 如何从连续的 \(\mathbf{x}_0\) 映射回离散的 Text 呢? 要知道, 几乎不可能 \(\mathbf{x}_0\) 恰好和某个词的 embedding 一致. 作者构建了可训练的 rounding step:
\[p_{\theta}(\mathbf{w}|\mathbf{x}_0) = \prod_{i=1}^n p_{\theta}(w_i | x_i), \]其中每个 \(p_{\theta}(w_i|x_i)\) 都是是通过 softmax 构建的.
-
-
在进行上述第二步的过程中, 作者遇到了些许麻烦, 虽然我没怎么看懂作者在这一刻的表述, 我感觉大概意思是在对齐方面出了些问题. 出问题的原因是 DPM 在 \(t=0\) 位置的训练不够, 所以作者直接添加了一个很强的 loss:
\[\sum_{t=1}^T \mathbb{E}_{x_t}\|f_{\theta}(\mathbf{x}_t, t) - \mathbf{x}_0\|^2. \] -
最后稍稍提一下条件生成的部分, 因为 DPM 采样只需要提供 \(p(\mathbf{x}_{t-1}|\mathbf{x}_t, c)\) 的梯度即可, 所以可以通过 (贝叶斯公式):
\[\nabla_{\mathbf{x}_{t-1}} \log p(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{c}) = \nabla_{\mathbf{x}_{t-1}} \log p (\mathbf{x}_{t-1}|\mathbf{x}_t) + \nabla_{\mathbf{x}_{t-1}} \log p(\mathbf{c}|\mathbf{x}_{t-1}). \] -
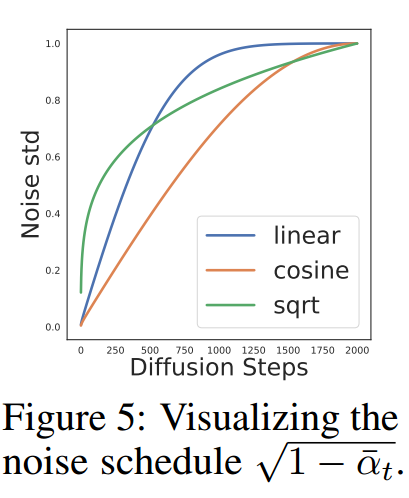
最后的最后提一个可能还挺重要的 trick, 正如之前所述, 作者认为在 \(t\) 接近 0 的附件拟合的不好, 所以作者希望更加强调这一部分, 所以采用的是一种新的 sqrt noise schedule:
\[\bar{\alpha}_t = 1 - \sqrt{t / T + s}, \]大概如下图所示:
