On the Theories Behind Hard Negative Sampling for Recommendation

概
符号说明
BPR 与 OPAUC
OPAUC 与 Top-K 指标
算法
代码

Shi W., Chen J., Feng F., Zhang J., Wu J., Gao C. and He X. On the theories behind hard negative sampling for recommendation. In International World Wide Web Conference (WWW), 2023.

概

本文把 pAUC 和推荐中一些常用的依赖 Top-K 的指标 (如, Recall, Precision) 联系在一起. 得出了:

倘若我们希望模型能够更加关注 K 更小的情况下的指标, 那么在训练过程中需要挑选更为复杂难度更大的负样本, 反之亦然.

虽然整体的思路或者是 Motivation 主要借鉴了 here, 但是其中的结论还是相当具有启发性的.

符号说明

\(c \in \mathcal{C}\), context, 如 user;
\(i \in \mathcal{I}\), item;
\(\mathcal{I}_c^+\), positive items for \(c\);
\(\mathcal{I}_c^- = \mathcal{I} \setminus \mathcal{I}_c^+\), negatives items for \(c\);
\(n_+ = |\mathcal{I}_c^+|, n_- = |\mathcal{I}_c^-|\);
\(r(c, i|\theta)\), score;
\(\mathcal{S}_{I_c^-}^{\downarrow}[1, M] \subset \mathcal{I}_c^-\), 表示负样本中按照 scores 降序排列的结果 (M 个);
BPR loss:
\[\min_{\theta} \: \sum_{c \in \mathcal{C}} \sum_{i \in \mathcal{I}_c^+} \mathbb{E}_{j \sim P_{ns}(j|c)} [\ell(r(c, i|\theta) - r(c, j|\theta))]. \]
其中 \(P_{ns}\) 代表某种采样策略.

BPR 与 OPAUC

我们知道:

\[TPR_{c, \theta} (t) = \mathbb{P}(r_{ci} > t | i \in \mathcal{I}_c^+), \\ FPR_{c, \theta} (t) = \mathbb{P}(r_{cj} > t | j \in \mathcal{I}_c^-). \\ \]
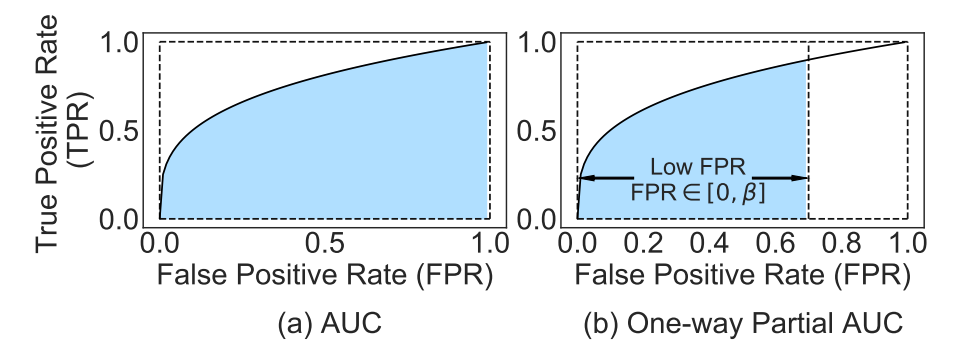
AUC 为二者所构成曲线内的面积, 即:

\[\text{AUC}(\theta) = \frac{1}{|\mathcal{C}|} \sum_{c \in \mathcal{C}} \int_0^1 TPR_{c, \theta} [FPR^{-1}_{c, \theta}(s)] ds = \mathbb{P}(r_{ci} > r_{cj}). \]

而 one-way partial AUC (OPAUC) 则是度量了在限定 FPR 在 \([\alpha, \beta]\) 条件下的面积 (特别地, 本文只考虑 \([0, \beta]\) 的情形):

\[\text{OPAUC}(\alpha, \beta; \theta) = \frac{1}{|\mathcal{C}|} \sum_{c \in \mathcal{C}} \int_\alpha^\beta TPR_{c, \theta} [FPR^{-1}_{c, \theta}(s)] ds = \mathbb{P}(r_{ci} > r_{cj}, r_{cj} \in [FPR^{-1}(\beta), FPR^{-1}(\alpha)]). \]
如果我们粗粗地观察地话, 可以发现, \(\text{OPAUC}(\beta)\) 相比于 AUC 来说更加关注困难样本.
所以, 有些时候我们可能会希望去最大化 OPAUC 而不是 AUC, 而 OPAUC 可以通过下式估计:

\[\widehat{\text{OPAUC}}(\beta) = \frac{1}{|\mathcal{C}|} \sum_{c \in \mathcal{C}} \frac{1}{n_+ n_-} \sum_{i \in \mathcal{I}_c^+} \sum_{j \in \mathcal{S}_{\mathcal{I}_c^-}^{\downarrow} [1, n_- \cdot \beta]} \mathbb{I}(r_{ci} > r_{cj}). \]
不过, OPAUC 由于其 non-smooth 的特性, 没有办法直接优化, 所以一般来说我们会用 \(L(c, i, j) = \ell(r_{ci} - r_{cj})\) 去替代 \(\mathbb{I}\), 得到:

\[\frac{1}{|\mathcal{C}|} \sum_{c \in \mathcal{C}} \frac{1}{n_+ n_-} \sum_{i \in \mathcal{I}_c^+} \sum_{j \in \mathcal{S}_{\mathcal{I}_c^-}^{\downarrow} [1, n_- \cdot \beta]} L(c, i, j). \]
通常, \(\ell\) 被要求是可微的单调递减的函数, 比如 logistic loss \(\ell (t) = \log (1 + \exp(-t))\).
作者证明了:
1. 当 \(P_{ns}\) 为 DNS:
  
  \[P_{ns}^{DNS}(j | c) = \left \{ \begin{array}{ll} \frac{1}{M} & j \in \mathcal{S}_{\mathcal{I}_c^-}^{\downarrow} [1, M] \\ 0 & j \in others, \end{array} \right . \]
  且 \(M = n_- \cdot \beta\) 时, \(\text{OPAUC}(\beta)\) 和 BPR 是等价的.
2. 当 \(P_{ns}\) 为:
  
  \[P_{ns}^{softmax} (j | c) = \frac{\exp(r_{cj}/ \tau)}{\sum_{k \in \mathcal{I}_c^-} \exp(r_{ck} / \tau)}, \]
  且满足
  
  \[\tau = \sqrt{\frac{\text{Var}_j (L(c, i, j))}{-2\log \beta}}, \]
  其中
  
  \[\text{Var}_j (L(c, i, j)) = \mathbb{E}_{j \in \frac{1}{n_-}} [(L(c, i, j) - \mathbb{E}_{j \sim \frac{1}{n_-}}[L(c, i, j)^2])] \]
  的时候, \(\text{OPAUC} (\beta)\) 和 BPR 是相近的.
换言之, 之前广受欢迎的 BPR 损失是一个 \(\text{OPAUC}\) 取特殊的 \(\beta\) 的情形, 倘若我们能够挑选更合适的 \(\beta\), 或许能够有更好的结果.

OPAUC 与 Top-K 指标

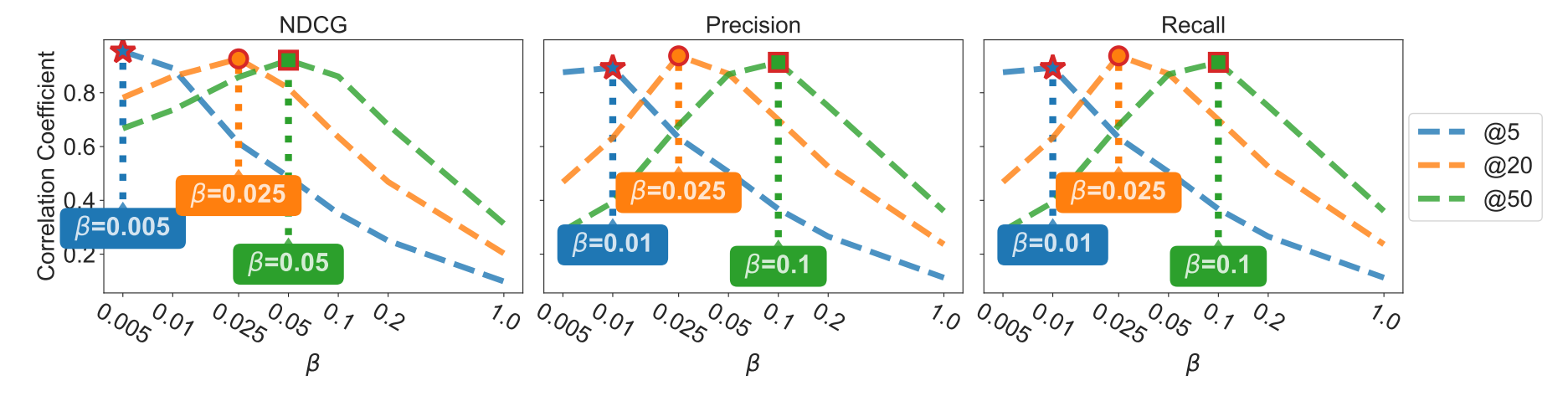
作者证明, 在 \(N_+ > K, N_- > K\) 的情况下, 有以下性质成立 (分别探讨 OPAUC 的最佳和最差结果可证):
对于 \(\beta = K / N_-\) 这一特殊情况, 我们有: 倘若我们希望模型能够更加关注 K 更小的情况下的指标, 那么在训练过程中需要挑选更为复杂难度更大的负样本, 反之亦然的结论. 对于 AUC 自然没有这样的结论.
作者进行了模拟实验进行验证: