Neural Ordinary Differential Equations

目录

• 概
• 符号说明
• 基本框架
• 连续的反向传播
• 代码

Chen R. T. Q., Rubanova Y., Bettencourt J. and Duvenaud D. Neural ordinary differential equations. In Advances in Neural Information Processing Systems (NIPS), 2018.

概

本文提出了一种新的网络架构, 从 ODE 出发, 将神经网络的中间状态视作 ODE 中的某个状态, 而我们所需要做的只是拟合整个过程的 '动力' 部分, 即梯度.

符号说明

• ODE:

  $$\tag{1} \frac{d \bm{h}(t)}{dt} = f(\bm{h}(t), t),$$

  给定初始值 $\bm{h}(0)$, 也可以写成如下的积分形式:

  $$\tag{2} \bm{h}(t) = \bm{h}(0) + \int_{0}^t f(\bm{h}(\tau), \tau) \: d \tau.$$

• 对于 $f(\bm{x}): \mathbb{R}^{d} \rightarrow \mathbb{R}^{d'}$, 定义

  $$\nabla_{\bm{x}} f = \left [ \begin{array}{cccc} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_2}{\partial x_1} & \cdots & \frac{\partial f_{d'}}{\partial x_1} \\ \frac{\partial f_1}{\partial x_2} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_{d'}}{\partial x_2} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_{1}}{\partial x_d} & \frac{\partial f_{2}}{\partial x_d} & \cdots & \frac{\partial f_{d'}}{\partial x_d} \end{array} \right ] \in \mathbb{R}^{d \times d'}.$$

基本框架

• 设想我们给定一输入 $\bm{z}(t_0)$, 我们希望拟合'动力' $f(\bm{z}(t), t; \theta)$ 来推动其状态

  $$\tag{3} \bm{z}(t_0) \rightarrow \bm{z}(T; \theta) = \bm{z}(t_0) + \int_{t_0}^T f(\bm{z}(\tau), \tau; \theta) d\tau.$$

• 然后我们利用最终状态 $\bm{z}(T)$ 来进行一些下游任务. 我们训练 $\theta$, 我们可以利用损失函数:

  $$\tag{4} \mathcal{L}(\bm{z}(T; \theta))$$

  进行训练.

• 通常 $\bm{z}(t_0) \rightarrow \bm{z}(T)$ 不是傻乎乎积分得到的, 而是通过一些数值近似方法, 比如: Euler 方法:

  $$\tag{5} \bm{h}(t + s) = \bm{h}(t) + s f(\bm{h}(t), t),$$

  其中 $s$ 是每一步迭代的步长.

• 非常有意思的是, 当我们去 $s=1$ 的时候:

  $$\tag{6} \bm{h}(t) = \bm{h}(t) + f(\bm{h}(t), t),$$

  这实际上就是鼎鼎大名的残差连接. 当然对于 ResNet 而言, 它的'动力模块' $f(\bm{h}(t); \theta_t)$ 对于每一个 block 都是不同的. 而 NODE 的思想是我们只拟合一个这样的'动力模块'.

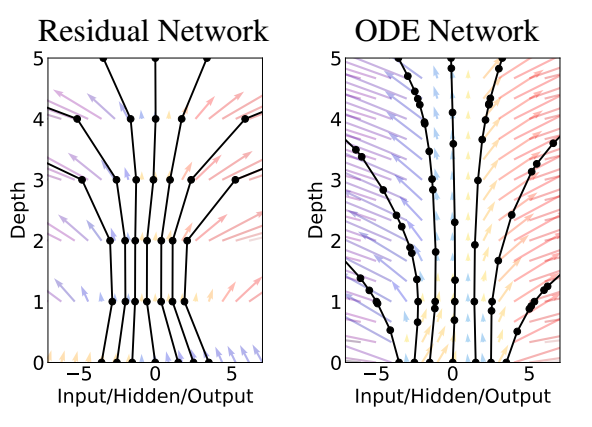
• 那么 NODE 的优势体现在哪儿呢 ? 就是对于 (3) 的近似上, 我们不单单可以采用简单的 Euler 方法 ($s$=1), 步长可以更加精细, 甚至可以学习, 此外也可以用一下更复杂的数值近似方法, 比如 Runge-Kutta.

连续的反向传播

• 为了能够训练 $\theta$, 前提是我们能够计算出梯度

  $$\tag{7} \nabla_{\theta} \mathcal{L}.$$

• 为了便于推导, 我们假想 $\theta, t$ 也随着整个过程变化, 只是

  $$\tag{8} \nabla_{t} \theta (t) = 0, \: \frac{dt(t)}{dt} = 1.$$

• 此时我们可以定义

  $$\tag{9} \bm{a}(t) := \nabla_{\bm{z}(t)} \mathcal{L}, \\ \bm{a}_{\theta}(t) := \nabla_{\bm{\theta}(t)} \mathcal{L}, \\ a_t(t) := \frac{d \mathcal{L}}{d t(t)}.$$

• 再定义增广的向量:

  $$\tag{10} \bm{z}_{aug} := \left [ \begin{array}{c} \bm{z}(t) \\ \theta(t) \\ t(t) \end{array} \right ], \quad f_{aug}(\bm{z}_{aug}) = \left [ \begin{array}{c} f(\bm{z}_{aug}) \\ \bm{0} \\ 1 \end{array} \right ], \quad \bm{a}_{aug} = \left [ \begin{array}{c} \bm{a} \\ \bm{a}_{\theta} \\ a_t \end{array} \right ].$$

• 于是我们可以将 (3) 改写为

  $$\tag{11} \bm{z}_{aug} (t) = \bm{z}_{aug}(t_0) + \int_{t_0}^t f_{aug}(\bm{z}_{aug}(\tau)) d\tau.$$

• 另一种有助于求梯度的形式:

  $$\tag{12} \bm{z}_{aug} (t + \epsilon) = \bm{z}_{aug}(t) + \int_{t}^{t+\epsilon} f_{aug}(\bm{z}_{aug}(\tau)) d\tau.$$

• 可知 (链式法则):

  $$\tag{13} \bm{a}_{aug}(t) = \nabla_{\bm{z}_{aug}(t)} \mathcal{L} = \nabla_{\bm{z}_{aug}(t)} \bm{z}_{aug}(t+\epsilon) \: \nabla_{\bm{z}_{aug}(t+\epsilon)}\mathcal{L} = \nabla_{\bm{z}_{aug}(t)} \bm{z}_{aug}(t+\epsilon)\: \bm{a}_{aug}(t+\epsilon)$$

• 此外, 注意到 (12) 的一阶泰勒近似为:

  $$\tag{14} \begin{array}{ll} &\bm{z}_{aug}(t + \epsilon) = \bm{z}_{aug}(t) + f_{aug}(\bm{z}_{aug}(t)) \epsilon + \mathcal{O}(\epsilon^2) \\ \Rightarrow& \nabla_{\bm{z}_{aug}(t)} \bm{z}_{aug}(t+\epsilon) = I + \epsilon \nabla_{\bm{z}_{aug}(t)} f_{aug} + \mathcal{O}(\epsilon^2), \end{array}$$

  其中

  $$\tag{15} \nabla_{\bm{z}_{aug}(t)} f_{aug}(\bm{z}_{aug}(t)) = \left [ \begin{array}{ccc} \nabla_{\bm{z}}f & \bm{0} & \bm{0} \\ \nabla_{\theta} f & \bm{0} & \bm{0} \\ \frac{d f}{ dt} & \bm{0} & 0 \\ \end{array} \right ].$$

  注: 这里和下面的 $\nabla_{\theta} f(\bm{z}, \theta)$ 都是指关于 $\theta$ 变元求梯度 (此时不能再通过 $\nabla_{\theta} \bm{z}$ 再求导下去), 否则加上就乱套了, 也就是说, 我们在这里简单地认为 $\bm{z}$ 和 $\theta$ 无关.

• 故

  $$\tag{16} \begin{array}{ll} \frac{d \bm{a}_{aug}(t)}{dt} &=\lim_{\epsilon \rightarrow 0} \frac{\bm{a}_{aug}(t + \epsilon) - \bm{a}_{aug}(t)}{\epsilon} \\ &=\lim_{\epsilon \rightarrow 0} \frac{\bm{a}_{aug}(t + \epsilon) - \nabla_{\bm{z}_{aug}(t)} \bm{z}_{aug}(t+\epsilon)\: \bm{a}_{aug}(t+\epsilon)}{\epsilon} \\ &=\lim_{\epsilon \rightarrow 0} \frac{\bm{a}_{aug}(t + \epsilon) - (I + \epsilon \nabla_{\bm{z}_{aug}(t)} f_{aug} + \mathcal{O}(\epsilon^2)) \bm{a}_{aug}(t+\epsilon)}{\epsilon} \: \leftarrow (14) \\ &=\lim_{\epsilon \rightarrow 0} -\frac{\Big\{\epsilon \nabla_{\bm{z}_{aug}(t)} f_{aug} + \mathcal{O}(\epsilon^2)\Big \} \bm{a}_{aug}(t + \epsilon) }{\epsilon} \\ &=\lim_{\epsilon \rightarrow 0} -\Big\{\nabla_{\bm{z}_{aug}(t)} f_{aug} + \mathcal{O}(\epsilon)\Big \} \bm{a}_{aug}(t + \epsilon) \\ &=-\nabla_{\bm{z}_{aug}(t)} f_{aug}(\bm{z}_{aug})\bm{a}_{aug}(t) . \end{array}$$

• 具体地 (根据 (15)):

  $$\tag{17} \frac{d\bm{a}(t)}{dt} = - [\nabla_{\bm{z}} f] \: \bm{a}, \\ \frac{d\bm{a}_{\theta}(t)}{dt} = - [\nabla_{\bm{\theta}} f] \: \bm{a}, \\ \frac{da_{t}(t)}{dt} = - \frac{d f}{dt} \: \bm{a}. \\ $$

• 于是乎:

  $$\tag{18} \nabla_{\bm{z}(t)} \mathcal{L} = \bm{a}(t) = \bm{a}(T) - \int_{T}^{t} [\nabla_{\bm{z}} f(\bm{z}(\tau), \tau; \theta)] \bm{a}(\tau) d\tau, \\ \nabla_{\theta(t)} \mathcal{L} = \bm{a}_{\theta}(t) = \bm{a}_{\theta}(T) - \int_{T}^{t} [\nabla_{\bm{\theta}} f(\bm{z}(\tau), \tau; \theta)] \bm{a}(\tau) d\tau, \\ \nabla_{t(t)} \mathcal{L} = a_{t}(t) = a_{t}(T) - \int_{T}^{t} [\nabla_{t} f(\bm{z}(\tau), \tau; \theta)] \bm{a}(\tau) d\tau.$$

  其中

  $$\tag{19} \bm{a}(T) = \nabla_{\bm{z}(T)} \mathcal{L}, \\ a_t(T) = \nabla_{\bm{z}(T)} \mathcal{L} \: \nabla_{T}\bm{z}(T) = [\nabla_{\bm{z}(T)} \mathcal{L}] \: f(\bm{z}(T), T; \theta).$$

  至于 $\bm{a}_{\theta}(T)$ 作者说可以设它为 $\bm{0}$, 个人感觉是因为:

  $$\tag{20} \begin{array}{ll} \bm{a}_{\theta}(T) &=\nabla_{\theta_T} \mathcal{L} &=\nabla_{\bm{z}(T)} \mathcal{L} \: \nabla_{\theta_T} \bm{z}(T) &=\nabla_{\bm{z}(T)} \mathcal{L} \Big\{\nabla_{\theta_T} \int_{t_0}^T f(\bm{z}(\tau), \tau; \theta(\tau)) d\tau \Big\}, \end{array}$$

  由于在积分中 $\theta_T$ 只有一瞬, 故可以认为 $\bm{a}_{\theta}(T) = \bm{0}$. 不晓得这么理解正确与否.

• 让我们再通过离散化来仔细分析一下, 假设定性 $[t_0, T]$ 为 $[0, K]$, 并用一般的 Euler 方法进行前向的扩散 (且步长为 $1$), 则

  $$\bm{z}(t + 1) = \bm{z}(t) + \bm{f}(\bm{z}(t), t; \theta), \: t=0,1, \cdots, K-1.$$

• 倘若我们对 (18) 也采用 Euler 的方式近似:

  $$\begin{array}{ll} \bm{a}_{\theta}(t) &=\bm{a}_{\theta}(t+1) + \nabla_{\theta} f(\bm{z}(t + 1), t + 1; \theta) \: \nabla_{\bm{z}(t+1)} \mathcal{L}. \\ &\approx \bm{a}_{\theta}(t+1) + \nabla_{\theta} f(\bm{z}(t), t; \theta) \: \nabla_{\bm{z}(t+1)} \mathcal{L}. \\ \end{array}$$

  故

  $$\bm{a}_{\theta}(0) \approx \sum_{t=0}^{T-1} \nabla_{\theta} \bm{f}(z(t), t; \theta) \: \nabla_{\bm{z}(t+1)} \mathcal{L}.$$

  这完全和我们直接利用反向传播公式得到的结果是一致的.

• 当然, 也可以用一般的 ODE Solver 来更加复杂地近似求解梯度, 正如作者给出的算法 (符号和这里定义的略有不同):
  

注: 我看了一篇契合 NODE 的应用于推荐系统的文章, 发现他仅仅是在前向的过程中用到了 ODE Solver, 后向就是用的普通的传播, 如果仅仅这样效果就很好了的话, 那这个潜力还是相当大的. 因为很重要的一点是时间 $t$ 实际上都是可以训练的, 这意味着我们的模块间的远近都可以自动学习.

注: 在各个场景下的应用也是非常精彩的.

代码

[torchdiffeq]