Diffusion Probability Model
本文梳理一下 VAE -> Flow -> Diffusion 的过程 [9]. 需要声明的是, 个人是没有进行过这方面的实践的, 相关的理论只是也比较匮乏, 这里只是一个对这些从事贝叶斯网络研究满怀敬意的人的纸上谈兵了. 扩散模型没有被时间洪流所掩埋, 真是让人感动的事情.
符号说明
- \(\bm{x} \in \mathbb{R}^d\), 数据向量, 服从某个分布;
- 我们通常以 \(p(\bm{x}), q(\bm{x})\) 来表示某种分布;
- \(|A|, \text{det}(A)\), 矩阵 \(A\) 的行列式;
- \(\nabla f, \nabla \cdot f\), 梯度算子;
- \(\mathbf{KL}(p\|q)\), KL 散度;
前言
-
无论是 VAE, 还是 Flow, 亦或是现在流行的 Diffusion 模型, 都是在建模生成模型 \(p(\bm{x})\):
- 有了概率模型 \(p(\bm{x})\), 我们就可以从中采样 (虽然, 如何采样本身也是一个问题), 这就是很好玩的图像生成的来源;
- 倘若我们还能够建模 \(p(\bm{x}, \bm{y})\) (这里 \(\bm{y}\) 是某个, 比如标签), 我们还可以做条件采样 (根据 \(p(\bm{x}|\bm{y})\)), 或者分类任务 \(\hat{\bm{y}} := \arg\max_{\bm{y}} \: p(\bm{y}|\bm{x})\).
-
遗憾的是, 我们从接下来的一些章节中可以发现, 这是一个相当困难的问题.
VAE
-
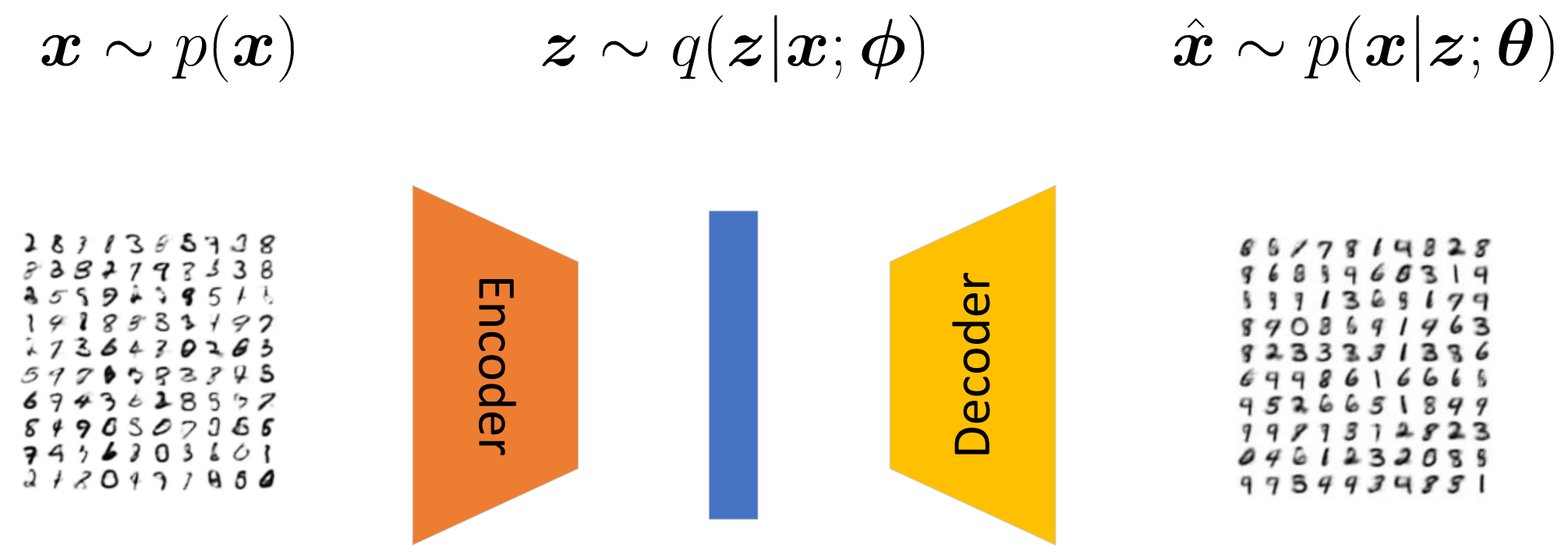
VAE [1] (即变分自编码) 的思路是, 首先将样本 \(\bm{x}\) 映射到一个低维的空间中, 隐特征 \(\bm{z}\) 服从一个分布, 我们需要从中采样 (如果不采样就变成自编码了), 然后再经过 decoder 将隐变量 \(\bm{z}\) 映射回到源空间.
-
我们的目标是构建 \(p(\bm{x}; \theta)\) 去拟合真实的分布 \(p(\bm{x})\), 但是仔细想, 我们很难直接用现存的简单的分布来建模, 所以我们通常转而利用一个联合分布 \(p(\bm{x}, \bm{z}; \theta)\) 来建模, 同时希望
\[p(\bm{x}; \theta) = \int_{\bm{z}} d\bm{z} \: p(\bm{x, \bm{z}}; \theta) \approx p(\bm{x}). \] -
具体的, 作者希望构建一个 decoder 来建模 \(p(\bm{x}|\bm{z}; \theta)\):
- 比如, 我们将其建模为 \(\hat{\bm{x}}|\bm{z} \sim \mathcal{N}(\bm{x}; \bm{\mu}_{\theta}(\bm{z}), \bm{\sigma}_{\theta}(\bm{z}) I)\), 这里 \(\bm{\mu}_{\theta}, \bm{\sigma}_{\theta}\) 分别建模了均值和方差;
-
然后我们通过极大对数似然优化
\[\max_{\theta} \: \mathbb{E}_{p(\bm{x})} \Big[ \log p(\bm{x}; \theta) \Big] \approx \sum_{i=1}^N \log p(\bm{x}_i; \theta) . \] -
但是, 还是那个问题, 我们通常是写不出 \(p(\bm{x}; \theta)\) 的显式形式的, 所以 VAE 的思路是采用 ELBO.
-
注意到
\[\tag{1} \begin{array}{ll} \log p(\bm{x}; \theta) &=\log \int_{\bm{z}} d\bm{z} \: p(\bm{x, \bm{z}}; \theta) \\ &=\log \int_{\bm{z}} d\bm{z} \frac{p(\bm{x, \bm{z}}; \theta) \cdot q(\bm{z}|\bm{x}; \phi)}{q(\bm{z}|\bm{x}; \phi)} \\ &=\log \mathbb{E}_{q_{\phi}} [\frac{p(\bm{x, \bm{z}}; \theta)}{q(\bm{z}|\bm{x}; \phi)}] \\ &\ge \mathbb{E}_{q_{\phi}} \Bigg \{ \log \Big[ \frac{p(\bm{x, \bm{z}}; \theta)}{q(\bm{z}|\bm{x}; \phi)} \Big] \Bigg \} \quad \leftarrow \text{Jensen's Inequality} \\ &= \mathbb{E}_{q_{\phi}} \Bigg \{ \log \Big[ \frac{p(\bm{x}| \bm{z}; \theta) p(\bm{z})}{q(\bm{z}|\bm{x}; \phi)} \Big] \Bigg \} \\ &= \mathbb{E}_{q_{\phi}} \Bigg \{ \Big[\log \frac{p(\bm{z})}{q(\bm{z}|\bm{x}; \phi)} + \log p(\bm{x}| \bm{z}; \theta) \Big] \Bigg \} \\ &= \underbrace{\mathbb{E}_{q_{\phi}}[\log p(\bm{x}|\bm{z}; \theta)]}_{\text{ reconstruction term }} - \underbrace{\mathbf{KL}(q_{\phi}(\bm{z}|\bm{x})\| p(\bm{z}))}_{ \text{prior matching term} }. \end{array} \]最后两项分别为重构项和先验匹配项. 最大化 ELBO 实际上是最大化的下界.
-
实际上,
\[\log p(\bm{x}; \theta) - [\mathbb{E}_{q_{\phi}}[\log p(\bm{x}|\bm{z}; \theta)] - \mathbf{KL}(q_{\phi}(\bm{z}|\bm{x})\| p(\bm{z}))] = \mathbf{KL}(q_{\phi}(\bm{z|x})\|p(\bm{z|x})), \]即这个下界的优劣取决于我们的 encoder 对于后验分布 \(p(\bm{z|x})\) 拟合得好不好.
Flow
-
Flow [2, 4] 其实已经非常接近 Diffusion 的思想了, Flow 的初衷是为了解决 VAE 的假设分布通常过于简单 (比如高斯) 的问题而诞生的.
-
它的思路是:
-
首先和一般的 VAE 一样构建拟合的后验分布 \(q(\bm{z}_0|\bm{x}; \phi)\), 对于 VAE 它就会假设 \(q(\bm{z}_0|\bm{x}; \phi)\) 为 \(\mathcal{N}(\bm{z}; \mu_{\phi}(\bm{x}), \Sigma_{\phi}(\bm{x}))\), 显然这就定死了隐变量的形式只能是这种简单的容易采样的分布;
-
Flow 是在此基础上, 通过构造一些特殊的可逆变换 \(f_t: \bm{z} \rightarrow \bm{z}, \: t=1,2\ldots, T\), 于是得到
\[\bm{z}_T = f_T(\bm{z}_{T-1}) = f_T \circ f_{T-1} \circ \cdots \circ \bm{z}_0. \]这种特殊的变换, 通常要求其雅可比行列式 \(|\text{det}(\nabla_{\bm{z}_{t-1}}f_t)|\) 是容易获得的.
-
在 \(\bm{z}_T\) 的基础上, 构建 decoder.
-
在此基础上, 套用 (1) 可以得到
\[\tag{2} \begin{array}{ll} \log p(\bm{x}; \theta) &\ge \mathbb{E}_{q_{\phi}(\bm{z}_T|\bm{x})} \Bigg \{ \log \Big[ \frac{p(\bm{x, \bm{z}_T}; \theta)}{q(\bm{z}_T|\bm{x}; \phi)} \Big] \Bigg \} \\ &= \mathbb{E}_{q_{\phi}(\bm{z}_0|\bm{x})} \Bigg \{ \log p(\bm{x, \bm{z}_T}; \theta) - \log q(\bm{z}_T|\bm{x}; \phi) \Bigg \} \: \leftarrow \text{ 可逆 } \\ &= \mathbb{E}_{q_{\phi}(\bm{z}_0|\bm{x})} \log p(\bm{x, \bm{z}_T}; \theta) - \mathbb{E}_{q_{\phi}(\bm{z}_0|\bm{x})} \log q(\bm{z}_T|\bm{x}; \phi) \: \leftarrow \text{ 可逆 } \\ &= \mathbb{E}_{q_{\phi}(\bm{z}_0|\bm{x})} \log p(\bm{x, \bm{z}_T}; \theta) - \Big \{ \mathbb{E}_{q_{\phi}(\bm{z}_0|\bm{x})} \log q(\bm{z}_T|\bm{x}; \phi) \Big \}\\ &= \mathbb{E}_{q_{\phi}(\bm{z}_0|\bm{x})} \log p(\bm{x, \bm{z}_T}; \theta) - \mathbb{E}_{q_{\phi}(\bm{z}_0|\bm{x})} \Big \{ \log q(\bm{z}_0|\bm{x}; \phi) - \sum_{t=1}^T \log |\text{det}(\nabla_{\bm{z}_{t-1}}f_t)| \Big \}. \end{array} \]其中最后一步是根据积分变换的性质得到的: 倘若 \(\bm{Z}' = f(\bm{Z})\), 且 \(f\) 可逆, 若 \(\bm{Z}\) 的密度函数为 \(p(\bm{Z})\), 则
\[\tag{3} p(\bm{Z}') = p(\bm{Z}) |\text{det}(\nabla_z f)|^{-1}. \]
-
注: 这里 \(|\cdot|\) 表示绝对值, 在下文中, 我们会用 \(|A| := \text{det}(A)\).
VAE -> Diffusion
-
Diffusion 的理论框架 [3] 其实和 FLow [2] 是同一年的 ICML 上被提出来的, 只能说英雄所见略同啊.
-
VAE 有一个很强的愿望 (我不清楚原作者是否在意这个部分), 就是希望提取出一个隐变量 \(\bm{z}\), 且隐变量 \(\bm{z}\) 和样本 \(\bm{x}\) 是强相关的. 但是实际上, 只要我们找到一个联合分布 \(p(\bm{x,z}; \theta)\) 满足
\[\int_z d \bm{z} \: p(\bm{x}, \bm{z}; \theta) \approx p(\bm{x}) \]成立, 那么这个就可以做我们的分布. 只是通常这样做, 我们很难找到一个简单的容易拟合也容易采样的分布.
-
换言之, 理论上隐变量 \(\bm{z}\) 只是 VAE 的一个副产物 (基于前人美好的设想, 认为这样有助于生成模型的学习, 毕竟隐变量的维度比较低, 比较容易避免维度灾难的问题).
-
事实上, 给定数据分布 \(p(\bm{x})\) 和一个先验分布 \(p(\bm{z})\), 存在无穷多的后验分布 \(q(\bm{z}|\bm{x}; \phi)\) 使得所对应的联合分布 \(p(\bm{x}, \bm{z}) = p(\bm{x})q(\bm{z}|\bm{x}; \phi)\) 满足边际分布 \(p(\bm{z})\). 同理, 对于 \(p(\bm{x}|\bm{z}; \theta)\) 也有同样的观点. 这说明, VAE 其实拟合的是一个不定的问题, \(p_{\theta}, q_{\phi}\) 并没有一个确切的方向去学习. 这或许会导致训练起来不是那么高效 (个人看法).
-
抛开对隐变量的执念, 我们只需要固定 \(q_{\phi}\) 或者 \(p_{\theta}\) 然后专心拟合另外一个就可以了. 于是, DPM 实际上就是构造了 \(q\), 它保证
\[p(\bm{x}_0) = \int d\bm{z}_{1:T} \: q(\bm{x}_0, \bm{z}_{1:T}) \]的严格成立. 如此以来, 我们只需要转型负责 \(p_{\theta}\) 的构造和拟合即可. 当然为了上式构造方便, DPM 采用 \(\bm{z}_t = \bm{x}_t\), 维度不变的设计. 当然, 我们失去了隐变量, 这一副产品.
-
这里需要特别说明的是, 虽然没了隐变量, 对 DPM 的操控也是可行的, 况且, 在普通的 VAE 的隐变量上直接操控通常也是困难的 (我们很难说清楚哪个维度到底对应了那些特征).
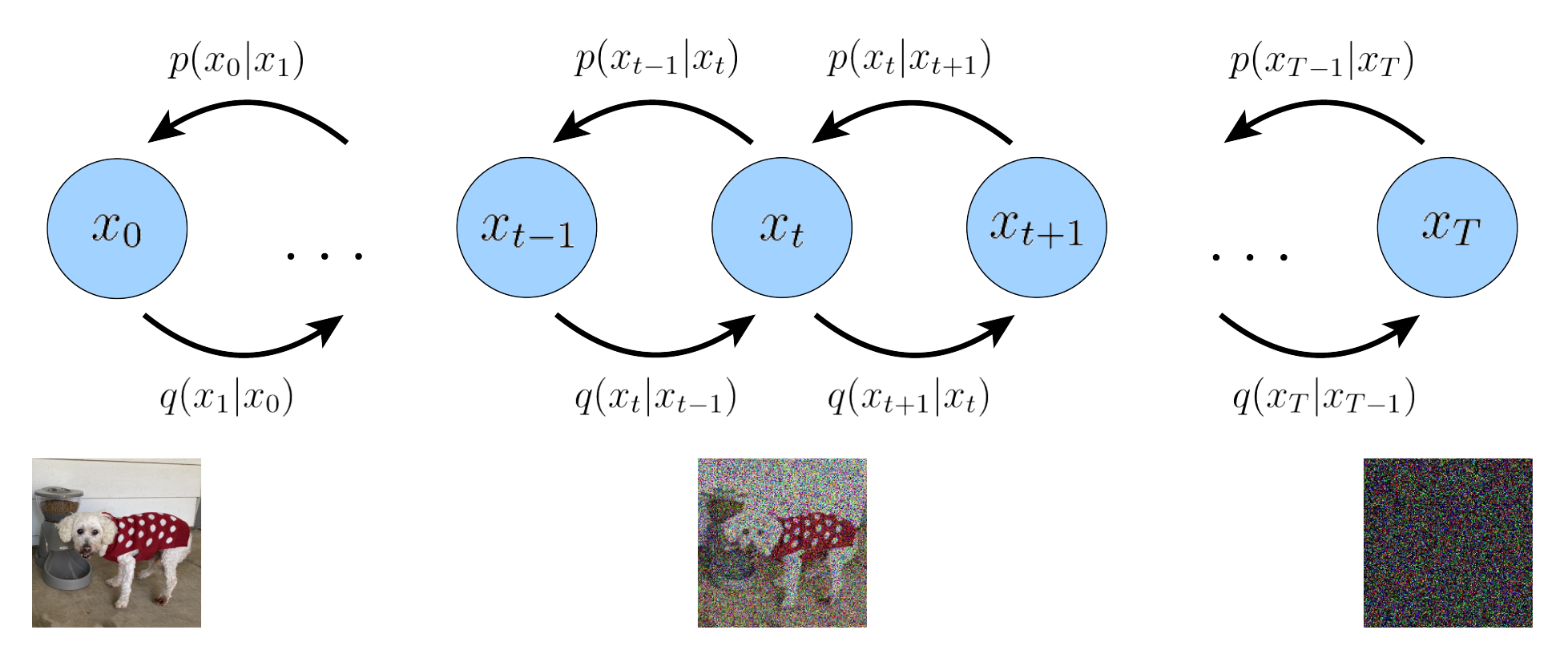
前向扩散过程
-
首先是一个前向扩散的过程, 我们在原始真实分布 \(p(\bm{x}_{0})\) 的基础上, 构建一系列的中间过程
\[q(\bm{x}_{t}| \bm{x}_{t-1}), \quad t=1,2, \cdots T, \]具体的, 比如 (一会儿我们会看到这么设计的用处)
\[q(\bm{x}_{t}| \bm{x}_{t-1}) \sim \mathcal{N}(\bm{x}_{t}; \sqrt{1 - \beta_t}\bm{x}_{t-1}, \beta_t \bm{I}). \]这里 \(\beta_t\) 是扩散率. 需要特别注意的是, 这里的一步步逼近是确定的, 并非是美好的期望, 所以这里我们这个扩散过程并没有拟合的问题. 实际上, 我们可以显式地求解出 \(q(\bm{x}_t|\bm{x}_0)\) 来.
-
注意到
\[\tag{4} \begin{array}{ll} \bm{x}_t &= \sqrt{1 - \beta_t} \bm{x}_{t-1} + \sqrt{\beta_t} \bm{\epsilon}, \: \leftarrow \bm{\epsilon} \sim \mathcal{N}(\bm{0}, I) \\ &= \sqrt{1 - \beta_t} (\sqrt{1 - \beta_{t-1}} \bm{x}_{t-2} + \sqrt{\beta_{t-1}} \bm{\epsilon}') + \sqrt{\beta_t} \bm{\epsilon} \\ &= \sqrt{1 - \beta_t}\sqrt{1 - \beta_{t-1}} \bm{x}_{t-2} + \sqrt{1 - \beta_t}\sqrt{\beta_{t-1}} \bm{\epsilon}' + \sqrt{\beta_t} \bm{\epsilon} \\ &= \sqrt{1 - \beta_t}\sqrt{1 - \beta_{t-1}} \bm{x}_{t-2} + \sqrt{1 - (1 - \beta_t)(1 - \beta_{t-1})} \bm{\epsilon} \: \leftarrow \text{Q1?} \\ &= \cdots \\ &= (\prod_{s=1}^t \sqrt{1 - \beta_s}) \bm{x}_0 + \sqrt{1 - \prod_{s=1}^t (1 - \beta_s)} \bm{\epsilon}, \end{array} \]Q1 的部分是因为 \(\bm{\epsilon}', \bm{\epsilon}\) 独立同分布, 二者的和依旧是正态分布, 于是:
\[\tag{5} \begin{array}{ll} &\text{cov}(\sqrt{1 - \beta_t}\sqrt{\beta_{t-1}} \bm{\epsilon}' + \sqrt{\beta} \bm{\epsilon}, \sqrt{1 - \beta_t}\sqrt{\beta_{t-1}} \bm{\epsilon}' + \sqrt{\beta} \bm{\epsilon} ) \\ =&\text{cov}(\sqrt{1 - \beta_t}\sqrt{\beta_{t-1}} \bm{\epsilon}' , \sqrt{1 - \beta_t}\sqrt{\beta_{t-1}} \bm{\epsilon}') + \text{cov}(\sqrt{\beta}\bm{\epsilon}, \sqrt{\beta}\bm{\epsilon}) \\ =& (1 - \beta_t)(\beta_{t-1}) I + \beta_t I \\ =& (1 - (1 - \beta_t)(1 - \beta_{t-1})) I. \end{array} \]最后的最后可以通过归纳法来得到, 这里不多赘述了.
-
由此可知
\[\tag{6} q(\bm{x}_t|\bm{x}_0) \Leftrightarrow \mathcal{N}(\bm{x}_t; \Big [\prod_{s=1}^t \sqrt{1 - \beta_s}\Big] \bm{x}_0, \Big [1 - \prod_{s=1}^t (1 - \beta_s)\Big] \: I). \]我们可以令 \(\bar{\alpha}_t := \prod_{s=1}^t \alpha_s, \: \alpha_s := 1 - \beta_s\), 则
\[\tag{7} q(\bm{x}_t|\bm{x}_0) \Leftrightarrow \mathcal{N}(\bm{x}_t; \sqrt{\bar{\alpha}_t} \bm{x}_0, (1 - \bar{\alpha}_t) I). \]此外还有性质
\[\tag{8} (1 - \bar{\alpha}_{t-1})(1 - \beta_t) + \beta_t = (1 - \bar{\alpha}_{t-1})\alpha_t + \beta_t = \alpha_t - \bar{\alpha}_t + \beta_t = 1 - \bar{\alpha}_t. \] -
此外, 我们还可以求出 \(q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0)\):
\[\tag{9} \begin{array}{ll} q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0) &= \frac{q(\bm{x}_t|\bm{x}_{t-1}, \bm{x}_0)q(\bm{x}_{t-1}|\bm{x}_0)}{q(\bm{x}_t|\bm{x}_0)} \\ &= \frac{q(\bm{x}_t|\bm{x}_{t-1})q(\bm{x}_{t-1}|\bm{x}_0)}{q(\bm{x}_t|\bm{x}_0)} \: \leftarrow \text{ 马氏性 }\\ &\propto q(\bm{x}_t|\bm{x}_{t-1})q(\bm{x}_{t-1}|\bm{x}_0) \leftarrow \text{ 关注核即可} \\ &\propto \exp\Bigg\{-\frac{1}{2 (1 - \bar{\alpha}_{t-1})\beta_t} \bigg[(1 - \bar{\alpha}_{t-1}) \|\bm{x}_t - \sqrt{1 - \beta_t} \bm{x}_{t-1}\|^2 + \beta_t \|\bm{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}}\bm{x}_0\|^2 \bigg]\Bigg\} \\ &\propto \exp\Bigg\{-\frac{1}{2 (1 - \bar{\alpha}_{t-1})\beta_t} \bigg[(1 - \bar{\alpha}_t)\|\bm{x}_{t-1}\|^2 - 2(1 - \bar{\alpha}_{t-1}) \sqrt{\alpha_t} \bm{x}_t^T\bm{x}_{t-1} - 2 \sqrt{\bar{\alpha}_{t-1}} \beta_t \bm{x}_0^T \bm{x}_{t-1} \bigg]\Bigg\}. \\ \end{array} \]于是, 根据核可知, 分布为高斯分布, 且
\[\tag{10} q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0) \Leftrightarrow \mathcal{N}(\bm{x}_{t-1}; \underbrace{\frac{\sqrt{\bar{\alpha}_{t-1}}(1 - \alpha_t) \bm{x}_0 + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})\bm{x}_t}{1 - \bar{\alpha}_t}}_{=: \bm{\mu}_t (\bm{x}_t, \bm{x}_0)}, \underbrace{\frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}}_{=: \sigma_t^2} I). \]
反向采样过程
-
反向采样过程即是上述过程的一个逆过程, 从 \(p(\bm{x}_T)\) 出发, 从联合分布
\[\tag{11} p(\bm{x}_{0:T}; \theta) = p(\bm{x}_T) \prod_{t=1}^T p(\bm{x}_{t-1}| \bm{x}_{t}; \theta), \]中即可采样得到一组序列
\[\bm{x}_T, \bm{x}_{T-1} \cdots \bm{x}_0, \]我们期望通过 \(\theta\) (故反向采样过程是需要训练的) 使得最后的 \(\bm{x}_0\) 是服从真实分布 \(p(\bm{x}_0)\) 的.
-
自然地, 和 VAE, Flow 的方式一样, 我们希望通过对数似然来优化
\[\tag{12} \begin{array}{ll} \log p(\bm{x}_0) &= \log \int_{\bm{x}_{1:T}} d \bm{x}_{1:T} \: p(\bm{x}_{0:T}; \theta) \\ &= \log \int_{\bm{x}_{1:T}} d \bm{x}_{1:T} \: \frac{p(\bm{x}_{0:T}; \theta) \cdot q(\bm{x}_{1:T}|\bm{x}_0)}{q(\bm{x}_{1:T}|\bm{x}_0)} \\ &= \log \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Big [\frac{p(\bm{x}_{0:T}; \theta) }{q(\bm{x}_{1:T}|\bm{x}_0)} \Big ] \\ &\ge \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \log \Big [\frac{p(\bm{x}_{0:T}; \theta)}{q(\bm{x}_{1:T}|\bm{x}_0)} \Big ] \leftarrow \text{ Jensen's Inequality } \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \log \Big [\frac{p(\bm{x}_T) \prod_{t=1}^T p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{\prod_{t=1}^T q(\bm{x}_{t}|\bm{x}_{t-1})} \Big ] \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Bigg\{ \log \frac{p(\bm{x}_T)p(\bm{x}_0|\bm{x}_1; \theta)}{q(\bm{x}_T|\bm{x}_{T-1})} + \sum_{t=1}^{T-1} \log \frac{p(\bm{x}_{t}| \bm{x}_{t+1}; \theta)}{q(\bm{x}_{t}|\bm{x}_{t-1})} \Bigg \} \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)}[\log p(\bm{x}_0|\bm{x}_1; \theta)] + \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} [\log \frac{p(\bm{x}_T)}{q(\bm{x}_T|\bm{x}_{T-1})} ] + \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} [\sum_{t=1}^{T-1} \log \frac{p(\bm{x}_{t}| \bm{x}_{t+1}; \theta)}{q(\bm{x}_{t}|\bm{x}_{t-1})}] \\ &= \mathbb{E}_{q(\bm{x}_{1}|\bm{x}_0)}[\log p(\bm{x}_0|\bm{x}_1; \theta)] + \mathbb{E}_{q(\bm{x}_{T-1:T}|\bm{x}_0)} [\log \frac{p(\bm{x}_T)}{q(\bm{x}_T|\bm{x}_{T-1})} ] + \sum_{t=1}^{T-1} \mathbb{E}_{q(\bm{x}_{t-1:t+1}|\bm{x}_0)} [\log \frac{p(\bm{x}_{t}| \bm{x}_{t+1}; \theta)}{q(\bm{x}_{t}|\bm{x}_{t-1})}] \\ &= \underbrace{\mathbb{E}_{q(\bm{x}_{1}|\bm{x}_0)}[\log p(\bm{x}_0|\bm{x}_1; \theta)]}_{\text{reconstruction term}} \\ &\quad - \underbrace{\mathbb{E}_{q(\bm{x}_{T-1}|\bm{x}_0)} \Big \{ \mathbf{KL}(q(\bm{x}_T|\bm{x}_{T-1}) \| p(\bm{x}_T))}_{\text{prior matching term }} \Big \} \\ &\quad \quad - \underbrace{\sum_{t=1}^{T-1} \mathbb{E}_{q(\bm{x}_{t-1}, \bm{x}_{t+1}|\bm{x}_0)} \Big \{\mathbf{KL}(q(\bm{x}_t|\bm{x}_{t-1}) \| p(\bm{x}_t|\bm{x}_{t+1}); \theta) \Big \}}_{ \text{ consistency term } } \\ \end{array} \]注意到:
reconstruction term: 最大化这个即最小化重构损失;prior matching term: 最小化这个即最小化 \(q(\bm{x}_T|\bm{x}_{T-1})\) 和先验分布 \(p(\bm{x}_T)\) 的距离 (当然, 因为本身不包含 \(\theta\), 所以想要这个足够小, 就只有选择合适的 \(\beta_t\));consistency term: 最小化这个, 即要求两个序列在 \(\bm{x}_t, t=1,\ldots, T_1\) 处的分布是一致的.
-
通常, 我们为了估计上面的下界, 我们会用蒙特卡洛采样, 但是注意到 (12) 的 consistency 需要一次性采样 \(\bm{x}_{t-1}, \bm{x}_{t+1}\), 所以是极其不稳定的.
-
为此, 我们考虑引入 (9) 来解决这一问题.
\[\tag{13} \begin{array}{ll} \log p(\bm{x}_0) &= \log \int_{\bm{x}_{1:T}} d \bm{x}_{1:T} \: p(\bm{x}_{0:T}; \theta) \\ &= \log \int_{\bm{x}_{1:T}} d \bm{x}_{1:T} \: \frac{p(\bm{x}_{0:T}; \theta) \cdot q(\bm{x}_{1:T}|\bm{x}_0)}{q(\bm{x}_{1:T}|\bm{x}_0)} \\ &= \log \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Big [\frac{p(\bm{x}_{0:T}; \theta) }{q(\bm{x}_{1:T}|\bm{x}_0)} \Big ] \\ &\ge \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \log \Big [\frac{p(\bm{x}_{0:T}; \theta)}{q(\bm{x}_{1:T}|\bm{x}_0)} \Big ] \leftarrow \text{ Jensen's Inequality } \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \log \Big [\frac{p(\bm{x}_T) \prod_{t=1}^T p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{\prod_{t=1}^T q(\bm{x}_{t}|\bm{x}_{t-1})} \Big ] \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \log \Big [ \frac{p(\bm{x}_T) p(\bm{x}_{0}|\bm{x}_1; \theta) \prod_{t=2}^T p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)} {q(\bm{x}_1|\bm{x}_0)\prod_{t=2}^T q(\bm{x}_{t}|\bm{x}_{t-1}, x_0)} \Big ] \: \leftarrow \text{ 马氏性 } \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Bigg\{ \log \frac{p(\bm{x}_T)p(\bm{x}_0|\bm{x}_1; \theta)}{q(\bm{x}_1|\bm{x}_{0})} +\sum_{t=2}^{T} \log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{q(\bm{x}_{t}|\bm{x}_{t-1}, \bm{x}_0)} \Bigg \} \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Bigg\{ \log \frac{p(\bm{x}_T)p(\bm{x}_0|\bm{x}_1; \theta)}{q(\bm{x}_1|\bm{x}_{0})} +\sum_{t=2}^{T} \log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{\frac{q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0) q(\bm{x}_t| \bm{x}_0)}{q(\bm{x}_{t-1}|\bm{x}_0)}} \Bigg \} \: \leftarrow (9) \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Bigg\{ \log \frac{p(\bm{x}_T)p(\bm{x}_0|\bm{x}_1; \theta)}{q(\bm{x}_1|\bm{x}_{0})} +\sum_{t=2}^{T} \log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0)} +\sum_{t=2}^T \log \frac{q(\bm{x}_{t-1}|\bm{x}_0)}{q(\bm{x}_t|\bm{x}_0)} \Bigg \} \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Bigg\{ \log \frac{p(\bm{x}_T)p(\bm{x}_0|\bm{x}_1; \theta)}{q(\bm{x}_1|\bm{x}_{0})} +\sum_{t=2}^{T} \log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0)} +\log \frac{q(\bm{x}_{1}|\bm{x}_0)}{q(\bm{x}_T|\bm{x}_0)} \Bigg \} \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Bigg\{ \log \frac{p(\bm{x}_T)p(\bm{x}_0|\bm{x}_1; \theta)}{q(\bm{x}_1|\bm{x}_{0})} +\log \frac{q(\bm{x}_{1}|\bm{x}_0)}{q(\bm{x}_T|\bm{x}_0)} +\sum_{t=2}^{T} \log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0)} \Bigg \} \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} \Bigg\{ \log \frac{p(\bm{x}_T)p(\bm{x}_0|\bm{x}_1; \theta)}{q(\bm{x}_T|\bm{x}_{0})} +\sum_{t=2}^{T} \log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0)} \Bigg \} \\ &= \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)}[\log p(\bm{x}_0|\bm{x}_1; \theta)] +\mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} [\log \frac{p(\bm{x}_T)}{q(\bm{x}_T|\bm{x}_0)}] +\sum_{t=2}^T \mathbb{E}_{q(\bm{x}_{1:T}|\bm{x}_0)} [\log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0)} ] \\ &= \mathbb{E}_{q(\bm{x}_{1}|\bm{x}_0)}[\log p(\bm{x}_0|\bm{x}_1; \theta)] +\mathbb{E}_{q(\bm{x}_{T}|\bm{x}_0)} [\log \frac{p(\bm{x}_T)}{q(\bm{x}_T|\bm{x}_0)}] +\sum_{t=2}^T \mathbb{E}_{q(\bm{x}_{t-1:t}|\bm{x}_0)} [\log \frac{p(\bm{x}_{t-1}| \bm{x}_{t}; \theta)}{q(\bm{x}_{t-1}|\bm{x}_t, \bm{x}_0)} ] \\ &= \underbrace{\mathbb{E}_{q(\bm{x}_{1}|\bm{x}_0)}[\log p(\bm{x}_0|\bm{x}_1; \theta)]}_{-\mathcal{L}_{1} \text{ reconstruction term}} \\ &\quad - \underbrace{\mathbf{KL}(q(\bm{x}_T|\bm{x}_{0}) \| p(\bm{x}_T))}_{\mathcal{L}_{0} \text{ prior matching term }} \\ &\quad \quad - \underbrace{\sum_{t=2}^{T} \mathbb{E}_{q(\bm{x}_{t}|\bm{x}_0)} \Big \{\mathbf{KL}(q(\bm{x}_{t-1}|\bm{x}_{t}, \bm{x}_0) \| p(\bm{x}_{t-1}|\bm{x}_{t}; \theta) \Big \}}_{\mathcal{L}_{2:T} \text{ consistency term } } \\ \end{array} \]
各损失的设计与处理
现在我们已经有了
piror matching term
-
这实际上是统一前向的过程. 给定 \(p(\bm{x}_0)\), \(q(\bm{x}_{1:T}|\bm{x}_0) = \prod_{t=1}^T q(\bm{x}_t|\bm{x}_{t-1})\), 我们实际上已经确定了联合分布
\[q(\bm{x}_{0:T}), \]自然也就确定了边际分布
\[q(\bm{x}_T). \] -
但是比较尴尬的是, 我们已经提前确定好了先验分布 \(p(\bm{x}_T) = \mathcal{N}(\bm{0}; I)\) (因为它好采样), 所以我们是需要 \(q(\bm{x}_T) \approx p(\bm{x}_T)\) 来保证一个和谐统一的. \(\mathcal{L}_0\) 大体上就是做的这么一个事情.
-
DDPM 通过设计合适的 \(\beta_t\) 来使得 \(\mathcal{L}_0\) 比较小.
-
由 (6) (7) 可知:
\[\tag{14} q(\bm{x}_t|\bm{x}_0) \Leftrightarrow \mathcal{N}(\bm{x}_t; \Big [\prod_{s=1}^t \sqrt{1 - \beta_s}\Big] \bm{x}_0, \Big [1 - \prod_{s=1}^t (1 - \beta_s)\Big] \: I) \Leftrightarrow \mathcal{N}(\bm{x}_t; \sqrt{\bar{\alpha}_t} \bm{x}_0, (1 - \bar{\alpha}_t) I). \] -
既然我们希望它接近标准正态分布, 这就意味着
\[\bar{\alpha} \rightarrow 0. \] -
我们惊奇地发现, 只要 \(\beta_t \in (0, 1)\), 且步数 \(T\) 足够多, 这个条件总是能够被满足的. 当然一个较小的 \(\beta_t\) 容易更快的收敛 (但这不意味着反向的过程是更快的).
-
这一步的完成预告我们成功地完成且固定了联合分布 \(q(\bm{x}_{0:T})\) (而且边际分布满足我们的要求), 而我们接下来所要做的, 仅仅是通过一些方法来拟合这个联合分布, 使得采样是便利的, 可能的.
-
需要注意的是, 也有 \(\beta_t\) 或 \(\alpha_t\) 是可训练的情况, 后面我们会介绍其中一种情况.
reconstruction term
- 这实际上是在要求我们反向的边界对齐 [3].
- 把 \(\bm{x}_1\) 看成是隐变量 \(\bm{z}\), 它的处理过程可以和 VAE 中的一样.
consistency term
-
对于 \(\mathcal{L}_t\), 它的处理其实和 VAE 中的就非常类似了.
-
我们假设建模 \(p(\bm{x}_{t-1}|\bm{x}_t; \theta)\) 为 \(\mathcal{N}(\bm{x}_{t-1}; \bm{\mu}_{\theta}(\bm{x}_t, t), \sigma_t^2 I)\), 即方差和 \(q\) 的是一致的 (也有用学习的或者说插值的方法来玩的 [14]);
-
不加推导地给出
\[\tag{15} \mathbf{KL}(\mathcal{N}(\bm{x}; \bm{\mu}, \Sigma) \| \mathcal{N}(\bm{x}; \bm{\mu}', \Sigma') =\frac{1}{2}\Bigg[ \log\frac{|\Sigma'|}{|\Sigma|} - d + \text{tr}({\Sigma'}^{-1}\Sigma) +(\bm{\mu}' - \bm{\mu})^T {\Sigma'}^{-1} (\bm{\mu}' - \bm{\mu}). \Bigg] \] -
故
\[\tag{16} \begin{array}{ll} \mathcal{L}_t &\approx \mathbf{KL}(q(\bm{x}_{t-1}|\bm{x}_{t}, \bm{x}_0) \| p(\bm{x}_{t-1}|\bm{x}_{t}; \theta) \\ &\Leftrightarrow \frac{1}{2\sigma_t^2} \|\bm{\mu}_{\theta}(\bm{x}_t, t) - \bm{\mu}_t(\bm{x}_t, \bm{x}_0)\|_2^2, \end{array} \]此处的等价是指我们移除了和 \(\theta\) 无关的元素.
-
既然根据 (10) 可知:
\[\tag{17} \bm{\mu}_t(\bm{x}_t, \bm{x}_0) = \frac{\sqrt{\bar{\alpha}_{t-1}}(1 - \alpha_t) \bm{x}_0 + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})\bm{x}_t}{1 - \bar{\alpha}_t}, \]且对于 \(\bm{\mu}_{\theta}(\bm{x}_t, t)\), \(\bm{x}_t\) 也是可用的, 那么为了更好的用 \(\bm{\mu}_{\theta}(\bm{x}_t, t)\) 逼近 (16), 我们完全可以令
\[\bm{\mu}_{\theta}(\bm{x}_t, t) = \frac{\sqrt{\bar{\alpha}_{t-1}}(1 - \alpha_t) \bm{x}_{\theta}(\bm{x}_t, t) + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})\bm{x}_t}{1 - \bar{\alpha}_t}, \]然后直接用网络来得到 \(\bm{x}_{\theta}(\bm{x}_t, t)\) 并去拟合 \(\bm{x}_0\).
此时我们可以得到\[\tag{18} \mathcal{L}_t \approx \frac{1}{2\sigma_t^2} \frac{\bar{\alpha}_{t-1} (1 - \alpha_t)^2}{(1 - \bar{\alpha_t})^2} [\|\bm{x}_{\theta}(\bm{x}_t, t) - \bm{x}_0\|_2^2]. \]
Consistency term 的不同理解
通过不同角度, 我们可以对不同版本 consistency term, 这有助于我们从不同的角度去理解 DPM.
Signal-to-noise ratio (SNR)
-
我们可以从信噪比 SNR [8] 去理解 consistency term.
-
我们来仔细看看 (17) 中的系数:
\[\tag{19} \begin{array}{ll} \frac{1}{2\sigma_t^2} \frac{\bar{\alpha}_{t-1} (1 - \alpha_t)^2}{(1 - \bar{\alpha_t})^2} &=\frac{1}{2\frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}} \frac{\bar{\alpha}_{t-1} (1 - \alpha_t)^2}{(1 - \bar{\alpha_t})^2} \: \leftarrow (10) \\ &=\frac{1 - \bar{\alpha}_t}{2(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})} \frac{\bar{\alpha}_{t-1} (1 - \alpha_t)^2}{(1 - \bar{\alpha_t})^2} \\ &=\frac{1}{2} \frac{\bar{\alpha}_{t-1} (1 - \alpha_t)}{(1 - \bar{\alpha}_{t-1})(1 - \bar{\alpha_t})} \\ &=\frac{1}{2} \frac{\bar{\alpha}_{t-1}(1 - \bar{\alpha}_t) - \bar{\alpha}_t(1 - \bar{\alpha}_{t-1})}{(1 - \bar{\alpha}_{t-1})(1 - \bar{\alpha_t})} \\ &=\frac{1}{2} \Bigg \{\frac{\bar{\alpha}_{t-1}}{1 - \bar{\alpha}_{t-1}} - \frac{\bar{\alpha}_{t}}{1 - \bar{\alpha}_{t}} \Bigg \}. \end{array} \] -
注意到, \(q(\bm{x}_t|\bm{x}_0) \Leftrightarrow \mathcal{N}(\bm{x}_t; \sqrt{\bar{\alpha}}\bm{x}_0, (1 - \bar{\alpha}_t) I)\), 所以根据信噪比的定义 (\(\mu/\sigma\) 似乎更为常见):
\[\tag{20} \text{SNR} = \frac{\mu^2}{\sigma^2}. \] -
故实际上这个系数为
\[\tag{21} \frac{1}{2} (\text{SNR}_{t-1} - \text{SNR}_t), \]其中
\[\text{SNR}_t = \frac{\bar{\alpha}_t}{1 - \bar{\alpha}_t}. \] -
我们知道, 前向过程是一个加噪的过程, 所以 \(\text{SNR}_t\) 是随着 \(t\) 递减的. 所以有的人就想 [8], 我们不要人为地给定 \(\alpha_t\) 了, 让我们也来学习它吧. 于是把 \(\text{SNR}_t\) 构建成
\[\tag{22} \text{SNR}(t) = \exp(-\omega_{\eta}(t)) \]的形式了. 其中 \(\omega(\cdot)\) 是一个关于 \(t\) 单调递增的网络, \(\eta\) 是它的参数.
-
于是
\[\tag{23} \bar{\alpha}_t = \text{sigmoid}(-\omega_{\eta}(t)), \\ 1 - \bar{\alpha}_t = \text{sigmoid}(\omega_{\eta}(t)). \\ \]
第二种
-
根据 (10):
\[\tag{24} \bm{\mu}_t (\bm{x}_t, \bm{x}_0) = \frac{\sqrt{\bar{\alpha}_{t-1}}(1 - \alpha_t) \bm{x}_0 + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})\bm{x}_t}{1 - \bar{\alpha}_t}, \]以及
\[\tag{25} \bm{x}_t = \sqrt{\bar{\alpha}} \bm{x}_0 + \sqrt{1 - \bar{\alpha}} \bm{\epsilon} \Rightarrow \bm{x}_0 = \frac{\bm{x}_t - \sqrt{1 - \bar{\alpha}_t} \bm{\epsilon}}{\sqrt{\bar{\alpha}}}. \] -
故代入 (25) 到 (24) 中容易得到
\[\tag{26} \bm{\mu}_t(\bm{x}_t, \bm{x}_0) = \frac{1}{\sqrt{\alpha_t}} \bm{x}_t - \frac{1- \alpha_t}{\sqrt{1 - \bar{\alpha}_t} \sqrt{\alpha_t}} \bm{\epsilon}. \] -
倘若反向过程我不是直接拟合 \(\bm{x}_{\theta}(\bm{x}_t, t)\) 而是拟合 \(\bm{\epsilon}_{\theta}(\bm{x}_t, t)\), 则 (17) 变成
\[\tag{27} \mathcal{L}_t \approx \frac{1}{2\sigma_t^2} \frac{(1 - \alpha_t)^2}{\alpha_t (1 - \bar{\alpha_t})} [\|\bm{\epsilon}_{\theta}(\bm{x}_t, t) - \bm{\epsilon}\|_2^2]. \] -
其实这一种形态才是 DDPM 所推荐的形态, 而且似乎这种方式效果更佳.
采样
-
我们先来稍稍讲一下采样的事情.
-
既然
\[\tag{28} p(\bm{x}_{t-1}; \bm{x}_t; \theta) \Leftrightarrow \mathcal{N}(\bm{x}_{t-1}; \bm{\mu}_{\theta}(\bm{x}_t, t), \sigma_t^2 I). \]这里 \(\bm{\mu}_{\theta}\) 可以是直接拟合, 也可以是通过 \(\bm{x}_{\theta}\) 拟合, 也可以通过残差 \(\bm{\epsilon}_{\theta}\) 拟合.
-
那么自然地
\[\tag{29} \bm{x}_{t-1} = \bm{\mu}_{\theta}(\bm{x}_t, t) + \sigma_t \bm{z}, \quad \bm{z} \sim \mathcal{N}(\bm{0}, I), \quad t=1,2,\ldots T. \] -
具体地:
- 对于 (17):
\[\tag{29} \bm{\mu}_{\theta}(\bm{x}_t, t) = \frac{\sqrt{\bar{\alpha}_{t-1}}(1 - \alpha_t) \bm{x}_{\theta}(\bm{x}_t, t) + \sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})\bm{x}_t}{1 - \bar{\alpha}_t}; \]- 对于 (27):
\[\tag{30} \bm{\mu}_t(\bm{x}_{t}, t) = \frac{1}{\sqrt{\alpha_t}} \bm{x}_t - \frac{1- \alpha_t}{\sqrt{1 - \bar{\alpha}_t} \sqrt{\alpha_t}} \bm{\epsilon}_{\theta}(\bm{x}_t, t). \] -
其实还有一个问题, 就是我们必须循规蹈矩地按照前向地过程反向地来一遍吗? 其实是不用的, 甚至 \(t\) 都不一定需要精准匹配前向过程, 只是此时我们需要估计 \(\alpha_t\) (如果不是可学习的话), 可以通过插值等方法实现 [14].
Score Matching
在引出最后的 score-based DPM 前, 让我们首先了解 score matching [10].
我们可以用
来表示任意的分布? 其中 \(f_{\theta}(\bm{x})\) 通常被称为是 energy function, 鼎鼎大名的能量函数. 这种定义有什么好处呢, 首先我们定义 score function 为:
有了它, 结合 Langevin dynamics 就可以进行采样了 (实际上这是一步没有接受概率部分的 LMC 采样)
其中 \(\eta\) 表示采样的步长.
容易知道, \(\mathcal{N}(\bm{\mu}, \sigma^2I)\) 的 score function 为
取步长 \(\eta = 2\sigma^2\), 可得
这其实和 (29) 的形式就非常一致了.
-
既然 score function 这么有用, 甚至有了 score function 就和知道了分布没什么本质区别, 那么我们可以直接拟合它不就好了. 于是目标就成了
\[\tag{33} \min_{\theta} \quad \frac{1}{2} \mathbb{E}_{p(\bm{x})}\Big [\|\bm{s}_{\theta}(\bm{x}) - \nabla_{\bm{x}} \log p(\bm{x})\|_2^2 \Big], \] -
但是我们不知道数据的分布 \(p(\bm{x})\) 自然也无法知道目标 \(\nabla_{\bm{x}}p(\bm{x})\), score matching 实际上就是解决这个问题, 它证明 (33) 实际上等价于
\[\tag{34} \min_{\theta} \quad \mathbb{E}_{p(\bm{x})}\Big [\text{tr}(\nabla_{\bm{x}}\bm{s}_{\theta}(\bm{x})) + \frac{1}{2} \|\bm{s}_{\theta}(\bm{x})\|_2^2 \Big], \]此时我们就可以用蒙特卡洛采样来近似了.
-
Denosing Score Matching 是一种更加鲁棒的 score matching, 他认为在实际中我们采样得到的数据处在一个低维的流形中, 故当我们采用
\[\tag{35} \min_{\theta} \quad \frac{1}{N} \sum_{i=1}^N \Big [\text{tr}(\nabla_{\bm{x}_i}\bm{s}_{\theta}(\bm{x}_i)) + \frac{1}{2} \|\bm{s}_{\theta}(\bm{x}_i)\|_2^2 \Big], \]来近似 (34) 的时候, 会导致 \(s_{\theta}(\bm{x})\) 在高密度的区域估计的比较好, 在低密度的区域估计的比较差. Denosing Score Matching 实际上是估计 \(q_{\sigma}(\tilde{\bm{x}}) = \int d\bm{x} \: q_{\sigma}(\tilde{\bm{x}}|\bm{x})p(\bm{x})\), 它实际上等价于
\[\tag{36} \min_{\theta} \: \frac{1}{2} \mathbb{E}_{q_{\sigma}(\tilde{\bm{x}}|\bm{x})p(\bm{x})} \Big[\|\bm{s}_{\theta}(\tilde{\bm{x}}) - \nabla_{\tilde{\bm{x}}} \log q_{\sigma}(\tilde{\bm{x}}|\bm{x}) \|_2^2 \Big]. \]借此, 我们可以期待 \(\bm{s}_{\theta^*}(\tilde{\bm{x}})\) 接近 \(\nabla_{\bm{\tilde{x}}} \log q_{\sigma}(\bm{\tilde{x}})\). 特别地, 当 \(\sigma\) 足够小的时候, 所得的 \(s_{\theta^*}(\bm{x}) \approx \nabla_{\bm{x}} \log p(\bm{x})\).
Score-based Generative Models
- 一种很有意思的观点是, 是把上述的离散的过程 \(k=0,1,\ldots, K\) 抽象为一个连续的随机过程.
- 首先需要声明一点, 假设我们考虑连续时间段 \([0, 1]\), 然后我们从中采样了一些点 \(t_0=0 < t_1 < \cdots < t_K = 1\) (这也是为啥上面我用 \(k\) 而非 \(t\) 表示的原因, 以免大家混淆). 更具体地, 取 \(t_k = \frac{k}{T}\).
- 现在, 我们将离散的过程连续化:
-
注意到 (DDPM 的前向扩散过程)
\[\tag{38} \bm{x}_{k} = \sqrt{1 - \beta_k} \bm{x}_{k-1} + \sqrt{\beta_k} \bm{z}_{k-1} \: \bm{z}_{k-1} \sim \mathcal{N}(\bm{0}, I). \] -
定义
\[\tag{39} \beta(t), \: t \in [0, 1] \]其满足
\[\tag{40} \beta(t_k) = T\beta_k. \] -
则 (38) 可以改写为
\[\tag{41} \begin{array}{ll} &\bm{x}_{k} = \sqrt{1 - \beta_k} \bm{x}_{k-1} + \sqrt{\beta_k} \bm{z}_{k-1} \: \bm{z}_{k-1} \sim \mathcal{N}(\bm{0}, I) \\ \Rightarrow& \bm{x}(t_k) - \bm{x}(t_{k-1}) = (\sqrt{1 - \beta(t_k)/T} - 1) \bm{x}(t_{k-1}) + \sqrt{\beta(t_k) / T} \bm{z}(t_{k-1}) \\ \Rightarrow& \bm{x}(t_k) - \bm{x}(t_{k-1}) = (\sqrt{1 - \beta(t_k)/T} - 1) \bm{x}(t_{k-1}) + \sqrt{\beta(t_k) / T} \bm{z}(t_{k}) \: \leftarrow \text{ 独立同分布 } \\ \Rightarrow& \bm{x}(t + \Delta t) - \bm{x}(t) = (\sqrt{1 - \beta(t + \Delta t)\Delta t} - 1) \bm{x}(t) + \sqrt{\beta(t + \Delta t)\Delta t} \bm{z}(t) \: \leftarrow \Delta t = \frac{1}{T} \\ \Rightarrow& d \bm{x}(t) = -\frac{1}{2}\beta(t) \bm{x}(t) dt + \sqrt{\beta}(t) d \bm{w} \: \leftarrow \Delta t \rightarrow 0. \end{array} \]这里 \(d\bm{w}\) 特指 Wiener process 中的增量, 既满足:
- \(\bm{w}(t + \Delta t) - \bm{w}(t) \sim \mathcal{N}(\bm{0}, \Delta t I)\);
- \(\bm{w}(t + \Delta t) - \bm{w}(t) \perp \!\!\! \perp \bm{w}(s), s < t\)
- \(\lim_{\Delta t \rightarrow 0} \bm{w}(t + \Delta t) = \bm{w}(t)\).
-
令 \(\bm{e}(t) := \mathbb{E}(\bm{x}(t))\), 根据 (39) 可知
\[\tag{42} \begin{array}{ll} &\bm{e}(t + \Delta t) - \bm{e}(t) = (\sqrt{1 - \beta(t + \Delta t)\Delta t} - 1)\bm{e}(t) + \bm{0} \\ \Rightarrow& d\bm{e}(t) = -\frac{1}{\beta(t)}\bm{e}(t) dt \\ \Rightarrow& \bm{e}(t) = \bm{e}_0 \bm{e}^{-\frac{1}{2}\int_{0}^t \beta (\tau) d\tau} \: \leftarrow 令 \: \bm{e}(0) = \bm{e}_0. \end{array} \]故 \(\bm{x}(t)\) 的条件期望为 \(\bm{e}_0 \bm{e}^{-\frac{1}{2}\int_{0}^t \beta (\tau) d\tau}\).
-
同理可得, \(\bm{x}(t)\) 的(条件)协方差 (给定起始值 \(\Sigma(0) = \Sigma_t\) 为
\[\tag{43} d \Sigma(t) = \beta(t) (I - \Sigma(t)) dt \Rightarrow \Sigma(t) = I + e^{-\int_0^t \beta(\tau) d\tau} (\Sigma_0 - I). \] -
在 \(\bm{e}(0) = \bm{\mu}_0 = \bm{x}_0, \Sigma(0) = \Sigma_0 = \bm{0}\) 的情况下:
\[\tag{44} q(\bm{x}(t)|\bm{x}_0) \Leftrightarrow \mathcal{N}(\bm{x}(t); \bm{x}_0 \bm{e}^{-\frac{1}{2}\int_{0}^t \beta (\tau) d\tau}, I - \bm{e}^{-\int_0^t \beta(\tau) d\tau} I), \]当 \(\int_0^t \beta(\tau) d \tau \rightarrow +\infty\) 的时候 (这实际上就是 DDPM 所设计的)
\[\tag{45} q(\bm{x}(t)|\bm{x}_0) \rightarrow \mathcal{N}(\bm{x}(t); \bm{0}, I). \]通常, 这种方差不发散的情况成为 variance preserving, 其实还有 variance exploding 的情况, 比如 SMLD [5].
-
此外, 特别注意到, \(e^{-\int_0^t \beta (\tau) d\tau}\) 和我们之前定义的 \(\text{SNR}(t) = e^{-\omega_{\eta}(t)}\)是如此相似.
-
一般化
-
上述的过程, 实际上是将 DPM 的扩散过程和一个 SDE 联系起来了, [7] 中给出了一个更加一般化的形式:
\[\tag{46} d\bm{x}(t) = \bm{\xi}(\bm{x}, t) dt + \bm{\kappa} (\bm{x}, t) d\bm{w}(t), \]其中
\[\tag{47} \bm{\xi}(\cdot, t): \mathbb{R}^{d} \rightarrow \mathbb{R}^d, \]代表均值的偏移程度,
\[\bm{\kappa}(\cdot, t): \mathbb{R}^{d} \rightarrow \mathbb{R}^{d \times d} \]服务于 Wiener 过程.
-
自然地, 我们可以通过指定不同 \(\bm{\xi}, \bm{\kappa}\) 来获得不同的 DPMs (当然, 前提是你能够据此推导出条件分布 \(q(\bm{x}_t|\bm{x}_0)\), 这样才能运用 (50) 来求解).
-
现在的问题是, 前向扩散过程如此描述了, 那逆向的过程怎么办呢? 幸运的是, 我们可以显式地给出 (43) 的逆过程
\[\tag{48} d\bm{x}(t) = \Bigg\{ \xi(\bm{x}, t) - [\nabla_{\bm{x}} \cdot [\bm{\kappa}(\bm{x}, t)\bm{\kappa}(\bm{x}, t)^T]] \bm{1}_d - \bm{\kappa}(\bm{x}, t)\bm{\kappa}(\bm{x}, t)^T \nabla_{\bm{x}} \log p(\bm{x}_t) \Bigg\} dt + \bm{\kappa}(\bm{x}, t) d \bm{w}. \] -
倘若我们利用 \(\bm{s}_{\theta^*}(\bm{x}_t, t)\) 比较好地估计了 \(\nabla_{\bm{x}} \log p(\bm{x}_t)\), 那么我们就可以利用一些数值方法去近似 (46) 了, 比如 (这个有很多的, 详情可以参考 [7])
\[\tag{49} \bm{x}_{t} = \bm{x}_{t+1} - \Bigg\{ \xi(\bm{x}_{t+1}) - [\nabla_{\bm{x}} \cdot [\bm{\kappa}(\bm{x}_{t+1})\bm{\kappa}(\bm{x}_{t+1})^T]] \bm{1}_d - \bm{\kappa}(\bm{x}, t)\bm{\kappa}(\bm{x}_{t+1})^T \bm{s}_{\theta*}(\bm{x}_{t+1}, t+1) \Bigg\} + \bm{\kappa}(\bm{x}_{t+1}) \bm{z}_{t+1}. \] -
此时我们可以发现, 我们所要做的就是通过 \(\bm{s}_{\theta}(\bm{x}_t, t)\) 来拟合 \(\nabla_{\bm{x}} \log p(\bm{x}_t)\), 这实际上是 denosing score matching 做的事情. 即
\[\tag{50} \begin{array}{ll} &\min_{\theta} \: \mathbb{E}_{p(\bm{x}_t)}\Big[ \|\bm{s}_{\theta}(\bm{x}_t, t) - \nabla_{\bm{x}} \log p(\bm{x}_t)\|_2^2 \Big] \\ \Leftrightarrow &\min_{\theta} \: \mathbb{E}_{p(\bm{x}_0) q(\bm{x}_t|\bm{x}_0)}\Big[ \|\bm{s}_{\theta}(\bm{x}_t, t) - \nabla_{\bm{x}} \log q(\bm{x}_t|\bm{x}_0)\|_2^2 \Big] \\ \Leftrightarrow &\min_{\theta} \: \mathbb{E}_{p(\bm{x}_0) q(\bm{x}_t|\bm{x}_0)}\Big[ \|\bm{s}_{\theta}(\bm{x}_t, t) - \frac{\bm{x}_0 - \bm{x}_t}{\sigma_t^2} \|_2^2 \Big]. \end{array} \]注: 这里的 \(\sigma_t\) 不是 (10) 中的, 是根据方程推导出来的条件分布 \(q(\bm{x}_t|\bm{x}_0)\), 此处我们取了一个条件分布恰好满足高斯分布的特例 (如 DDPM (42) 那样).
-
最后, 对于 score-based DPM 而言, 我们通常采用如下的损失
\[\tag{51} \min_{\theta} \: \sum_{t} \lambda_t \mathcal{L}_t(\theta), \]权重 \(\lambda_t\) 主要是用来平衡尺度的差异, 需要尽可能保持一致 [5].
条件生成模型
-
很多时候, 我们需要构建条件概率模型 \(p(\bm{x}| \bm{c})\) 并从中进行采样 [11, 12, 13, 14], 比如经典的 text-image [13];
-
一种直接的手段就是保持前向不变, 在后向的时候拟合条件概率分布:
\[\tag{52} p(\bm{x}_{0:T}|\bm{c}) = p(\bm{x}_T) \prod_{t=1}^T p(\bm{x}_{t-1}|\bm{x}_t, \bm{c}; \theta). \]对应不同的 DPMs, 就会需要拟合
\[\tag{53} \bm{\mu}_{\theta}(\bm{x}_t, \bm{c}, t), \bm{s}_{\theta}(\bm{x}_t, \bm{c}, t). \] -
比较困惑我的一个问题是, 为什么保持前向不变呢? 我是这般想的, 实际上我们应该采取如下的方案:
\[\tag{54} q(\bm{x}_{0:T}|\bm{c}) = p(\bm{x}_0|\bm{c}) \prod_{t=1}^T q(\bm{x}_{t}|\bm{x}_{t-1}, \bm{c}), \]但是因为前向扩散的过程导致 \(\bm{c} \rightarrow \bm{x}_0 \rightarrow \bm{x}_{t-1} \rightarrow \bm{x}_t\), 所以根据马氏性
\[\tag{55} q(\bm{x}_{t}|\bm{x}_{t-1}, \bm{c}) =q(\bm{x}_{t}|\bm{x}_{t-1}). \]所以前向过程的参数的推导啥的是不需要变的.
Classifier Guidance
-
首先我们根据 score-based DPMs 来推导如何利用额外的分类器来条件采样 [7].
-
注意到
\[\tag{56} \begin{array}{ll} \nabla_{\bm{x}_t} \log p(\bm{x}_t|y) &=\nabla_{\bm{x}_t} \log \frac{p(\bm{x}_t) p(y|\bm{x}_t))}{p(y)}\\ &=\underbrace{\nabla_{\bm{x}_t} \log p(\bm{x}_t)}_{\text{ unconditional score }} + \underbrace{\nabla_{\bm{x}_t} \log p(y|\bm{x}_t))}_{ \text{adversarial gradient} }. \\ \end{array} \]第一部分可以通过之前的方法拟合, 第二部分可以训练一个分类器 (如果可以的话). 更一般地, 可以通过
\[\tag{57} \underbrace{\nabla_{\bm{x}_t} \log p(\bm{x}_t)}_{\text{ unconditional score }} + \lambda \cdot \underbrace{\nabla_{\bm{x}_t} \log p(y|\bm{x}_t))}_{ \text{adversarial gradient} }. \]来控制多样性和准确性.
-
这种 Classifer Guidance 方法的好处就是, 我们可以在一个进行训练好的普通 DPM 上, 自己训练一个分类器, 然后引导采样即可.
-
不过这个分类器不同于一般的分类器, 它需要在 \(\bm{x}_t\) 这种被扰动的情况下也能正确估计 \(p(y|\bm{x}_t)\) 的能力, 这个可能不是那么容易做到的.
-
此外注意到, 这里我用了 \(y\) 而非向量 \(\bm{c}\), 因为后者的分类器就更加难以定义和衡量了.
Classifier-Free Guidance
-
很多时候 \(\bm{c}|\bm{x}_t\) 的分类器很难构造 (特别是需要针对从清楚到模糊的所有样本), 此时我们可以再绕一步回到起始 [11, 12]
\[\tag{58} \begin{array}{ll} \nabla_{\bm{x}_t} \log p(\bm{x}_t|\bm{c}) &\leftarrow (1 - \lambda) \underbrace{\nabla_{\bm{x}_t} \log p(\bm{x}_t)}_{\text{ unconditional score }} + \lambda \underbrace{\nabla_{\bm{x}_t} \log p(\bm{x}_t|\bm{c}))}_{ \text{conditional score} }. \\ \end{array} \]如此一来, 避免了分类器的构造, 而且可以通过调节 \(\lambda\) 来平衡多样性和准确性.
-
此外, 我们不需要训练两个单独的 DPMs (一个条件的, 一个非条件的), 实际上我们只需要拟合
\[\tag{59} \bm{\mu}_{\theta}(\bm{x}_t, \bm{c}, t), \]并假设
\[\tag{60} \bm{\mu}_{\theta}(\bm{x}_t, t)= \bm{\mu}_{\theta}(\bm{x}_t, \bm{c} = \empty, t), \]即可.
总结
我们首先回顾了 VAE, 和基于 Flow 的 VAE, 由此更好地理解基于 VAE 的 DPM, 它的 consistency term 的不同变种可以帮助我们更好地理解 DPM. 最后, 我们又从 SDE 的角度连续化了 DPM, 通过了解前向的扩散过程和后面显式的逆过程, 构建不同的 DPM 只需要注意 \(\bm{\xi}, \bm{\kappa}\) 的设计即可. 整个 Score-based DPM 的核心就是 \(\nabla_{\bm{x}} p(\bm{x}_t)\) 的拟合, 这用到了 Denosing Score Matching 的技巧.
最后, 让我们领略一下 DPM 的魅力吧.
