Perturbation-Recovery Method for Recommendation
概
本文将最近很火的 diffusion model 的思想用在推荐系统里, 不过体系是 ODE 的体系.
符号说明
-
\(\mathcal{U, V}\), users, items;
-
\(R \in \{0, 1\}^{\mathcal{|U| \times |V|}}\), 交互矩阵;
-
\(U = \text{Diag}(R\bm{1})\), user degree matrix;
-
\(V = \text{Diag}(\bm{1}^TR)\), item degree matrix;
-
\(\tilde{R} = U^{-1/2} R V^{-1/2}\);
-
\(\tilde{P} = \tilde{R}^T \tilde{R}\), normalized item-item 邻接矩阵;
-
对于微分方程 (ODE)
\[\bm{h}(t) = \bm{h}(0) + \int_0^t f(\bm{h}(t), t; \theta) dt, \]-
我们可以通过 Euler 方法来从 \(\bm{h}(0)\) 逐步逼近到 \(\bm{h}(T)\):
\[\bm{h}(t + s) = \bm{h}(t) + s \cdot f(\bm{h}(t), t; \theta), \]这里每一步的步长为 \(s\).
-
也可以用比如 fourth-order Runge–Kutta (RK4) 来近似 \(\bm{h}(T)\):
\[\bm{h}(t + s) = \bm{h}(t) + \frac{s}{6}(f_1 + 2f_2 + 2f_3 + f_4), \\ f_1 = f(\bm{h}(t), t; \theta), \\ f_2 = f(\bm{h}(t) + \frac{s}{2}f_1, t + \frac{s}{2}; \theta), \\ f_3 = f(\bm{h}(t) + \frac{s}{2}f_2, t + \frac{s}{2}; \theta), \\ f_4 = f(\bm{h}(t) + sf_3, t + s; \theta). \\ \]
-
一个基于 ODE 的统一框架
-
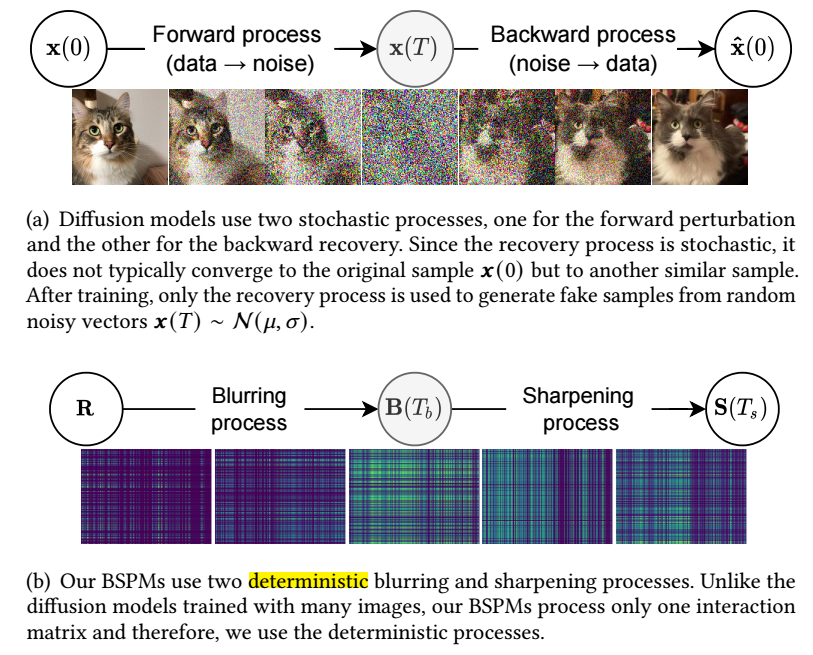
最近很火的 diffusion model, 如上图所示, 包含:
- 前向的加噪过程 (对应本文的模糊过程, blurring process);
- 后向的去噪过程 (对应本文的锐化过程, sharpening process);
-
具体来说, 它的形式如下 (具体请看这里 here):
-
前向:
\[d \bm{x} = f(\bm{x}, t) dt + g(t) d \bm{w}. \] -
后向
\[d \bm{x} = (f(\bm{x}, t) - g^2(t) \nabla_x \log p_t (\bm{x})) dt + g(t) d \bm{w}. \]
-
-
实际上, 在 GCN-based 的协同过滤上, 已经有很多工作在研究 blurring process 了, 比如 GF-CF:
\[\tag{1} \hat{R} = R (\tilde{P} + \beta V^{-\frac{1}{2}} \bar{U} \bar{U}^T V^{\frac{1}{2}}), \]这里 \(\bar{U}\) 是指 top-K 的奇异向量 (对应非常平滑的那部分).
-
我们可以将它纳入 ODE 的框架:
\[\tag{2} B(T_b) = B(0) + \int_{0}^{T_b} b(B(t)) dt, \]这里 \(b: \mathbb{R}^{\text{dim}(B)} \rightarrow \mathbb{R}^{\text{dim}(B)}\) 是提供模糊的函数.
当它为 GF-CF 所给定的形式, 即\[b_{GF-CF}(B(t)) = k B(t) (\tilde{P} + \beta V^{-\frac{1}{2}} \bar{U} \bar{U}^T V^{\frac{1}{2}} - I), \]通过 Euler 方法一步近似 (2) 的结果 (取 \(k=1, T_b=1\)) 恰恰为 (1).
我们还有一些其它能够提供模糊的函数:-
热扩散方程:
\[b_{HE}(B(t)) = k B(t) (\tilde{P} - I); \] -
Ideal low-pass filter:
\[b_{IDL}(B(t)) = B(t) (V^{-\frac{1}{2}} \bar{U} \bar{U}^T V^{\frac{1}{2}} - I). \]
-
-
现在我们已经构建好了 blurring process, 事实上之前的工作指出, 仅仅如此已经能够取得相当好的结果了. 但是, 这样的一种模糊的做法其实只能抓住 active 的用户的偏好, 对于细粒度的区分需要进一步尖化处理.
-
类似的, 我们构建
\[S(T_s) = S(0) + \int_{0}^{T_s} s(S(t)) dt, \]其中 \(s: \mathbb{R}^{\text{dim}(S)} \rightarrow \mathbb{R}^{\text{dim}(S)}\) 是具备锐化能力函数, 比如
\[s(S(t)) = -S(t) \tilde{P}. \]
BSPM
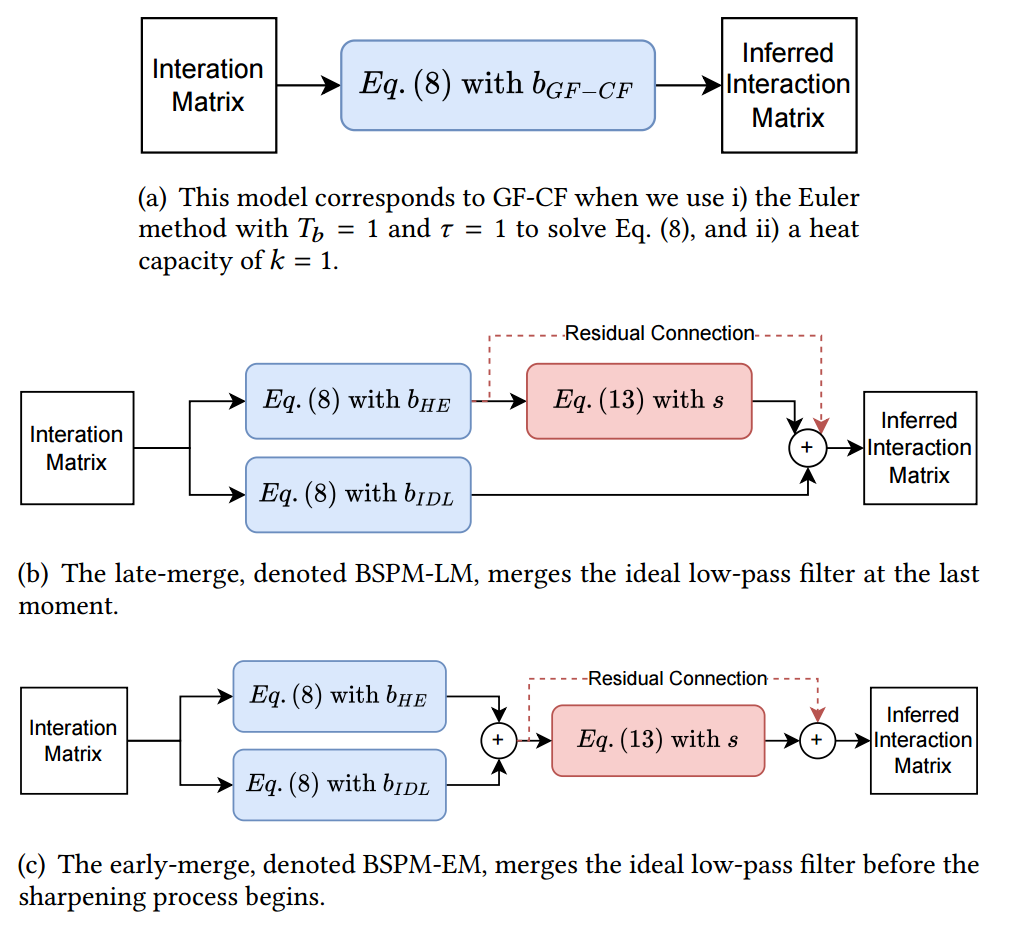
BSPM-LM
-
结构如上图 (b) 所示:
-
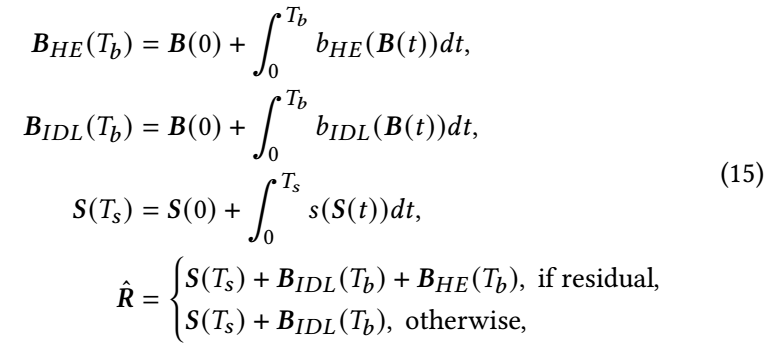
其中 \(B(0) = R, S(0) = B_{HE}(T_b)\), 即仅锐化由热扩散方程得到的部分.
BSPM-EM
- 结构如上图 (c) 所示:
- 其中 \(B(0) = R, S(0) = B_{HE}(T_b) + B_{IDL}(T_b)\), 即同时锐化热扩散方程和 IDL 所得到的部分.
注: 上面的 \(B(T_b)\) 以及 \(S(T_b)\) 都是通过 Euler, Runge-Kutta 或 Dormand–Prince (DOPRI) 等方法近似得到的解.
实验
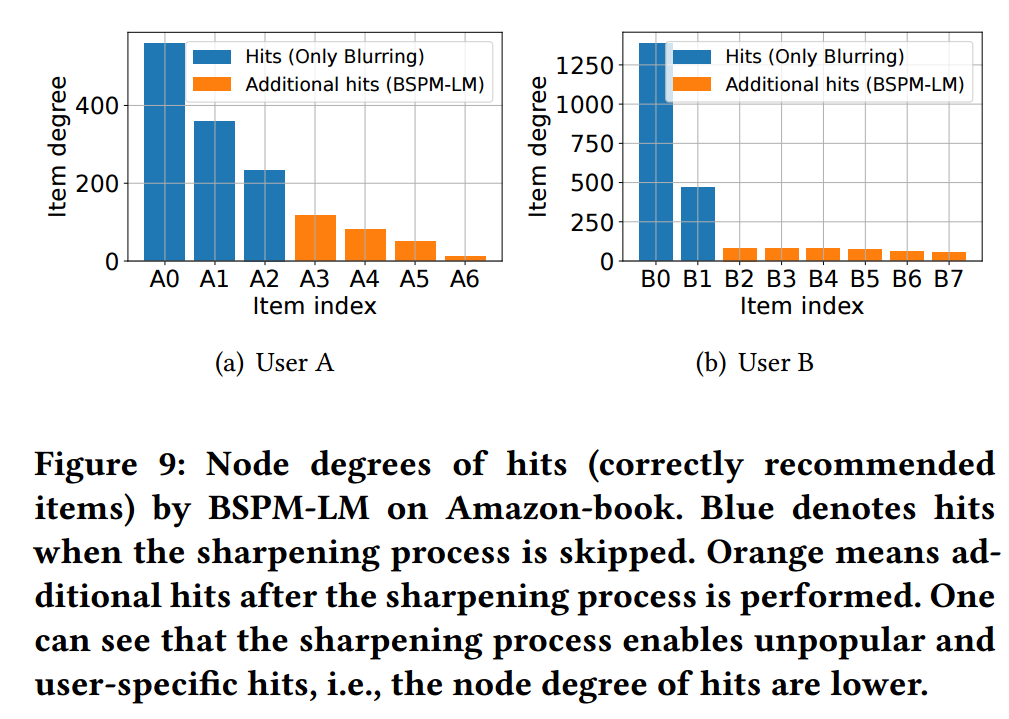
如上图所示, 作者比较了在进行锐化前后的变化. 可以发现, 锐化所得到的收益大都体现在那些不怎么热门的 items 上. 这是比较符合直觉的.
