Deoscillated Graph Collaborative Filtering
概
作者认为鉴于推荐数据集二部图的特点, 采用 GCN 的训练会产生 osciilation 的问题, 并采用 cross-hop 来解决.
符号说明
- \(\mathcal{G} = (\mathcal{V}, \mathcal{E})\), graph;
- \(A\), 邻接矩阵;
- \(\tilde{A} = D^{-1}A\);
- \(e_v^{(l)} \in \mathbb{R}^d\), hidden features of \(l\)-th layer;
- \(\mathcal{N}_v^{(k)}\), \(k\)-hop neighbors;
Motivation
-
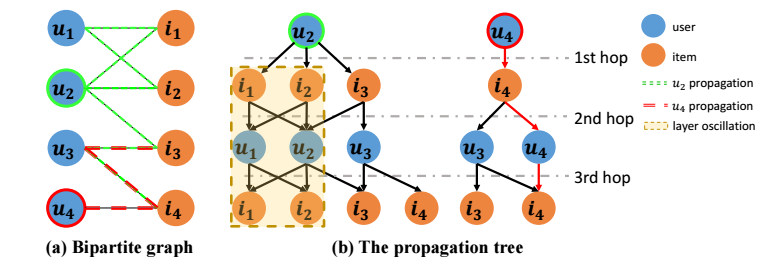
推荐数据集通常是二部图, user-item, 所以在此图上采用 GCN 它的更新方式如下图所示:
-
每一次 propagation 仅和 users 或 items 产生联系;
-
对于邻接矩阵 \(\tilde{A}\), 当 \(\mathcal{G}\) 是一个 regular (不可约, 非周期)的图时:
\[\lim_{t \rightarrow +\infty} \tilde{A}^tx_0 = \pi, \]但是这一性质对于二部图是不成立的. 所以作者认为, 直接采用二部图进行更新会有 osciilation 的问题.
本文思路
-
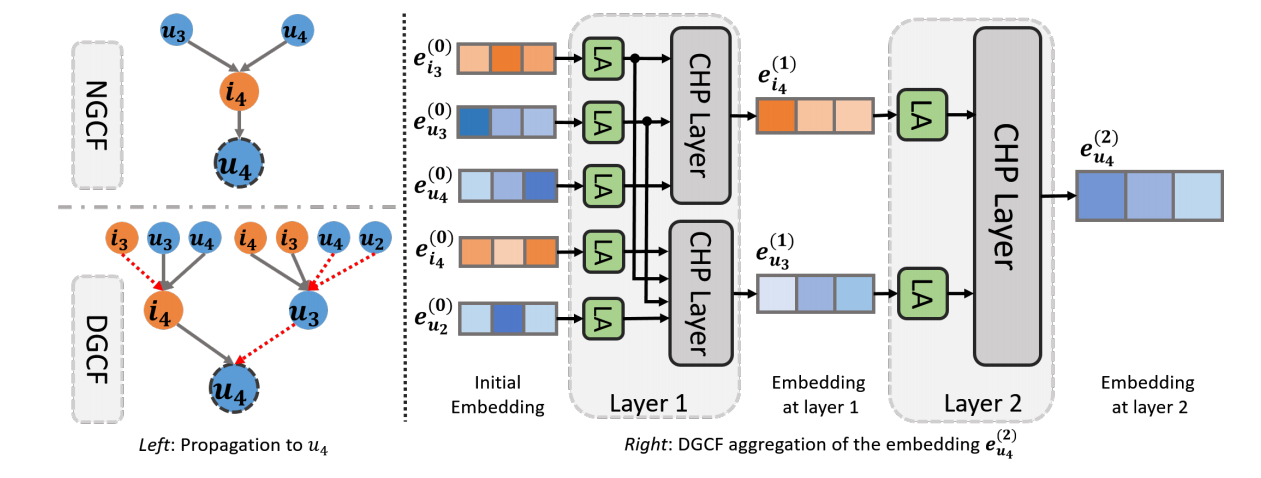
既然如此, 作者将 2-hop 邻居囊括进来用于更新:
-
首先通过 Locality-Adaptive Layer (LA layer) 对每一个结点的特征进行放缩
\[\tilde{E}^{(l)} = \Omega^{(l)} E^{(l)}, \\ \Omega^{(l)} = \text{diag}(\alpha^{(l)} \odot p) \in \mathbb{R}^{|\mathcal{V}| \times |\mathcal{V}|}. \]其中 \(\alpha^{(l)} \in [0, 1]^{|\mathcal{V}|}\) 是可训练的参数 (after sigmoid), \(p\) 是固定的参数;
-
令 \(C = A^2\), 定义:
\[\mathcal{L} = D^{-1/2} A D^{-1/2}, \: \mathcal{L}_c = D_c^{-1/2} C D_{c}^{-1/2}. \] -
然后
\[E^{(l)} = (\mathcal{L} + \mathcal{L}_c + I) \tilde{E}^{(l)}. \] -
最后的特征综合所有层的特征信息:
\[E^* = \frac{1}{L + 1} \sum_{l=0}^L E^{(l)}. \]
注: 实际上 \(\mathcal{L}_c\) 中有很多非常小的数, 这会带来很多的计算上的浪费, 故作者选择
\[\tilde{L}_c[i, j] =
\left \{
\begin{array}{ll}
\mathcal{L}_c[i, j] & \text{ if } \mathcal{L}_c[i, j] > \epsilon \\
0 & \text{otherwise} \\
\end{array}
\right ..
\]
注: 作者的实验结果有点奇怪, LightGCN 在 Gowalla 上的 NDCG@20 只有 0.1309, 不知道是不是数据处理不一样.
代码
[official]


