Visualizing Deep Neural Network Decisions: Prediction Difference Analysis
概
一种图像的可视化方法, 用到了 prediction difference analysis.
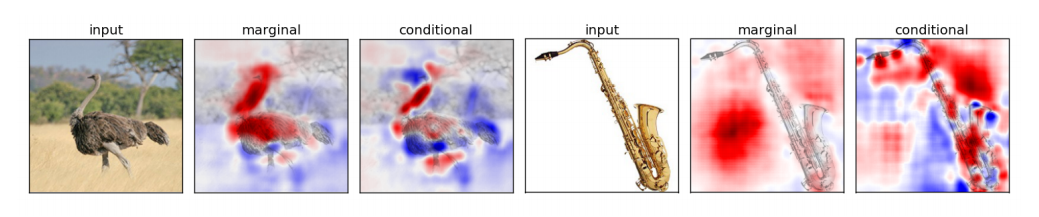
本文方法
-
给定一个图像 \(\bm{x}\), 我们想要探究其中的 \(x_i\) 元素特征的重要性;
-
我们希望用 \(p(c|\bm{x})\) 以及 \(p(c|\bm{x}_{\setminus i})\) 的差来表示, 倘若 \(\bm{x}\) 的真实标签为 \(c\), 那么差越大, 说明该特征越重要;
-
\(p(c|\bm{x}_{\setminus i})\) 可以利用下式进行估计
\[p(c|\bm{x}_{\setminus i}) = \sum_{x_i} p(x_i | \bm{x}_{\setminus i}) p(c|\bm{x}_{\setminus i}, x_i) \approx \sum_{x_i} p(x_i) p(c|\bm{x}_{\setminus i}, x_i), \]当我们认为 \(p(x_i | \bm{x}_{\setminus i}) \approx p(x_i)\) 的时候.
-
但很显然, 这个假设对于图像而言是非常不靠谱的, 所以作者采用的是如下的一个估计:
\[p(x_i|\bm{x}_{\setminus i}) \approx p(x_i| \bm{\hat{x}}_{\setminus i}), \]其中 \(\bm{\hat{x}}\) 是一个 \(l \times l\) 大小的包含 \(i\) 的 patch, 作者没说具体的估计方法 (我猜是从 \(\hat{\bm{x}}_{\setminus i}\) 里采样).
-
于是乎,
\[p(c|\bm{x}_{\setminus}) \approx \mathbb{E}_{x_i \sim p(x_i|\hat{\bm{x}}_{\setminus i})} [p(c|\bm{x}_{\setminus i}), x_i], \]我们可以从中采样 \(S\) 个点, 然后取平均估计.
-
之后, 作者定义
\[\text{WE}_i (c| \bm{x}) = \log_2 (\text{odds}(c|\bm{x})) - \log_2 (\text{odds}(c|\bm{x}_{\setminus i})), \]其中 \(\text{odds}(c|\bm{x}) = p(c|\bm{x}) / (1 - p(c|\bm{x}))\). \(\text{WE}\) 越大, 说明 \(x_i\) 越重要.
-
特别地, 改方法可以很容易推广到隐藏层中去.
注: 在实际中, 作者是对每个 \(k \times k\) patch 进行上述分析, 然后每个像素点的为所有包括该点的 patches 的重要性的平均.
代码
[official]
