EDITS: Modeling and Mitigating Data Bias for Graph Neural Networks
概
本文从 Attribute bias 和 Structural bias 两个角度为图数据本身去偏. 很有意思的想法.
Motivation
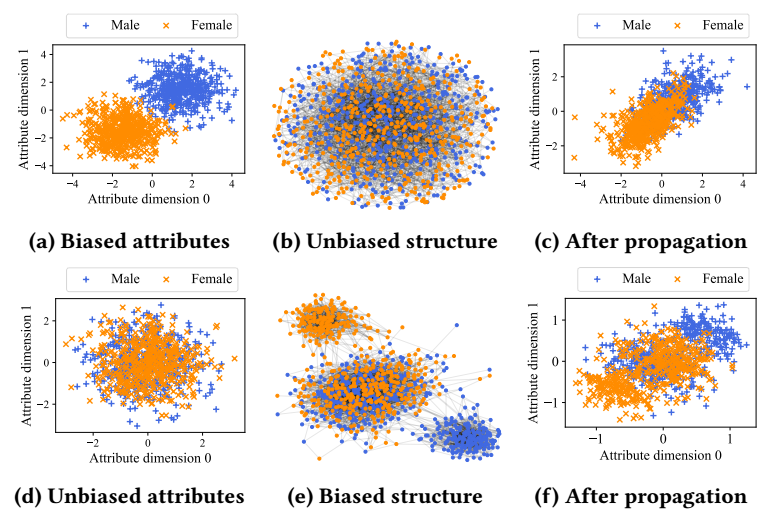
- 如上图所示, 作者首先用人工数据集来说明 attribute bias 和 structural bias 的存在和不同;
- 对于前者, 假设两个 group (Male, Female) 的特征分布是不同的 (如图 (a) 所示), 但是它们的图的结构是均匀的一致的, 此时经过 propagation 之后, attribute bias 实际上会有所缓解;
- 对于后者, 假设两个 group 的特征分布是一致的, 但是它们的图的结构是不一致的, 此时经过 propagation 之后的特征分布反而存在了 bias, 显然此 bias 是由 structural bias 引发的;
- 由此启发, 判断是否存在 attribute bias, 我们需要比较两个 group 的特征分布是否一致, 而为了判断是否存在 structural bias, 需要通过 propagation 后的特征分布的比较.
- 而本文的目标就是, 给定一个有偏的图 \(\mathcal{G} = (A, X)\), 来构造一个 \(\mathcal{\tilde{G}} = (\tilde{A}, \tilde{X})\) 来缓解 bias.
解决的思路
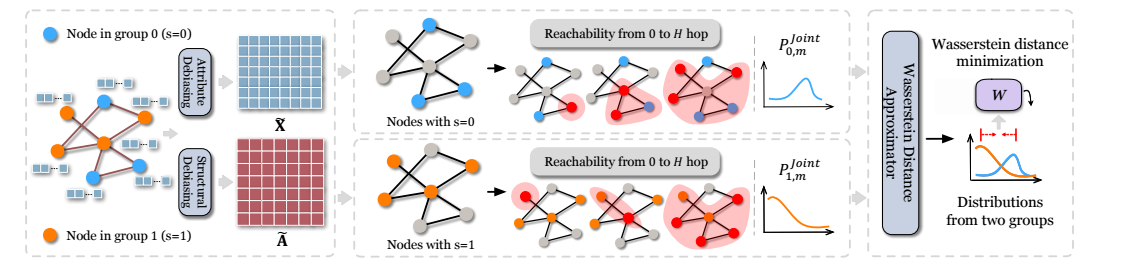
符号太多, 这里就讲一下作者的思路.
-
首先, 作者采用 Wasserstein distance, 即考察 propagation 前 (后) 的两个 group 的特征分布的差异, 用以衡量 attribute (structural) bias, 作者会用一些可训练的函数得到 \(\tilde{A}, \tilde{X}\);
-
其次, 因为 Wasserstein distance 很难直接优化, 所以就类似 W-GAN 一样, 作者先将这个分布距离问题转换为对偶问题, 这个对偶问题可以在 \(\|f\|_L \le k\) 的函数空间中优化:
\[\max_{\{f_m: 1 \le m \le M\} \subset \mathcal{F}} \mathscr{L}_1, \]其中 \(M\) 是特征的维度;
-
于是, 关于 \(\tilde{A}, \tilde{X}\) 的目标就是
\[\min_{\tilde{\Theta}, \tilde{A}} \: \mathscr{L}_1 + \mu_1 \|\tilde{X} - X\|_F^2 + \mu_2 \|\Theta\|_1 + \mu_3 \|\tilde{A} - A\|_F^2 + \mu_4\|\tilde{A}\|_1, \\ \]其中 \(\tilde{X}\) 是通过 \(\Theta\) 间接得到的. 上面的目标总结为:
- 去偏;
- 和原数据差距不能太远;
- 稀疏化.
-
虽然加了 \(\|\tilde{A}\|_1\), \(\tilde{A}\) 通常也不是非常稀疏的, 故作者实际上还用了截断.
代码
[official]
