Fairness without Demographics through Adversarially Reweighted Learning

目录

• 概
• 符号说明
• 本文方法
• 代码

Lahoti P., Beutel A., Chen J., Lee K., Prost F., Thain N., Wang X. and CHi E. H. Fairness without demographics through adversarially reweighted learning. In Advances in Neural Information Processing Systems (NIPS), 2020.

概

Rawlsian Max-Min Fairness: 假设 $H$ 是一个函数集合, 则其中最大化最小收益的元素 $h^*$ 称为满足 Rawlsian Max-Min fairness principle 的, 即:

$$\tag{1} h^* = \mathop{\text{argmax}} \limits_{h \in H} \min_{s \in S} U_{D_s}(h).$$

本文所关注的是, 在不知道 $S, \mathcal{D}_s$ 的前提下, 上述问题的一个可行性方案. 主要是利用了对抗训练的思想.

符号说明

• $\mathcal{D}$, 数据分布;
• $s \in S$, group;
• $U_{D_s}(h)$, group $s$ 在映射 $h$ 下的收益;

本文方法

• 我们用损失 $\mathcal{L}_{\mathcal{D}_s}(h) := \mathbb{E}_{(x_i, v_i) \sim \mathcal{D}_s} [\ell(h(x_i), y_i]$ 来定义效益:

  $$U_{\mathcal{D}_s}(h) = -\mathcal{L}_{\mathcal{D}_s}(h),$$

  此时

  $$\tag{3} h^* = \mathop{\text{argmin}} \limits_{h \in H} \max_{s \in S} \mathcal{L}_{D_s}(h).$$

• 进一步地, 将 (3) 转换为如下形式:

  $$\tag{4} \min_{\theta}\max_{\lambda} \sum_{s \in S} \lambda_s \mathcal{L}_{\mathcal{D}_s} (h) = \sum_{i=1}^n \lambda_{s_i} \ell(h(x_i), y_i);$$

  这是一个 $\theta, \lambda$ 的博弈的过程, 当然我们需要对 $\lambda$ 的形态加以限制, 否则它只会关注损失最大的那个 $s_i$;

• 因为我们是不知道 $S$ 的, 所以作者只是简单地进行了一个二分, 作者希望通过 $f_{\phi}: X \times Y \rightarrow [0, 1]$ 来指明那些损失很大的区域, 并且

  $$\lambda_{\phi}(x_i, y_i) = 1 + n \cdot \frac{f_{\phi}(x_i, y_i)}{\sum_{j=1}^n f_{\phi}(x_i, y_i)}.$$

• 需要注意的是, 这个重加权不是简单地为那些损失大的困难样本赋予更多的权重, $f_{\phi}$ 的输入是 $(x, y)$, 作者认为 group 和每个样本的特征 $(x, y)$ 是紧密相连的, 通过

  $$\max_{\phi} \: \sum_{i=1}^n \lambda_{\phi}(x_i, y_i) \ell(h(x_i), y_i),$$

  最终 $f_{\phi}$ 会将 $(x_i, y_i)$ 成功进行分组.

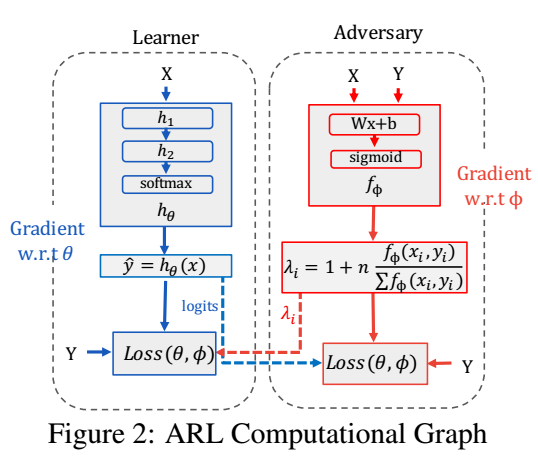
注: $f_{\phi}$ 作者仅仅用一层的 MLP 拟合.

代码

[official]