Robust Graph Convolutional Networks Against Adversarial Attacks

目录

• 概
• 符号说明
• 算法

Zhu D., Zhang Z., Cui P. and Zhu W. Robust graph convolutional networks against adversarial attacks. In ACM International Conference on Knowledge Discovery and Data Mining (KDD), 2019.

概

RGCN 设计了一种 Gaussian-based 的模块, 利用 Variance 来设计 attention 用于提高网络的鲁棒性. 从我的理解来看, 它提高对抗鲁棒性的能力堪忧.

符号说明

• $G = (V, E)$, 图;
• $V = \{v_1, \ldots, v_N\}$, nodes;
• $A$, 邻接矩阵;
• $\tilde{A}$, add self-loop;
• $\tilde{D}_{ii} = \sum_{j} \tilde{A}_{ij}$;
• $\bm{h}_i^{(l)}$, node $v_i$ 在第 $l$ 层的特征表示;
• $N(i) = \{v: (v, v_i) \in E\} \cup \{v_i\}$;
• $\odot$, element-wise 乘法;

算法

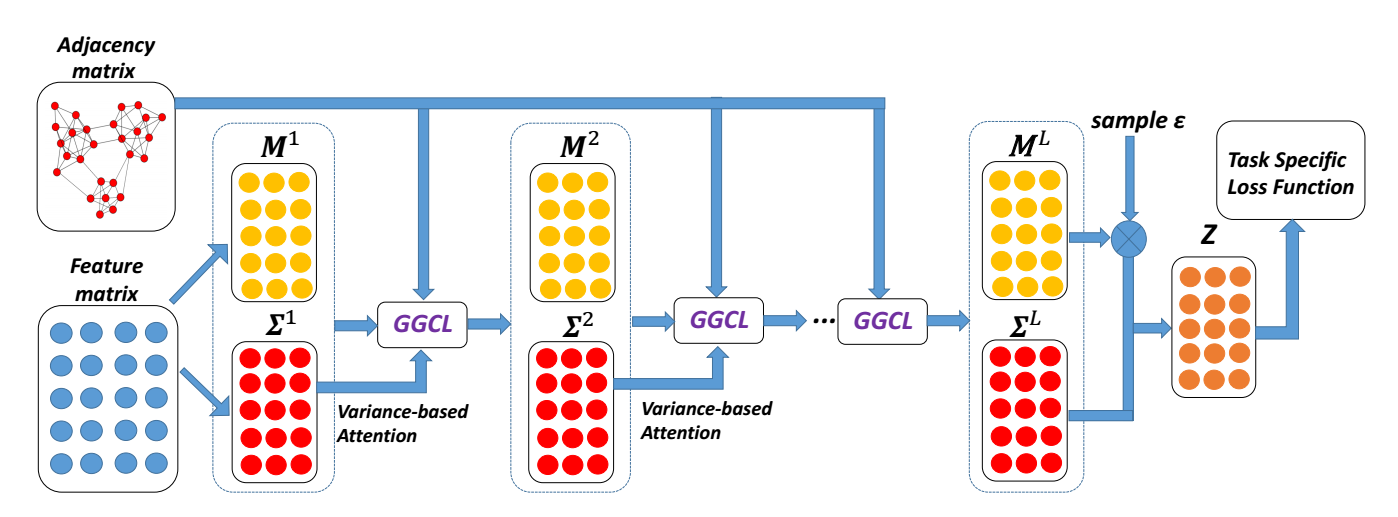
• 初始化均值和方差特征:

  $$M^{(0)} = [\bm{\mu}_1^{(0)}, \bm{\mu}_2^{(0)}, \ldots, \bm{\mu}_N^{(0)}]^T, \\ \Sigma^{(0)} = [\bm{\sigma}_1^{(0)}, \bm{\sigma}_2^{(0)}, \ldots, \bm{\sigma}_N^{(0)}]^T, \\ $$

  假设

  $$\bm{h}_i^{(0)} \sim \mathcal{N}(\bm{\mu}_i^{(0)}, \bm{\sigma}_i^{(0)});$$

• 第 $l$ 层进行如下操作:

  1. 首先计算 attention:

     $$\bm{\alpha}_j^{(l)} = \exp(-\gamma \bm{\sigma}_j^{(l - 1)}),$$

     可以看出, 方差越大对应的权重越小 (因为作者认为方差越大的越容易是噪声);

  2. 计算如下该层的均值和方差特征:

     $$\bm{\mu}_i^{(l)} = \rho(\sum_{j \in N(i)} \frac{\bm{\mu}_j^{(l-1)} \odot \bm{\alpha}_j^{(l)}}{\sqrt{\tilde{D}_{ii} \tilde{D}_{jj}}} W_{\mu}^{(l)}), \\ \bm{\sigma}_i^{(l)} = \rho(\sum_{j \in N(i)} \frac{\bm{\sigma}_j^{(l-1)} \odot \bm{\alpha}_j^{(l)} \odot \bm{\alpha}_j^{(l)}}{\sqrt{\tilde{D}_{ii} \tilde{D}_{jj}}}W_{\sigma}^{(l)});$$

     此时

     $$\bm{h}_i^{(l)} \sim \mathcal{N}(\bm{\mu}_i^{(l)}, \bm{\sigma}_i^{(l)});$$

  3. 用矩阵表示为如下结果:

     $$M^{(l)} = \rho(\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} (M^{(l-1)} \odot \mathcal{A}^{(l)}) W_{\mu}^{(l)}), \\ \Sigma^{(l)} = \rho(\tilde{D}^{-1/2} \tilde{A} \tilde{D}^{-1/2} (\Sigma^{(l-1)} \odot \mathcal{A}^{(l)} \odot \mathcal{A}^{(l)}) W_{\sigma}^{(l)});$$

• 最后一层, 我们得到最后的输出:

  $$\bm{z}_i = \bm{\mu}_i^{(L)} + \bm{\epsilon} \odot \sqrt{\bm{\sigma}_i^{(L)}}, \: \bm{\epsilon} \sim \mathcal{N}(\bm{0}, I);$$

• 最后通过如下损失进行训练:

  $$\mathcal{L} = \mathcal{L}_{cls} + \beta_1 \mathcal{L}_{reg1} + \beta_2 \mathcal{L}_{reg2},$$

  其中 $\mathcal{L}_{cls}$ 就是普通的分类损失 (基于 $\bm{z}_i$), 然后

  $$\mathcal{L}_{reg1} = \sum_{i=1}^N \text{KL}(\mathcal{N}(\bm{\mu}_i^{(1)}, \bm{\sigma_i}^{(1)}) \| \mathcal{N}(\bm{0}, I))$$

  确保第一层的输出是正态分布?

  $$\mathcal{L}_{reg2} = \|W_{\mu}^{(0)}\|_2^2 + \|W_{\sigma}^{(0)}\|_2^2$$

  为普通的对第一层的 L2 正则.