Releasing Graph Neural Networks with Differential Privacy Guarantees
概
PATE 提供了一种教师-学生的隐私保护机制, 但是这个机制依赖独立样本的划分, 这个对于图而言是比较难以实现的. 本文是 PATE 在图数据上的一个拓展.
符号说明
- \(G = (V, E)\), 图, 并以 \(G^{\dagger}\) 表示私有 (可能有隐私) 数据, \(G\) 表示公开的 (没有隐私风险的) 数据;
- \(X\), 点上的特征;
- \(\ell\)-hop 邻居:\[\mathcal{N}^{\ell}(v) = \{u| (u, w) \in E \text{ and } w \in \mathcal{N}^{\ell-1} (v) \}, \: \mathcal{N}^0(v) = \{v\}; \]
算法流程
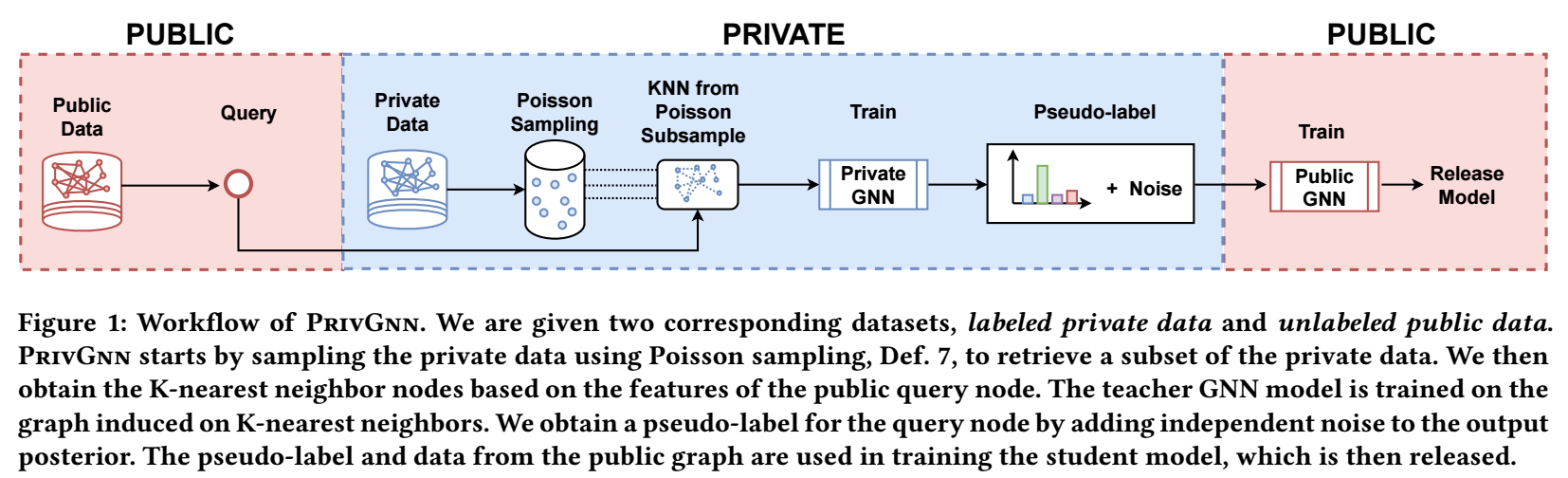
大体思路是为公开数据集的部分结点赋予伪标签, 然后用于训练.
-
私有图 \(G^{\dagger} = (V^{\dagger}, E^{\dagger})\) 和其结点上的特征 \(X^{\dagger}\); 无标签公开数据集 \(G\) 以及其上的特征 \(X\);
-
采样 \(Q \subset V\);
-
采样子集 \(\hat{V}^{\dagger} \subset V^{\dagger}\):
\[\tag{1} \hat{V}^{\dagger} = \{v_i | \sigma_i = 1, v_i \in V^{\dagger}, \sigma_i \sim \text{Bernoulli}(\gamma), \]其中 \(\gamma\) 是超参数;
-
对于每个 \(v \in Q\) 进行如下操作:
- 在 \(\hat{V}^{\dagger}\)中找到 \(v\) 的 \(K\) 近邻 \(V_{\text{KNN}}^{\dagger}(v)\), 并根据 \(G^{\dagger}\) 构建子图 \(H\);
- 初始化 GNN \(\Phi^{\dagger}\) 并在 \(H\) 利用私有数据标签 \(Y_{|H}^{\dagger}\) 进行训练;
- 通过如下方式计算 \(v\) 的伪标签:
\[\tag{2} \tilde{y}_v = \text{argmax} \{\Phi^{\dagger}(v) + \{\eta_1, \eta_2, \cdots, \eta_c\} \}, \: \eta_i \sim \text{Lap}(0, \beta); \] -
利用 \(G\), 以及伪标签 \(\tilde{Y} = \{\tilde{y}_v| v \in Q\}\) 训练 \(\Phi\).
注:
- 因为训练的时候不包含结点 \(v\), 所以这要求 GNN \(\Phi^{\dagger}\) 必须是 inductive 的, 比如 GraphSage;
- 该算法中引入了两个随机机制: Poisson 采样 (1) 和 拉普拉斯噪声 (2).
- 该算法的 bound 请回看原文.
