Semi-supervised Knowledge Transfer for Deep Learning from Private Training Data

目录

• 概
• 流程
• 理论分析
• 代码

Papernot N., Abadi M., Erlingsson U., Goodfellow I. and Talwar K. Semi-supervised knowledge transfer for deep learning from private training data. In International Conference on Learning Representations (ICLR), 2017.

概

本文 Private Aggregation of Teacher Ensembles (PATE) 介绍了一种防止私有数据泄露的方法.

流程

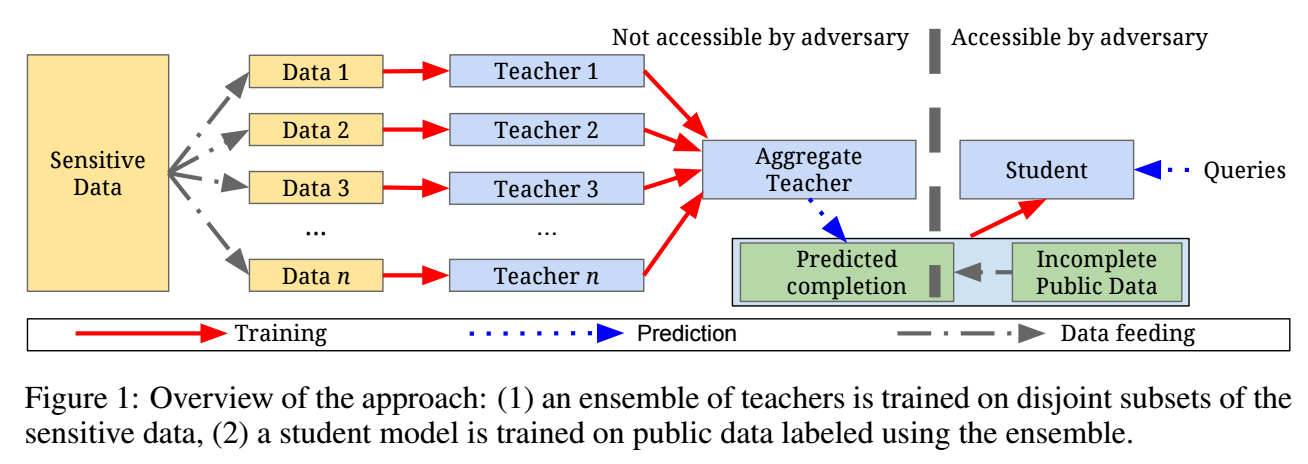
• 将敏感的私有数据 \((X, Y)\) 分割成 disjoint sets \((X_i, Y_i), i \in [n] = \{1,2,\ldots, n\}\);
• 每个子集训练一个教师网络 \(f_i(x), i \in [n]\);
• 将这些教师网络综合为 Aggregate Teacher \(f: \mathcal{X} \rightarrow [m]\), 对于任意的样本 \(x\), 它按照如下方式进行预测:
  1. 计算被预测为类别 \(j\) 的频次:
     \[n_j(x) := |\{i: i \in [n], f_i(x) = j\}|, \: j \in [m]; \]

  2. 采用如下方式预测:
     \[f(x) = \mathop{\text{argmax}} \limits_j \{n_j (x) + Lap (\frac{1}{\gamma})\}; \]
     其中 \(\gamma\) 是 privacy parameter, 控制隐私保护的效果, 显然越大的 \(\gamma\) 会有越好的隐私保护的效果, 但是伪标签的越不靠谱;
• 有了 \(f(\cdot)\) 之后, 我们可以在一个公开的数据集上进行训练, 我们首先为公开数据的部分数据通过 \(f(\cdot)\) 获得伪标签, 然后再通过半监督学习算法进行训练.

理论分析

这部分主要讲一下作者推导的思路.

定义1: 一个随机机制 \(\mathcal{M}: \mathcal{D} \rightarrow \mathcal{R}\) 是 \((\epsilon,\delta)\)-differential privacy 的, 如果对于任意的 \(d, d' \in \mathcal{D}, \rho(d, d') \le 1\) 以及输出子集 \(S \subset \mathcal{R}\) 有下列不等式成立:

\[\text{Pr}[\mathcal{M}(d) \in S] \le e^{\epsilon} \text{Pr}[\mathcal{M}(d') \in S] + \delta. \]

定义2: 令 \(aux\) 表示任意输入, 对于输出 \(o \in \mathcal{R}\), privacy loss 定义为:

\[c(o; \mathcal{M}, aux, d, d') := \log \frac{\text{Pr}(\mathcal{M}(aux, d) = o)}{\text{Pr}[\mathcal{M}(aux, d') = o]}. \]

并定义 privacy loss random variable 为

\[C(\mathcal{M}, aux, d, d') = c(\mathcal{M}(d); \mathcal{M}, aux, d, d'). \]

定义3: moments accountant 定义为:

\[\alpha_{\mathcal{M}}(\lambda) := \max_{aux, d, d'} \alpha_{\mathcal{M}} (\lambda; aux, d, d'), \]

其中

\[\alpha_{\mathcal{M}} (\lambda; aux, d, d') := \log \mathbb{E}[\exp(\lambda C(\mathcal{M}, aux, d, d'))]. \]

有了上面的定义, 还有下列的一些结果:

我们可以得到上述算法的一个的隐私保护的 bound.

• 这里作者说每一步是一个 \((2\gamma, 0)\)-DP, 经过 \(T\) steps 就是

  \[(4T\gamma^2 + 2\gamma \sqrt{2T\log \frac{1}{\delta}}, \delta)\text{-DP}, \]

  说实话, 我没怎么理解 每一步 的概念, 此外 differ by at most 1 in each corrdinate 这个条件我也不是很明了. 这里就大概讲一下上面的是怎么来的.

• 首先根据定理 2 得到

  \[\alpha(\lambda; axu, d, d') \le 2\gamma^2 \lambda(\lambda + 1); \]

• 然后根据定理 1 的 [Composability] 得到

  \[\alpha_{\mathcal{M}}(\lambda; d, d') = 2\gamma^2 T \lambda(\lambda+1); \]

• 接着

  \[\lambda^* = \text{argmin}_{\lambda} (\alpha_{\mathcal{M}}(\lambda) - \lambda\epsilon) = \frac{\epsilon - 2\gamma^2 T}{4\gamma^2 T}; \]

• 给定 \(\delta\), 理想的 \(\epsilon\) 需要满足:

  \[\delta = \exp(\alpha_{\mathcal{M}}(\lambda^*) - \lambda^* \epsilon), \]

  解得

  \[\epsilon = 2T\gamma^2 + 2\gamma \sqrt{2T\log \frac{1}{\delta}}, \]

  注意这里算出来的系数不一样, 不晓得是我哪里搞错了, 还是作者的笔误, 但是无伤大雅.

注: 3.3 中作者推了一个更 tight 的一个 bound, 这里不多赘述了.

代码

[official]