Beyond Homophily in Graph Neural Networks: Current Limitations and Effective Designs

目录

• 概
• 符号说明
  • Homophily and heterophily
• H2GCN
• 代码

Zhu J., Yan Y., Zhao L., Heimann M., Akoglu L. and Koutra D. Beyond homophily in graph neural networks: current limitations and effective designs. In Advances in Neural Information Processing Systems (NIPS), 2020.

概

算是一些 tricks 的综合性的工作 ?

符号说明

• \(\mathcal{G} = (\mathcal{V}, \mathcal{E})\), 图;
• \(A \in \mathbb{R}^{n \times n}\), 邻接矩阵;
• \(X \in \mathbb{R}^{n \times F}\), node features;
• \(L\), unnormalized graph Laplacian matrix;
• \(N(v)\), 1-hop neighbors;
• \(\bar{N}(v) = N(v) \setminus \{v\}\),
• \(N_i(v)\), \(i\)-hop neighbors;
• \(\bar{N}_i(v) = N_i(v) \setminus \{v\}\);

Homophily and heterophily

edge homophily ratio:

\[h = \frac{|\{(u, v): (u, v) \in \mathcal{E} \wedge y_u = y_v\}|}{|\mathcal{E}|}, \]

它衡量了边两端结点同属同一个类别的比例. 当 \(h \rightarrow 1\) 的时候, 我们称这个图是偏 homophily 的, 否则则这个图是偏 heterophily 的.

注意: heterophily 和常说的 Heterogeneity (异构图) 有点像, 后者描述的是一个图的结点的 type 不一致 (\(\ge 2\)), 比如一个图中存在 (users, watch, movies) 的关系. 前者描述了 group 的一个性质, 显然当 \(h \rightarrow 1\) 的时候, 不同的 groups 之间就很少产生联系, 这个时候进行 node 的分类是比较容易的.

H2GCN

• 作者说通常的 GNN 很难推广到 heterophily 的情形, 即 \(h \rightarrow 0\), 因为此时 edge 并不描述了我们通常认为的那种相关性, 下面是一个例子:

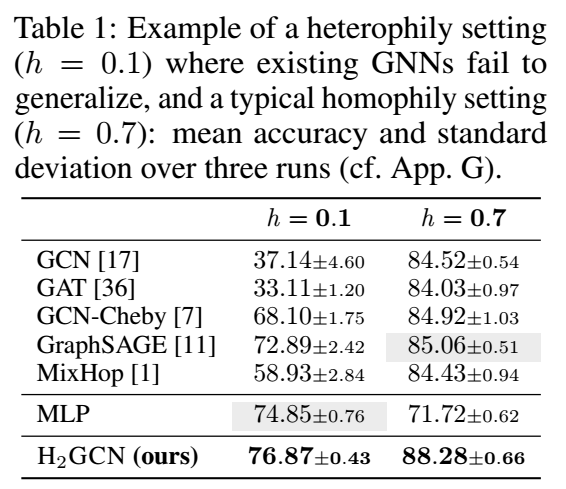
可以看到, 大部分 GNN 对于 \(h=0.7\) 即偏 homophily 的图比较擅长;

• 传统的 GNN 可以归纳为如下的结构:

  \[\bm{r}_v^{(k)} = f(\bm{r}_v^{(k-1)}, \{\bm{r}_u^{(k-1)}: u \in N(v)\}); \]

• 作者提出了三个改进的点:

  1. 采取如下形式:

     \[\bm{r}_v^{(k)} = \text{COMBINE}(\bm{r}_v^{(k-1)}, \text{AGGR}(\{\bm{r}_u^{(k-1)}: u \in \bar{N}(v)\})), \]

     作者认为, 每一次更新的时候, 不要把自身的 feature 和邻居的 feature 简单地通过例如平均地方式混合在一起, 可以采用比如 GraphSAGE 的 concatenation 的方式. 所以这里 \(\text{AGGR}(\cdot)\) 仅包括非自身的邻居;

  2. 进一步地, 直接加入 \(k-\)hop 的信息 (这里 \(k=2\)):

     \[\bm{r}_v^{(k)} = \text{COMBINE}(\bm{r}_v^{(k-1)}, \text{AGGR}(\{\bm{r}_u^{(k-1)}: u \in \bar{N}_1(v)\}), \text{AGGR}(\{\bm{r}_u^{(k-1)}: u \in \bar{N}_2(v)\})), \]

     作者认为, 虽然一阶的 edge 往往并不一定代表相似性, 高阶的 edge 往往是代表相似性的 (作者给出了一个特殊的证明), 所以直接引入 \(k\)-hop 的信息会有利于处理 heterophily 的情况;

  3. 在最后进行 node 分类的时候, 综合所有的层的信息:

     \[\bm{r}_v^{(\text{final})} = \text{COMBINE}(\bm{r}_v^{(1)}, \cdots, \bm{r}_v^{(K)}), \]

     这是因为随着层的加深, 这些特征逐渐由 local 的信息转到 global 的信息, 综合它们会有利于最后的分类.

• 综合来说, H2GCN 的流程如下:

  \[\bm{r}_v^{(k)} = \text{COMBINE}(\bm{r}_v^{(k-1)}, \text{AGGR}(\{\bm{r}_u^{(k-1)}: u \in \bar{N}_1(v)\}), \text{AGGR}(\{\bm{r}_u^{(k-1)}: u \in \bar{N}_2(v)\})), \]

  其中

  \[\bm{r}_v^{(k)} = [\bm{r}_{v, 1}^{(k)} \| \bm{r}_{v, 2}^{(k)}], \\ \bm{r}_{v, i}^{(k)} = \sum_{u \in \bar{N}_i(v)} \bm{r}_u^{(k-1)} d_{v, i}^{-1/2} d_{u, i}^{-1/2}. \]

  最后综合的时候

  \[\bm{r}_{v}^{(\text{final})} = [\bm{r}_v^{(0)} \| \bm{r}_v^{(1)} \| \cdots \| \bm{r}_v^{(K)}], \\ y_v = \text{argmax} \{\text{softmax} (\bm{r}_v^{(\text{final})} W_c \}. \]

代码

[official]