On the Bottleneck of Graph Neural Networks and Its Practical Implications
概
描述了 GNN 中纯在的 over-squashing 现象, 如下图所示, 虽然 GNN 的感受野能够很大, 但是与之交互的结点的信息流必须通过狭窄的路径传递.
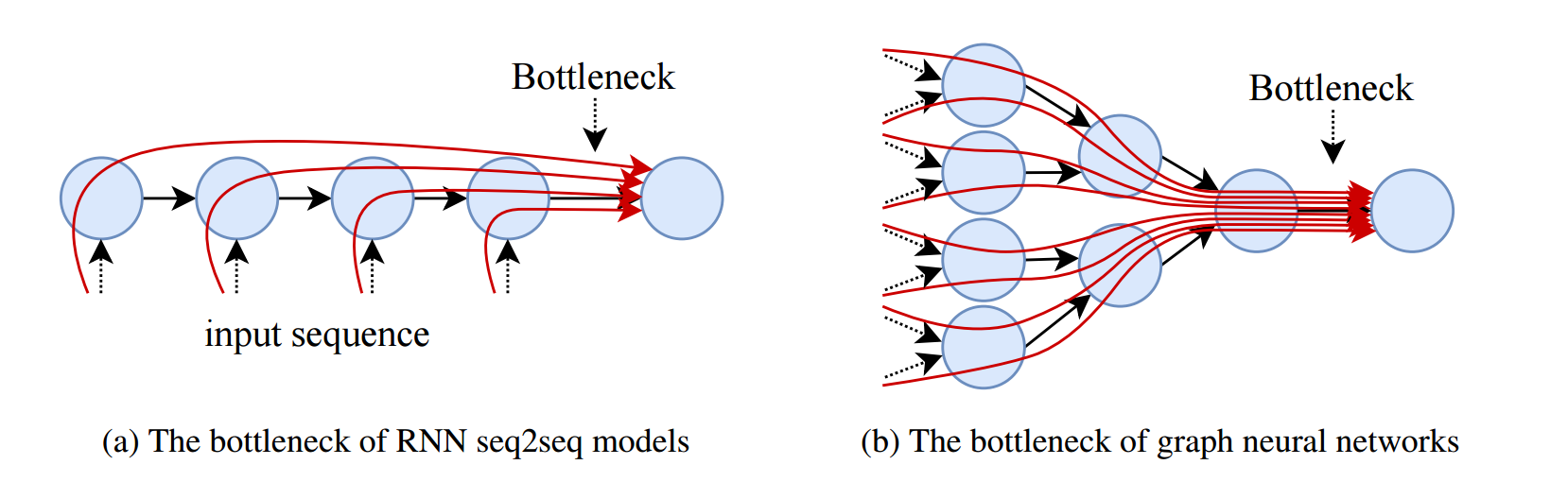
符号说明
- \(\mathcal{G} = (\mathcal{V}, \mathcal{E})\);
- \(\mathcal{N}_v\), 一阶邻居;
本文内容
-
GNN 大体可以表示为:
\[h_v^{(k)} = f_k(h_v^{(k-1)}, \{h_u^{(k-1)}|u \in \mathcal{N}_v; \theta_k\}), \]故没经过一层, 结点 \(v\) 就可以多接触到更远一阶的邻居;
-
虽然感受野的增长是线性的, 感受野内结点的数量却是 \(\mathcal{O}(\exp(K))\) 指数级别的, 这导致最开始图中出现的 over-squashing 的情况, 我们很难从众多的结点中分离剖析出我们所要的 long-range 的信息;
-
作者首先在 TREE-NEIGHBORSMATCH 数据集上进行实验, 该数据的某些 target 的 label 必须通过 r 阶邻居的信息来判断, 下面是不同方法的一个表现:
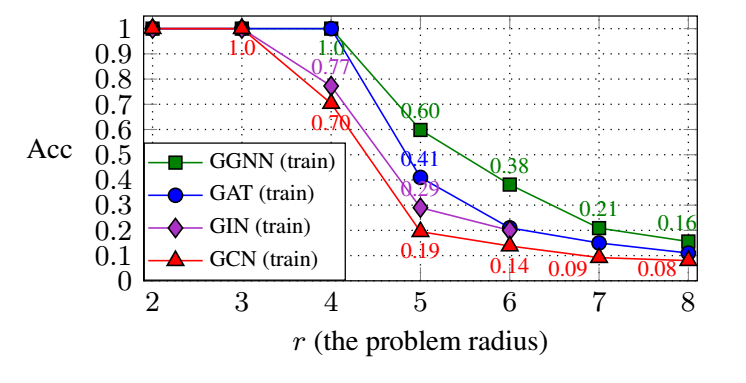
可以发现, over-squashing 从 r=4 开始就影响 GNN 的性能了, GAT 相比 GCN, GIN 因为它具备 weight 不同向量的能力, 所以勉强能够抓住一些 long-range 的信息;
- 接下来, 为了进一步证明 over-squashing 现象的存在, 作者设计了一个 fully-adjacent layer (FA), 它会被加在每个模型的最后一层, 在这最后一层里, 所有的结点都被认为是相连的, 即 \(\mathcal{N}(v) = \mathcal{V}\), 此时每个结点都能直接接触到所有的其它结点, 效果如下:

如上表所示, 提升非常大. 而且这种提升不是平凡的, 作者发现即使将所有的维度翻倍, 也仅有 5% 的提升而已.
代码
[official]

