Embedding Temporal Network via Neighborhood Formation
概
我不确定这篇文章好不好, 我只是对那些能结合随机过程, 微分方程的论文肃然起敬.
注: 这篇文章的作者都是经济管理的, 而 Hawkes process 在经济里头似乎还挺常见.
本文的思路
- 作者认为, 结点和结点之间交互的变化体现在图的变化之中, 如:
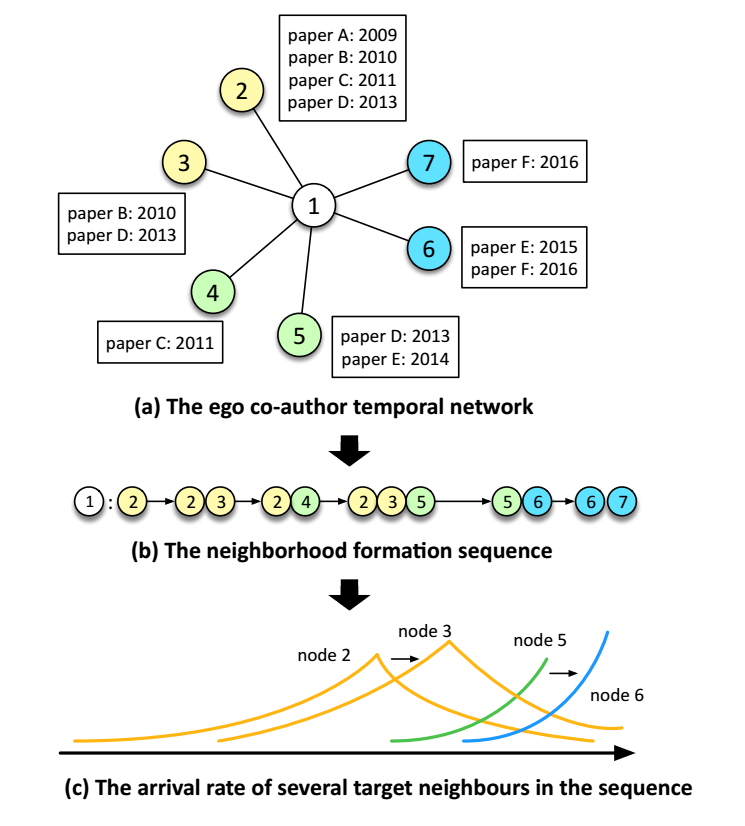
我们可以通过观察与 1 的合作者的论文变化情况推断出 1 的研究兴趣等等的变化;
-
为了建模这份关系, 作者引入 Hawkes Process,
\[\tilde{\lambda}_{y|x}(t) = \mu_{x, y} + \sum_{t_h < t} \alpha_{h, y} \kappa (t - t_h) \]描述了 \(y\) 出现在 \(x\) 的一个序列中的密度函数. 它和
1. \(\mu_(x, t)\), base rate 有关, 它定义为
$$
-|\bm{e}_x - \bm{e}_y |^2,
$$
即我们认为如果 \(x, y\) 的 embeddings 很相近, 则 \(y\) 出现在 \(x\) 的事件序列中的概率就会高;
2. \(\alpha_{h, y}\), 和上方同样的定义, 它描述了 \(y\) 和 已经出现在 \(x\) 中的事件的一个相似性, 类似的, 我们认为如果序列中出现了很多和 \(y\) 相近的点, 则 \(y\) 出现的概率也相应地会提高;
3. \(\kappa(t - t_h)\) 这是一个时间的衰减函数, 即我们认为越近的影响越重要; -
然后我们借此可以定义条件概率:
\[p(y|x, \mathcal{H}_x(t)) = \frac{\lambda_{y|x}(t)}{\sum_{y'} \lambda_{y'|x}(t)}, \: \lambda_{y|x}(t) = \exp(\tilde{\lambda}_{y|x}(t)), \]实际上是一个 softmax, \(\mathcal{H}_x(t)\) 是 \(t\) 时刻前和 \(x\) 有关的一个序列;
-
于是我们可以通过 ML 来优化 embeddings:
\[\max_{\bm{e}} \quad \log \mathcal{L} = \sum_{x \in \mathcal{V}} \sum_{y \in \mathcal{H}_x} \log p(y|x, \mathcal{H}_x(t)). \]
Q: 好像可以用在任意的序列问题上啊, 没必要非得是图啊.


