Dynamic Network Embedding by Modeling Triadic Closure Process
概
动态图的 embedding 学习, 本文引入 triad (三元组) 的概念, 希望所学习到的 embeddings 能够模拟动态图中的 triad closure process.
符号说明
- \(V = \{v_1, \ldots, v_M\}\), nodes;
- \(E = \{e_{ij}\}\), edges;
- \(W\), edge weigt;
- \(G^t = (V, E^t, W^t), t=1,\ldots, T\);
- \((v_i, v_j, v_k)\), triad, 其中 \((v_k, v_i), (v_k, v_j) \in E\), 但是 \((v_i, v_j)\) 不一定属于 \(E\), 若 \((v_i, v_j) \in E\), 称其为 close triad, 否则为 open triad.
Motivation
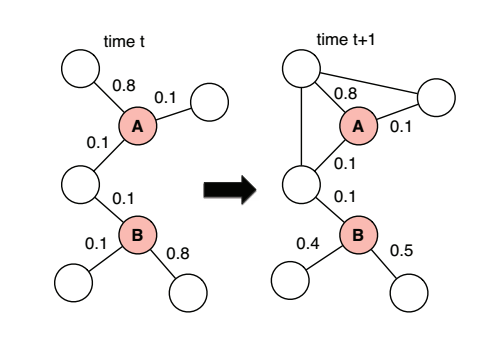
- 如图所示, \(A, B\) 的结构在 \(t\) 时刻是一致的 (邻居以及其上的边的权重都一样), 但是 A 可能是一个希望把朋友介绍给另外一个朋友, 这导致后续这些朋友间互相成为了朋友, 即从 open triad 变成了 close triad, 但是 B 可能是一个比较淡泊的人, 他的朋友间可能就不会因为他产生额外的联系;
- 作者希望学习特征 \(\bm{u}_i^t := f^t(v_i)\), 且这些特征能够保持上述的 triad closure process.
本文方法
-
首先, 作者定义在某个时刻 \(t\), \(v_k\) 到两个结点 \(v_i, v_j\) 的'距离':
\[\bm{x}_{ijk}^t = w_{ik}^t \cdot (\bm{u}_k^t - \bm{u}_i^t) + w_{jk}^t \cdot (\bm{u}_k^t - \bm{u}_j^t), \]其中 \(w_{ik}^t\) 表示 \(v_i, v_k\) 在 \(t\) 时刻的一个强度;
-
引入一个参数 \(\bm{\theta}\), 定义 \(v_i, v_j\) 在 \(v_k\) 的影响下产生联系的概率为:
\[P_{tr}^t (i, j, k) = \frac{1}{1 + \exp(-\langle \bm{\theta}, \bm{x}_{ijk}^t \rangle)}; \] -
假设 \(B^{t}(i, j)\) 为 \(v_i, v_j\) 的共同邻居的集合, 则下一时刻 \(v_i, v_j\) 发生联系的概率就可以建模为:
\[P_{tr_+}^t(i, j) = \sum_{\bm{\alpha}^{t, i, j} \not = \bm{0}} \prod_{k \in B^t(i, j)} (P_{tr}^t(i, j, k))^{\alpha_k^{t, i, j}} (1 - P_{tr}^t(i, j, k))^{1 - \alpha_k^{t, i, j}}, \]这里 \(\bm{\alpha}^{t, i, j}\) 是某个 \(B^t(i, j)\) 操作的组合, \(\alpha_k^{(t, i, j)} = 1\) 表示 \(v_k\) 为下一时刻 \((v_i, v_j)\) 产生联系做出了努力, 类似地, 定义
\[P_{tr_-}^t(i, j) = \prod_{k \in B^t(i, j)} (1 - P_{tr}^t(i, j, k)); \] -
于是, 我们可以定义
\[S_+^t = \{(i, j)| e_{ij} \not \in E^t \wedge e_{ij} \in E^{t+1}\} \\ S_-^t = \{(i, j)| e_{ij} \not \in E^t \wedge e_{ij} \not \in E^{t+1}\} \\ \]并定义如下损失
\[L_{tr}^t = -\sum_{(i, j) \in S_+^t} \log P_{tr_+}^t(i, j) -\sum_{(i, j) \in S_-^t} \log P_{tr_-}^t(i, j); \] -
此外, 作者定义两个 embedding 的距离为
\[g^{t}(j, k) = \|\bm{u}_j^t - \bm{u}_k^t\|_2^2, \]并通过如下损失来迫使邻居间的特征互相靠近:
\[L_{sh}^t = \sum_{(j, k) \in E^t, (j', k') \not \in E^t} w_{jk} \cdot \text{ReLU}(g^t(j, k) - g^t(j', k') + \xi); \] -
最后作者还认为不同时刻的 embeddings 的差异应当是比较小的, 所以同时最小化如下损失:
\[L_{smooth}^t = \left \{ \begin{array}{ll} \sum_{i=1}^N \|\bm{u}_i^t- \bm{u}_i^{t-1}\|_2^2 & t > 1 \\ 0 & t = 1; \end{array} \right . \] -
最后的目标函数是:
\[\text{argmin}_{\{\bm{u}_i^t, \bm{\theta}\}} \: \sum_{t=1}^T \Big [L_{sh}^t + \beta_0 L_{tr}^t + \beta_1 L_{smooth}^t \Big ]. \]
注: 文中用于逼近这个损失函数的策略这里就不提了.
代码
[official]


