node2vec: Scalable Feature Learning for Networks

目录

• 概
• 符号说明
• 本文方法
  • 采样策略
• 代码

Grover A. and Leskovec J. node2vec: Scalable Feature Learning for Networks. In ACM International Conference on Knowledge Discovery and Data Mining (KDD), 2016.

概

算是 Word2Vec 在图数据类型上的一个尝试.

符号说明

• \(G = (V, E)\), 图;
• \(f: V \rightarrow \mathbb{R}^d\), embeddings;
• \(N_S(u) \subset V\), 由采样策略 \(S\) 所采样得到的 \(u\) 的邻居结点.

本文方法

• 和 word2vec 一样, 我们希望为图的每个结点 \(u\) 赋予有意义的 embedding \(f(u)\);
• 假设我们通过采样策略 \(S\) 采样了一批邻居结点 \(N_s(u)\), 则模仿 word2vec 的 Skip-gram 方式, 通过如下方式学习 embeddings:
  \[\max_f \quad \sum_{v \in V} \log Pr(N_s(U)|f(u)); \]
  其中 (假设条件独立)
  \[Pr(N_s(U)|f(u)) \approx \prod_{n_i \in N_S(u)} Pr(n_i|f(u)), \]
  且
  \[\tag{1} Pr(n_i|f(u)) = \frac{\exp(f(n_i) \cdot f(u))}{\sum_{v \in V} \exp(f(v) \cdot f(u))}. \]
  对于 (1) 式, 通过负样本采样估计.

采样策略

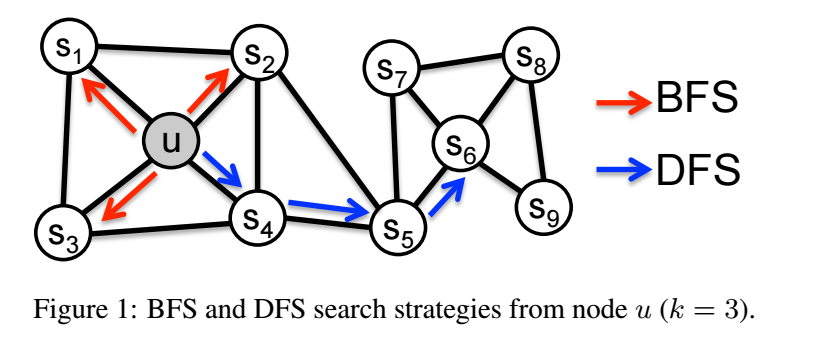
• 如上图所示, BFS 和 DFS 反映了两种不同的采样思路:

  1. BFS 能够更好地反映 homophily 假设, 即相近的相似;
  2. DFS 能够更好地反映 structural equivalence 假设, 即结构相近的点相似 (比如 \(u, s_6\), 二者虽然相隔很远, 但是周围的结构是很相似的);

• 作者认为这两种方法都太过于极端, 故采用如下的采样方式:

  \[p(c_i=x|c_{i-1} = v) = \left \{ \begin{array}{ll} \frac{\pi_{vx}}{Z} & \text{ if } (v, x) \in E \\ 0 & \text{ otherwise}. \end{array} \right . \]

  其中 \(\pi_{vx}\) 是这么定义的, 假设 \(c_{i-2} = t\), \((v, x)\) 的边上的权重为 \(w_{vx}\), 则

  \[\pi_{vx} = \alpha_{pq}(t, x) \cdot w_{vx}, \]

  其中

  \[\alpha_{pq}(t, x) = \left \{ \begin{array}{ll} \frac{1}{p} & \text{ if } d_{tx} = 0 \\ 1 & \text{ if } d_{tx} = 1 \\ \frac{1}{q} & \text{ if } d_{tx} = 2, \\ \end{array} \right . \]

  这里 \(d_{tx}\) 表示 \((t, x)\) 间的最短路径, 显然因为有 \(t \rightarrow v \rightarrow x\), 故

  \[d_{tx} \le 2. \]

• 注意到:

  1. 当 \(p\) 取一个小的值, 此时很容易会出现 \(t \rightarrow v \rightarrow t\) 的情况, 这个时候就是偏向于 BFS 了;
  2. 类似地, 当 \(q\) 比较大的时候, \(t \rightarrow v \rightarrow x \not = t\) 将很少发生, 此时也会导致采样偏向 BFS.

代码

[official]

[PyTorch]