How Powerful are Graph Neural Networks?
概
本文:
- 分析了现有 GNN 架构的表达能力的限制, 上限为 WL-Test;
- 提出了一些设计准则使得能够有和 WL-Test 一样的表达能力, 由此设计了 GIN (Graph Isomorphism Network).
注: 这里的表达能力是指网络判断两个图是否 同构 的能力.
符号说明
- \(G = (V, E)\), 图;
- \(X_v, v \in V\), node features;
- \(\mathcal{N}(v)\), 一阶邻居结点;
- \(\{\!\!\{\cdot \}\!\!\}\), multiset, 一个比较直观的理解看成是 Python 中的字典 (key 为元素, value 为元素出现的个数), 两个 multiset 等价即为有共同的元素且元素的个数相同;
- 一般的 GNN 的结构可以归纳为:\[\tag{(1)} a_v^{(k)} = \text{AGGREGATE}^{(k)} (\{h_u^{(k-1)}: u \in \mathcal{N}(v)\}) \\ h_v^{(k)} = \text{COMBINE}^{(k)}(h_v^{(k-1)}, a_v^{(k)}), \]\tag{2}
倘若, GNN 是用于 graph classification 的, 则最后的输出还对结点进行整合:\[h_G = \text{READOUT} (\{h_v^{(K)}: v \in G\}), \]并最终用于分类 (否则 \(h_v^{(K)}\) 即可用于 node 的分类了).
WL-Test
-
WL-Test 是用于判断两个图 \(G, G'\) 是否同构一个算法, 如果在算法进行过程中有一个阶段两个图的结点的标签不同, 则说明这两个图是非同构的, 但是需要注意的是, 即便到最后结点的标签均一致, 也不能断定 \(G, G'\) 同构.
-
WL-Test 的算法如下:
- 输入: \(G = (V, E)\), 结点的特征 \(X\);
- 初始化结点标签:\[\tag{3} l_v^{(0)} \leftarrow \text{hash}(X_v), \quad \forall v \in V. \]
- 重复如下步骤直到收敛:\[\tag{4} l_v^{(k)} \leftarrow \text{hash}( l_v^{(k-1)}, \{\!\!\{ l_w^{(k-1)}: w \in \mathcal{N}(v) \}\!\!\} ). \]
-
最后通过判断两个图收敛后的标签判断两个图是不是收敛.
-
需要注意的一点是, 如果两个图初始的特征 \(X\) 就不同那么他们就自然是不同构的, 所以在讨论两个图是否同构的时候一般默认二者具有相同的初始结点特征, 即相同的初始标签 \(l_v^{(0)}\). 在没有给定具体的结点的特征的时候, 即仅考虑图结构的时候, \(X\) 可以赋值为全 1.
-
一个重要的出发点: 可以发现, 除却一般不怎么讨论的初始化部分 (3), 决定 GNN 是否能够匹配 WL-Test 的表达能力的关键在于 (4). 对于 WL-Test, 若
\[ ( l_u^{(k-1)}, \{\!\!\{ l_w^{(k-1)}: w \in \mathcal{N}(u) \}\!\!\} ), \\ ( l_v^{(k-1)}, \{\!\!\{ l_w^{(k-1)}: w \in \mathcal{N}(v) \}\!\!\} ) \]不同, 则下一阶段的 \(l_u^{(k)}, l_v^{(k)}\) 就不会相同. 换言之, 这就要求 GNN 的每一层也要具有同样的性质, 这个性质其实就是函数里的 单射 (injective). 后续的讨论和改进实际上都是围绕这一点来的.
现阶段 GNN 的表达能力
-
(Lemma2) 按照 (1) (2) 所定义的 GNN 若能将两个图映射为两个不同的 embddings (即能区别开 \(G, G'\)), 则 WL-Test 算法能判断出 \(G, G'\) 是不同构的.
-
Lemma2 直接说明了, 按照 (1) (2) 的 GNN 的表达能力的上限是 WL-Test.
proof:
注意到, 决定 (2) 的输出的实际上取决于输入特征
故倘若 GNN 能判断出 WL-Test 不能判断出的非同构情况, 则存在一特例使得
但是
因为初始特征 \(h_u^{(0)} = h_v^{(0)}\), 所以我们可以通过归纳法证明. 可以假设 \(k-1\) 时成立结点的标签和特征均相等, 则通过 (2) 可以得到的
这就产生了矛盾. 所以 Lemma2 成立.
GIN
-
(Theorem3) 通过 (1) (2) 所定义的 GNN 能够判断出 WL-Test 所能判断出的所有非同构的情况, 若
- GNN 通过如下方式聚合和更新结点特征\[ h_v^{(k)} = \phi \big( h_v^{(k-1)}, f\big( \{\!\!\{ h_w^{(k-1)}: w \in \mathcal{N}(v) \}\!\!\} \big) \big), \]
其中 \(f, \phi\) 均为单射.
- 最后的 graph-level readout 也是单射.
- GNN 通过如下方式聚合和更新结点特征
这部分的证明其实通过最开始的 WL-Test 的分析就已经了然了. 具体的证明可以回看原文, 并不麻烦.
-
(Lemma5) 如果 \(\mathcal{X}\) 空间时可数的, 则存在一映射 \(f: \mathcal{X} \rightarrow \mathbb{R}^{n}\) 满足 \(h(X) = \sum_{x \in X} f(x)\) 对于每个有限大小的 multiset \(X \subset \mathcal{X}\) 都是唯一的. 此外, 任何 multiset function \(g\) 都可以通过某个 \(\phi\) 分解为 \(g(X) = \phi (\sum_{x \in X} f(x))\).
-
Lemma5 给了一种比较方便的 multiset 的处理形式, 这是 GIN 使用 sum aggregation 而不是 mean/max 的理论基础.
-
(Corollary 6) Corollary 6 证明了, 定理 3 中的单射 \(\phi\) 是存在的, 事实上存在 \(f\) 和无穷多的 \(\epsilon\) (包括所有无理数) 使得
\[h = (1 + \epsilon) \cdot f(c) + \sum_{x \in X} f(x) \]都是 \((c, X) \in \mathcal{X} \times \mathcal{X}\) 到 \(h\) 上的单射.
同样地, 任何 \(g(c, X)\) 都可以通过某个 \(\varphi\) 分解为\[g(c, X) = \varphi \bigg((1 + \epsilon) \cdot f(c) + \sum_{x \in X} f(x) \bigg). \]注意到,
\[f^{(k+1)}(h_v^{(k)}) = f^{(k+1)} \circ \varphi^{(k)} (\cdots), \]故我们可以用 MLP 来拟合 \(f^{(k+1)}\circ \varphi^{(k)}\), 于是可以记作
\[h_v^{(k)} = \text{MLP}^{(k)}((1 + \epsilon) \cdot h_v^{(k-1)} + \sum_{w \in X} h_w^{(k-1)}), \forall v \in V. \] -
注: \(\epsilon\) 可以是可学习的参数, 也可以是固定值 (如文中建议的 0).
-
最后的 GIN 作用于图的分类的结构如下:
\[h_G = \text{CONCAT(READOUT}(\{h_v^{k}|v \in G\}) | k = 0,1,2,\ldots, K ), \]\(\text{READOUT}\) 采用 summing.
其它的注意事项
-
MLP 作者后面时没有跟激活函数的, 因为作者证明实际上存在 multiset \(X_1 \not= X_2\), 但
\[ \sum_{x \in X_1} \text{ReLU}(Wx) = \sum_{x \in X_2} \text{ReLU} (Wx), \]即单射的性质会丧失 (当然这个和 ReLU 的性质有关系, 换成其它的单射可能就不会有这个问题了)
-
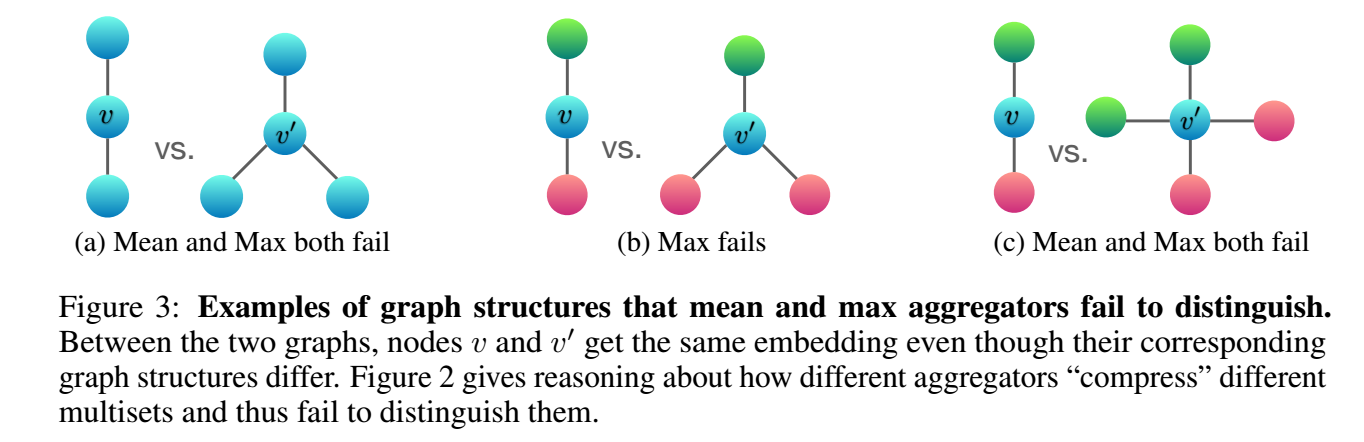
Mean/Max 为什么不行, 因为它们实际上也会导致单射的性质丢失. 我们注意到
\[\text{Mean} \bigg( \bigg\{ x_1: c_1, x_2: c_2, \ldots, x_n:c_n \bigg\} \bigg) = \text{Mean} \bigg( \bigg\{ x_1: k \cdot c_1, x_2: k\cdot c_2, \ldots, x_n: k \cdot c_n \bigg\} \bigg) \]对于任意的 \(k=1,2,\ldots\) 成立 (这里我用 python 字典的方式表述 multiset). 所以 Mean 实际上考虑的是 multiset 的分布. 而 Max 实际上更加极端
\[\text{Mean} \bigg( \bigg\{ x_1: c_1, x_2: c_2, \ldots, x_n:c_n \bigg\} \bigg) = \text{Mean} \bigg( \bigg\{ x_1: 1, x_2: 1, \ldots, x_n: 1 \bigg\} \bigg), \]直接就相当于 multiset 退化为一般的 set 了. 丢失的信息会更加严重. 不过在实际中, 由于特征往往是不同的, 所以 multiset 往往就是 set, 所以 mean/max 在实际中的效果也不会太差.
实际的操作
- 为了仅仅提取和图结构相关的特征, 作者在初始化结点特征的时候采用了两种方案:
- 所有的节点特征均为 1;
- 所有的结点的特征为 degree 的 one-hot encoding.
代码
[official]


