Weisfeiler-Lehman Test
概
本文介绍了 WL-Test 和它的一些变体, 它会和所设计的 GNN 的表达能力有关, 实际上由不同的变体会导出不同版本的 GNN, 所以还是很有意义的. 不过对于下面这些 Test 如何起到区分异构图的证明我并没有看过, 这里只是列出了算法.
符号说明
- \(G=(V, E, X_V)\), 图;
- \(V = \{1, 2, \ldots, n\} := [n]\), 结点;
- \(E \subset V \times V\), 边;
- \(X_V = \{X_v: v \in V\} \subset \mathbb{R}^d\), 点上的特征;
- \(\mathcal{N}_G(v) = \{w: (v, w) \in E\}\), 邻居结点;
注: 如果不存在结点特征, 可以赋予 \(X_v = 1, \forall v \in V\).
同构
称 \(G = (V, E, X_V), G' = (V', E', X_{V}')\) 同构, 若存在置换 (permutation) \(\prod\) 使得
$$
\prod V = V' \
\prod E = E': \prod (u, v) = (\prod u, \prod v) \
\prod X_V = X_{\prod V} = X_{V}'.
$$
multiset
multiset \(\{\!\{ \cdot \}\!\}\) 可以理解成如下的键值对:
$$
{c_v: \text{count}(c_v)},
$$
即其蕴含了 key 和该 key 出现的次数的信息.
WL
当 \(\text{WL}(G) \not = \text{WL}(G')\) 的时候, \(G, G'\) 不同构, 反之不一定.
1-WL
- 输入: \(G = (V, E, X_V)\);
-
赋予状态:
\[c_v^0 \leftarrow \text{hash}(X_v), \quad \forall v \in V; \] -
重复下列操作:
\[c_v^l \leftarrow \text{hash}(c_v^{l-1}, \{\!\{c_w^{l-1}: w \in \mathcal{N}_G(v) \}\!\}), \quad \forall v \in V \]直到满足
\[c_v^l = c_v^{l-1}, \quad \forall v \in V; \]
- 输出 \(\{\!\{ c_v^l: v \in V \}\!\}\).
k-WL
注: 这里的 \(k\) 不是单纯的 \(k\), 因为 k-WL with \(k=1\) 不是 1-WL, 1-WL 实际上等价于 k-WL with \(k=2\).
令
下面的算法是每次处理 \(k\) 个点的算法, 记
以及, 下面的 \(\text{hash}(G(\bm{v}))\) 满足:
当且仅当
- 输入: \(G = (V, E, X_V)\);
-
赋予状态:
\[c_{\bm{v}}^0 \leftarrow \text{hash}(G(\bm{v})), \quad \forall \bm{v} \in V^k; \] -
重复下列操作:
\[c_{\bm{v},i}^l \leftarrow \{\!\{c_w^{l-1}: w \in \mathcal{N}_i(\bm{v}) \}\!\}, \quad \forall \bm{v} \in V^k, i \in [k] \\ c_{\bm{v}}^l \leftarrow \text{hash}(c_{\bm{v}}^{l-1}, c_{\bm{v}, 1}^{l}, \ldots, c_{\bm{v}, k}^{l}), \quad \forall \bm{v} \in V^k, \]直到满足
\[c_{\bm{v}}^l = c_{\bm{v}}^{l-1}, \quad \forall \bm{v} \in V^k; \]
- 输出 \(\{\!\{ c_{\bm{v}}^l: \bm{v} \in V \}\!\}\).
k-FWL
下面, 我们用 \(c_{\bm{v}[i] \leftarrow w}\) 来表示
- 输入: \(G = (V, E, X_V)\);
-
赋予状态:
\[c_{\bm{v}}^0 \leftarrow \text{hash}(G(\bm{v})), \quad \forall \bm{v} \in V^k; \] -
重复下列操作:
\[c_{\bm{v},w}^l \leftarrow (c_{\bm{v}[1] \leftarrow w}^{l-1}, \ldots, c_{\bm{v}[k] \leftarrow w}^{l-1}), \quad \forall \bm{v} \in V^k, w\in V \\ c_{\bm{v}}^l \leftarrow \text{hash} (c_{\bm{v}}^{l-1}, \{\!\{c_{\bm{v},w}^{l}: w \in V \}\!\}, \quad \forall \bm{v} \in V^k \\ \]直到满足
\[c_{\bm{v}}^l = c_{\bm{v}}^{l-1}, \quad \forall \bm{v} \in V^k; \]
- 输出 \(\{\!\{ c_{\bm{v}}^l: \bm{v} \in V \}\!\}\).
例子
考虑如下的两个不同构的图 \(G, H\) (假设 features 是相同的):
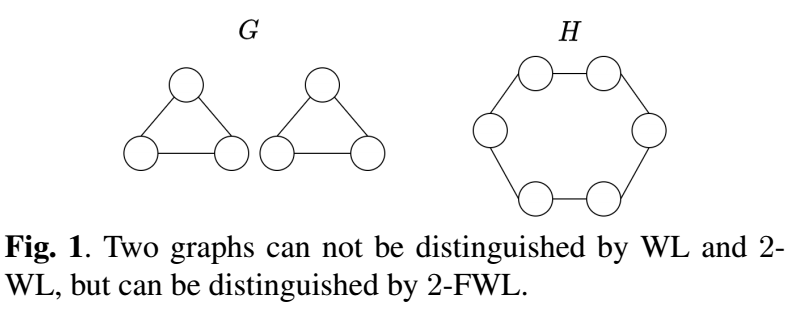
注: 标注就是左边 (1, 2, 3), 右边 (4, 5, 6).
2-WL:
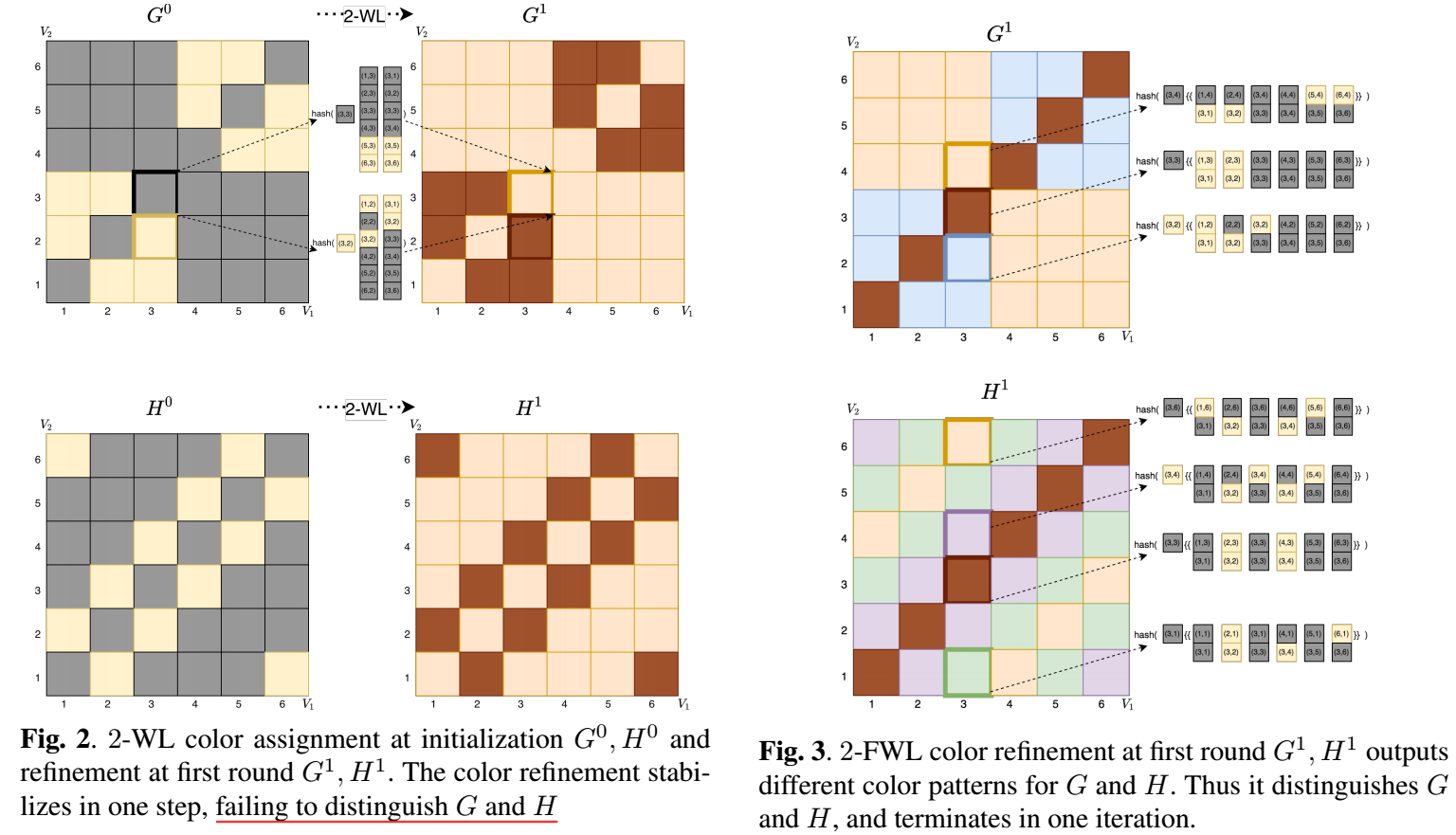
- 初始化, 因为结构是相同的, 所以起初会分成两组 (\((v_i, v_j) \in E\) 或 \((v_i, v_j) \not \in E\)), 故可以按照图 2 中的 \(G^0, H^0\) 进行颜色的划分 (均为 12 yellows, 24 greys);
- 注意到此时 \(\mathcal{N}_1(\bm{v}), \mathcal{N}_2 (\bm{v})\) 实际上是 \(\bm{v}\) 对应位置的列和行, 以 (3, 3) 位置为例 (图中的颜色标注有误),\[\mathcal{N}_{1}((3, 3)) = \{(i, 3): i \in [6]\}, \\ \mathcal{N}_{2}((3, 3)) = \{(3, j): j \in [6]\}, \\ \]
- 故\[c_{(3, 3), 1}^1 = c_{(3, 3), 2}^1 = \{\!\{4 \text{ greys }, 2 \text{ yellows } \}\!\}; \]
- 于是\[c_{(3, 3)}^1 = \text{hash}(c_{(3, 3)}^0, \{\!\{4 \text{ greys }, 2 \text{ yellows } \}\!\}); \]
- 进一步我们会发现, \(c_{\bm{v}}^1\) 可以表示成\[c_{\bm{v}, 1}^1 = c_{\bm{v}, 2}^1 = \{\!\{4 \text{ greys }, 2 \text{ yellows } \}\!\}, \\ \text{hash}(c_{\bm{v}}^0, \{\!\{4 \text{ greys }, 2 \text{ yellows } \}\!\}), \]故新的 hash 值实际上由初始值 \(c_{\bm{v}}^0\) 决定, 所以 \(G^1, G^0\) 的模式 实际上是一样的, 故到 \(G^1\) 就可以停止了;
- 对于 \(H\) 也是同理的, 可以发现, 在算法停止的时候, \(G^1, H^2\) 的颜色模式依旧是一致的, 故 2-WL 算法是没法区分这两个图的;
另一方面 2-FWL 它是能够得出 \(G, H\) 异构的结论的, 所以 2-FWL 的判断能力是强于 2-WL 的. 实际上, 作者在文中说, k-WL 是和 (k-1)-FWL 的判断能力是一致的, 后者会更加高效一点.


