Graph Attention Networks

目录

• 概
• 符号说明
• 框架
• 代码

Veli\check{c}kovi\acute{c} P., Cucurull G., Casanova A., Romero A. and Li\grace{o} P. and Bengio Y. Graph attention networks. In International Conference on Learning Representations (ICLR), 2018.

概

结合 attention 的图神经网络.

符号说明

• \(\mathcal{G} = (\mathcal{V}, \mathcal{E})\), 图;
• \(|\mathcal{V}| = N\);
• \(\mathcal{N}_i\), 结点 \(v_i \in \mathcal{V}\) 的一阶邻居结点;

框架

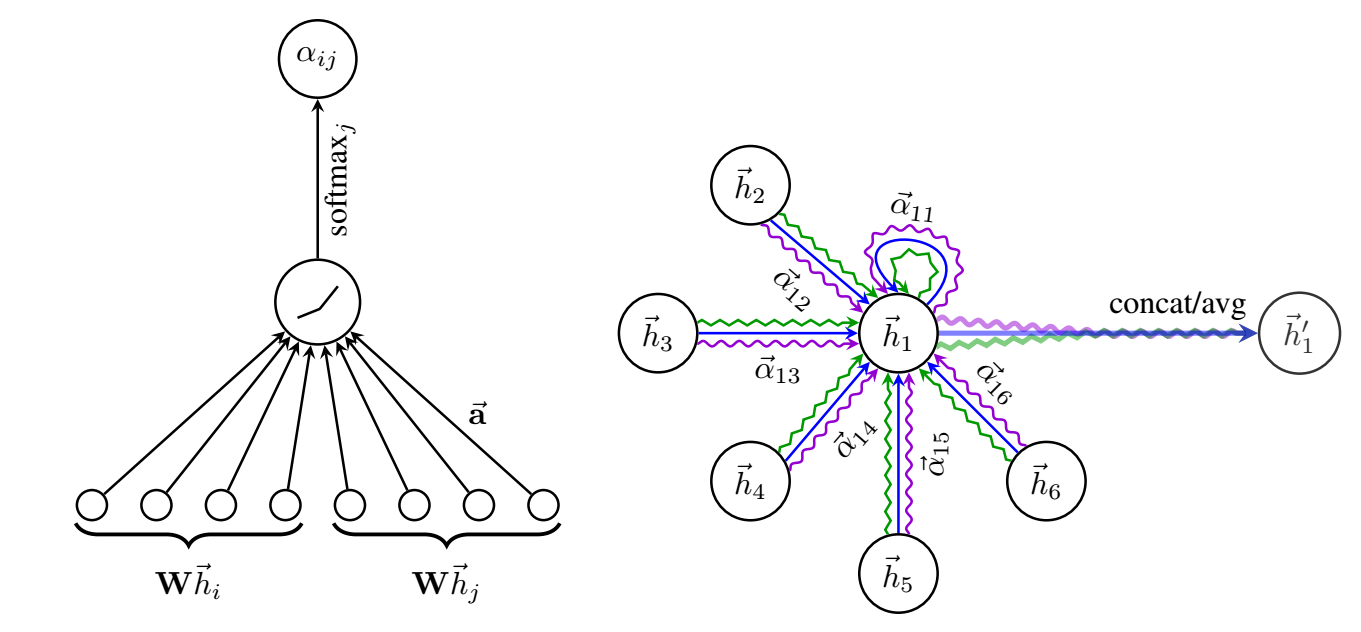
• 每一层进行如下操作:

  1. 输入起始特征 \(H = \{\bm{h}_1, \bm{h}_2, \ldots, \bm{h}_N\}, \bm{h}_i \in \mathbb{R}^F\);

  2. 通过共享参数 \(W^k, k=1,2,\ldots, K\) 得到:

     \[H^k = \{W^k\bm{h}_1, \ldots, W^k \bm{h}_N\}; \]

  3. 计算结点 \(j \rightarrow i\) 的 attention (通过聚合一阶邻居):

     \[\alpha_{ij}^k = \frac{\exp(\text{LeakyReLU}(\bm{w}^T [\bm{h}_i^k \| \bm{h}_j^k]))}{\sum_{v \in \mathcal{N}_i}\exp(\text{LeakyReLU}(\bm{w}^T [\bm{h}_i^k \| \bm{h}_v^k]))}, \]

     其中 \(\|\) 表示拼接操作;

  4. 得到新的特征:

     \[\bm{h}_i' = \|_{k=1}^K \sigma(\sum_{j \in \mathcal{N}_i} \alpha_{ij}^k \bm{h}_j^k) \]

• 需要注意的是, 最后一层采用的是 averaging:

  \[\bm{h}_i' = \sigma(\frac{1}{K}\sum_{k=1}^K \sum_{j \in \mathcal{N}_i} \alpha_{ij}^k \bm{h}_j^k) \]

代码

[official]