On Sampled Metrics for Item Recommendation
Krichene W. and Rendle S. On sampled metrics for item recommendation. KDD, 2020.
概
作者对推荐系统中 sampled-based ranking 的评估进行了批判.
符号说明
- \(\mathbf{x} \in \mathcal{D}\), instance (user, query ...);
- \(\mathcal{I}\), item set, \(|\mathcal{I}| = n\);
- \(\mathscr{A}\), 推荐算法;
- \(\mathbf{y} = \{y_1, y_2, \ldots, y_l\} \subset \mathcal{I}\), instance \(\mathbf{x}\) 所感兴趣的 items;
- \(\mathcal{R}(\mathscr{A}, \mathbf{x})\), 给定 instance \(\mathbf{x}\) 和推荐算法 \(\mathscr{A}\), 返回 \(\mathscr{A}\) 对 \(\mathbf{x}\) 所感兴趣的 \(\mathbf{y}\) 排序结果. 比如, \(\mathbf{x}\) 对 \(y_1, y_2\) 感兴趣, 若 \(\mathcal{R}(\mathscr{A}, \mathbf{x}) = \{3, 5\}\) 则表示 \(\mathscr{A}\) 认为 \(y_1, y_2\) 在所有的 items 中的排名为 3 和 5 (排名从 1 开始, 越靠前说明算法认为这个 item 越适合 \(\mathbf{x}\)).
- 注意: 在没有起义的情况下, 我们省略 \(\mathscr{A}, \mathbf{x}\), 仅用 \(\mathcal{R}\) 表示 \(\mathcal{R}(\mathscr{A}, \mathbf{x})\).
- \(\mathscr{M}(\mathcal{R})\) 表示衡量排序结果 \(\mathcal{R}\) 的一个指标.
- \([n] = \{1, 2, \ldots, n\}\).
Metrics
-
给定 Metric \(\mathscr{M}\), 其在整个数据上的指标通常采用如下的方式测量:
\[ \frac{1}{|\mathcal{D}|} \sum_{\mathbf{x} \in \mathcal{D}} \mathscr{M}(\mathcal{R}(\mathscr{A}, \mathbf{x})). \] -
接下来, 我们介绍推荐系统中一些常见的 \(\mathscr{M}\).
-
AUC:
\[\text{AUC}(\mathcal{R}; n) = \frac{1}{|\mathcal{R}|} \sum_{r \in \mathcal{R}} \frac{\sum_{r' \in [n] \setminus \mathcal{R}} \delta(r < r')}{n - |\mathcal{R}|}, \]如果 \(|\mathcal{R}| = 1\), 则有
\[\text{AUC}(\mathcal{R}; n) = \frac{n - r}{n - 1}. \] -
Precision:
\[\text{Prec}(\mathcal{R}; k) = \sum_{r \in \mathcal{R}} \frac{\delta(r \le k)}{k}. \]如果 \(|\mathcal{R}| = 1\),
\[\text{Prec}(\mathcal{R}; k) = \frac{\delta(r \le k)}{k}. \] -
Recall:
\[\text{Recall}(\mathcal{R}; k) = \sum_{r \in \mathcal{R}} \frac{\delta(r \le k)}{|\mathcal{R}|}. \]如果 \(|\mathcal{R}| = 1\),
\[\text{Recall}(\mathcal{R}; k) = \frac{\delta(r \le k)}{1}. \] -
Average Precision:
\[\text{AP}(\mathcal{R}; k) = \frac{1}{\min(|\mathcal{R}|, k)} \sum_{i=1}^k \delta(i \in \mathcal{R}) \text{Prec}(\mathcal{R}; i). \]如果 \(|\mathcal{R}| = 1\),
\[\text{AP}(\mathcal{R}; k) = \frac{\delta(r \le k)}{r}. \] -
Normalized discounted cumulative gain:
\[\text{NDCG}(\mathcal{R}; k) = \frac{1}{\sum_{i=1}^{\min(|\mathcal{R}|, k)} \frac{1}{\log_2 (i + 1)}} \sum_{i=1}^k \frac{\delta (i \in \mathcal{R})}{\log_2 (i + 1)}. \]如果 \(|\mathcal{R}| = 1\),
\[\text{NDCG}(\mathcal{R}; k) = \frac{\delta(r \le k)}{\log_2 (r + 1)}. \]
Sampled-based ranking
-
上面的指标都是 full-ranking, 即排序是在整个 item 集合 \(\mathcal{I}\) 之上的.
-
但是, 如果 \(|\mathcal{I}| = n\) 很大, 那么每次排序可能都需要很长的时间. 所以, 一种常用的 sampled-based ranking 是对于每个正样本 \(y\), 采样 \(m\) 个负样本 \(i_1, i_2, \ldots, i_m \not \in \mathbf{y}\).
-
然后 \(y\) 在 \(\{y, i_1, i_2, \ldots, i_m\}\) 中的排名用于后续的评估.
例子
-
让我们看一个例子:
-
上图展示了三个不同的推荐系统 \(A, B, C\) 给五个实例的预测排名, 然后后面是精确的评估. 从其上的表现也可以发现:
- AUC 是一个很 mean 的指标, 它要求推荐系统一视同仁;
- AP, NDCG 比较在意排名靠前的结果.
- Recall@10 对排名 10 之前的一视同仁, 但是之后的就会有极大的惩罚.
-
实际上, 这些指标对于不同的 \(r\) 的评估结果如下 (\(|\mathcal{R}| = 1\)).
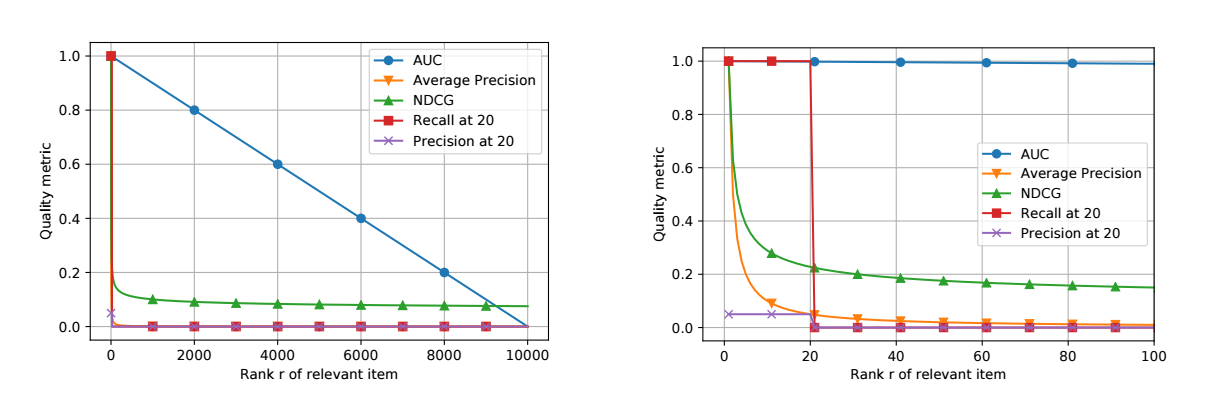
- 那, 如果我们按照 sampled-based ranking 评估会是怎么样的一个结果呢?
- 可以发现, 推荐系统 A 始终取得了一个最好的结果, 这说明:
- Sampled-based ranking 可能是不保序的, 即当 full-ranking 下 C 比 A 好的时候, 在 Sampled-based ranking 下可能会得出结果 A 比 C 好.
- Sampled-based ranking 下的不同指标, 如 AP, NDCG 等, 会变得 mean, 和 AUC 有着类似的倾向.
Sampled metrics
-
假设 \(|\mathcal{R}| = 1\), 令 \(\tilde{\mathcal{R}}\) 表示 Sampled-based ranking 下的排名. 一个很自然的愿景是保序性:
\[\frac{1}{|\mathcal{D}|} \sum_{\mathbf{x} \in \mathcal{D}} \mathscr{M}(\mathcal{R}(\mathscr{A}, \mathbf{x})) > \frac{1}{|\mathcal{D}|} \sum_{\mathbf{x} \in \mathcal{D}} \mathscr{M}(\mathcal{R}(\mathscr{B}, \mathbf{x})) \\ \Leftrightarrow \mathbb{E}\bigg[\frac{1}{|\mathcal{D}|} \sum_{\mathbf{x} \in \mathcal{D}} \mathscr{M}(\tilde{\mathcal{R}}(\mathscr{A}, \mathbf{x})) \bigg ] > \mathbb{E}\bigg[ \frac{1}{|\mathcal{D}|} \sum_{\mathbf{x} \in \mathcal{D}} \mathscr{M}(\mathcal{\tilde{R}}(\mathscr{B}, \mathbf{x})) \bigg]. \] -
当然, 根据上面的分析, 我们已经发现这个性质是不成立的, 这里我们进一步看看到底是为什么. 为此, 我们需要计算 (注意, 我们假设 \(|\mathcal{R}| = 1\))
\[\mathbb{E}[\mathscr{M}(\mathcal{\tilde{R}})]= \mathbb{E}[\mathscr{M}(\tilde{r})] = \sum_{i=1}^{m+1} p(\tilde{r} = i) \mathscr{M}(i). \] -
\(p(\tilde{r}=i)\) 是 target \(y\) 在样本 \(\{y, i_1, \ldots, i_m\}\) 中的排名为 \(i\) 的概率. 由于 \(i_k\) 是均匀采样的, 故
\[p(j < r) = \frac{r-1}{n - 1} = 1 - \text{AUC}(r; n). \] -
故, \(\tilde{r}\) 实际上等价于从如下分布中采样:
\[\tilde{r} \sim B(m, \frac{r-1}{n-1}) + 1, \]其中 \(B(m, \frac{r-1}{n-1}\) 表示成功概率为 \(\frac{r-1}{n-1}\) 的二项分布.
-
故
\[p(\tilde{r} = i) = \left ( \begin{array}{c} m \\ i-1 \end{array} \right ) (\frac{r-1}{n-1})^{i-1} (\frac{n-r}{n-1})^{m-i+1}. \] -
此外, 我们有
\[\mathbb{E}[\tilde{r}] = m \frac{r-1}{n-1} + 1 \] -
接下来我们讨论不同的 matric 的期望.
-
AUC:
\[\begin{array}{ll} \mathbb{E}_{\tilde{r}} [\text{AUC}(\tilde{r}; m + 1)] &=\mathbb{E}_{\tilde{r}} [\frac{m + 1 - \tilde{r}}{m}] \\ &=\frac{m + 1 - \mathbb{E}_{\tilde{r}}[\tilde{r}]}{m} \\ &=\frac{m - m \frac{r-1}{n-1}}{m} \\ &=\frac{n-r}{n-1}. \end{array} \]故 Sampled-based ranking 下, AUC 是无偏的.
-
Precision:
\[\begin{array}{ll} \mathbb{E}_{\tilde{r}}[\text{Prec}(\mathcal{\tilde{r}}; k)] &=\mathbb{E}_{\tilde{r}}[\delta(\tilde{r} \le k) \frac{1}{k}] \\ &=\sum_{i=1}^{m+1} p(\tilde{r}=i) \delta(i \le k) \frac{1}{k} \\ &=\sum_{i=1}^{k} p(\tilde{r}=i) \frac{1}{k} \\ &=\frac{1}{k} F(k-1; m, \frac{r-1}{n-1}), \end{array} \]这里 \(F(k) := \mathbb{P}(\tilde{r} \le k)\) 表示二项分布的分布函数.
-
Recall:
\[\begin{array}{ll} \mathbb{E}_{\tilde{r}}[\text{Recall}(\mathcal{\tilde{r}}; k)] &=\mathbb{E}_{\tilde{r}}[\delta(\tilde{r} \le k) ] \\ &=\sum_{i=1}^{m+1} p(\tilde{r}=i) \delta(i \le k) \\ &=\sum_{i=1}^{k} p(\tilde{r}=i) \\ &= F(k-1; m, \frac{r-1}{n-1}), \end{array} \] -
AP:
\[\begin{array}{ll} \mathbb{E}_{\tilde{r}}[\text{AP}(\mathcal{\tilde{r}}; k)] &=\mathbb{E}_{\tilde{r}}[\delta(\tilde{r} \le k) / \tilde{r}] \\ &=\sum_{i=1}^{m+1} \frac{1}{i} p(\tilde{r}=i) \delta(i \le k) \\ &=\sum_{i=1}^{k} p(\tilde{r}=i) \cdot \frac{1}{i}. \end{array} \]当 \(k = m + 1\), 且 \(r > 1\) 的时候, 我们有
\[\begin{array}{ll} \mathbb{E}_{\tilde{r}}[\text{AP}(\mathcal{\tilde{r}}; m+1)] &=\mathbb{E}_{\tilde{r}} [\frac{1}{\tilde{r}}] \\ &=\mathbb{E}_{\tilde{r}- 1} [\frac{1}{\tilde{r} - 1}] \\ &=\frac{1 - (1 - p(j < r))^{m+1}}{p(j < r) (m + 1)} \\ &=\frac{1 - (\frac{n-r}{n-1})^{m+1}}{(r - 1) \frac{m + 1}{n - 1}} \\ &=\frac{1 - \text{AUC}(r; n)^{m + 1}}{(r - 1) \frac{m + 1}{n - 1}}. \end{array} \]这里, 我们用到了二项式分布的性质, 对于二项式分布 \(k \sim B(m; p)\), \(\mathbb{E}[1/(k + 1)]\) 为
\[ \mathbb{E}[\frac{1}{k + 1}] = \frac{1 - (1 - p)^{m + 1}}{p (m + 1)}. \] -
非常有意思的是, 可以观测到:
- 当 \(\text{AUC}(r; n) \approx 0\) 的时候, 即推荐模型很差的时候, \(\text{AP}(\tilde{r}; m+1)\) 和 和 \(\text{AP}(r; m+1)\) 给出的结果是一致的;
- 当 \(\text{AUC}(r; n) \approx 1\) 的时候, 显然我们需要采样很多的负样本, 即 \(m\) 比较大的情况下, 效果才能比较一致.
