Addressing Unmeasured Confounder for Recommendation with Sensitivity Analysis
概
以往的鲁棒的 estimator 在存在 unmeasured confounder 的时候会导致 counfounding bias, 本文通过给定 bound 下的对抗训练来解决这一问题.
符号说明
- \(\mathcal{U}\), users;
- \(\mathcal{I}\), items;
- \(\mathcal{D} = \mathcal{U} \times \mathcal{I}\), user-item pairs;
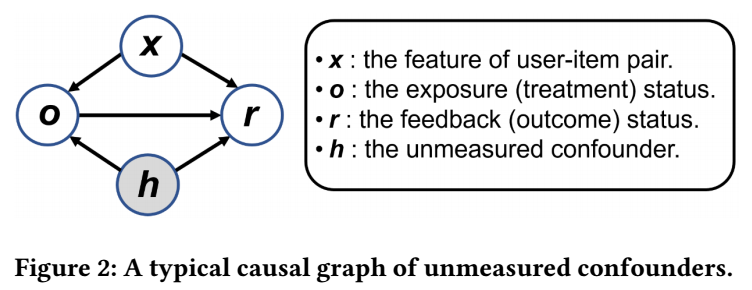
- \(x_{u,i}\), user-item feature;
- \(o_{u,i} \in \{0, 1\}\), 1 表示 \(i\) 曝光给 \(u\);
- \(r_{u, i}\), rating;
- \(\mathcal{O} = \{(u, i)| (u, i) \in \mathcal{D}, o_{u, i} = 1\}\);
问题
-
假设 \(o, x, y, h\) 满足上面的因果图, 其中 \(h\) 是一些无法观测的变量;
-
设想, 我们希望通过一个模型 \(f_{\phi}(\cdot)\) 来估计 \(r\). 我们模拟的是这样的一个流程:
- 将 item \(i\) 曝光给 user \(u\), 即 \(do(o_{u,i} = 1)\);
- 获得一个指标 \(r_{u,i}(1) := r_{u,i}| do(o_{u,i} = 1\);
-
那么自然地, 我们希望 \(\hat{r}_{u,i}(1) = f_{\phi}(x_{u,i})\) 能够逼近真实地 \(r_{u,i}(1)\):
\[\min_{\phi} \quad \mathcal{L}_{ideal}(\phi) = \frac{1}{|\mathcal{D}|} \sum_{(u, i) \in \mathcal{D}} e_{u, i}, \]其中
\[e_{u, i} := (\hat{r}_{u, i}(1) - r_{u, i}(1))^2; \] -
但是, 由于只有部分 \(\mathcal{O}\) 曝光, 故实际上我们只能优化:
\[\mathcal{L}_{real}(\phi) = \frac{1}{|\mathcal{O}|} \sum_{(u, i) \in \mathcal{O}} e_{u, i}; \] -
倘若, 我们能够知道确切的 propensity score:
\[\tilde{p}_{u, i} = \mathbb{P}(o_{u,i} = 1| x_{u, i}, h_{u,i}), \]则可以通过
\[\mathcal{L}_{IPS}(\phi) = \frac{1}{|\mathcal{D}|} \sum_{(u, i) \in \mathcal{D}} \frac{o_{u,i} e_{u,i}}{\tilde{p}_{u,i}} \]来优化, 注意到该式关于 \(o\) 的期望:
\[\begin{array}{ll} \mathbb{E}[\mathcal{L}_{IPS}] &=\mathbb{E}_{x, h} \frac{\mathbb{E}_{o, r(1)} [o_{u,i} e_{u,i}] }{\tilde{p}_{u,i}} \\ &=\mathbb{E}_{x, h} \frac{\mathbb{E}_{o} [o_{u,i}] \mathbb{E}_{r(1)}[e_{u,i}] }{\tilde{p}_{u,i}} \leftarrow r(1) \perp \!\!\! \perp o | x, h \\ &=\mathbb{E}_{x, h} \frac{\tilde{p}_{u,i} \mathbb{E}_{r(1)}[e_{u,i}] }{\tilde{p}_{u,i}} \\ &=\mathbb{E}_{x, h, r(1)} [e_{u,i}] = \mathbb{E}[\mathcal{L}_{ideal}]. \end{array} \]故这说明该估计量是无偏的.
-
但是由于 \(h\) 是不可观测的, 故 \(\tilde{p}_{u, i}\) 也是难以估计的; 而之前的方法, 多半假设因果图中不存在无法观测的变量, 并用
\[\hat{p}_{u, i} = \mathbb{P}(o_{u,i} = 1| x_{u, i}), \]来替代 \(\tilde{p}_{u, i}\). 虽然颇有成效, 但在理论上, 该估计量是有偏的, 因为
\[r(1) \not \! \perp \!\!\! \perp o | x, \]故之前的推导就失效了.
本文方法
-
假设我们用逻辑斯蒂回归去拟合 \(\hat{p}\), 即
\[\hat{p}_{u, i} = \mathbb{P}(o_{u, i} = 1| x_{u, i}) = \frac{\exp(m(x_{u,i}))}{1 + \exp(m(x_{u,i}))}, \]其中 \(m(\cdot)\) 是任意的函数;
-
类似地, 用加性模型
\[\tilde{p}_{u, i} = \mathbb{P}(o_{u, i} = 1| x_{u, i}, h_{u,i}) = \frac{\exp(m(x_{u,i}) + \varphi(h_{u, i}))}{1 + \exp(m(x_{u,i}) + \varphi(h_{u,i}))}, \]拟合真实的 propensity score;
-
\(|m(x) + \varphi(h)|\) 的大小和能量有关, 作者假设没观测到 confounders 的能量是有限的, 被控制在 \(|\varphi (h)| \le \log \Gamma, \Gamma \ge 1\), 若 \(\Gamma = 1\), 这意味着不辞你在 confounders;
-
此时
\[\frac{1}{\Gamma} \le \frac{(1 - \hat{p})\tilde{p}}{\hat{p} (1 - \tilde{p})} = \exp(\varphi(h)) \le \Gamma, \]于是
\[a_{u,i} \le \tilde{w}_{u,i} := \frac{1}{\tilde{p}_{u, i}} \le b_{u,i}, \\ a_{u, i} = 1 + (1 / \hat{p}_{u,i} - 1) / \Gamma, b_{u,i} = 1 + (1 / \hat{p}_{u,i} - 1) \Gamma \] -
到此, 我们知道到了 \(\tilde{w}_{u, i}\) 的和 \(\tilde{p}_{u, i}\) 无关的一个上下界, 我们可以从上下界范围内采样合适的点来帮助训练, 作者采取的是对抗训练的思路, 每次采样最恶劣的点:
\[\tag{12} \min_{\phi} \: \mathcal{L}_{RD-IPS}(\phi) = \max_{W \in \mathcal{W}} \frac{1}{|\mathcal{D}|} \sum_{(u, i) \in \mathcal{D}} o_{u, i} e_{u, i} w_{u, i}, \]其中
\[\mathcal{W} := \{W \in \mathbb{R}_+^{|\mathcal{D}|}: a_{u, i} \le w_{u,i} \le b_{u, i} \} \\ \]\(w_{u,i}\) 为 \(W\) 的元素;
-
可以期待, 这种方式使得训练更加鲁棒.
Q: 似乎 (12) 中仅仅取到了上界 ?
注: 作者还提出了一个 BRD (Benchmarked RD Framework) 的版本:
其中 \(e_{u, i}(\hat{\phi}^{(0)})\) 是已有的一个方法的估计结果. 其实细想, 注意到
的时候, \(w_{u, i}\) 取 \(b_{u,i}\), 即因为这部分和 baseline 的结果差的还比较远, 所以加强了权重, 而当
之后, \(w_{u, i}\) 取了 \(a_{u,i}\), 即因为在 \(u, i\) pair 上的表现已经比 baseline 更好了, 所以继续好下去可能反而容易造成过拟合之类的, 所以就加了一个小的权重. 话说这个技术应该有别的论文给出吧.
注: 与其它方法的结合这里就不提了.
代码
[official]
