Towards Representation Alignment and Uniformity in Collaborative Filtering

目录

• 概
• 符号说明
• Alignment and Uniformity
• 本文方法
• 其他
• 代码

Wang C., Yu Y., Ma W., Zhang M., Chen C., Liu Y. and Ma S. Towards representation alignment and uniformity in collaborative filtering. In ACM SIGKDD Conference on Knowledge Discovery and Data Mining (SIGKDD), 2022.

概

作者分析了特征 alignment 和 uniformity 的重要性, 并针对 BPR 进行了改进.

符号说明

• $\mathcal{U}$, user;
• $\mathcal{I}$, item;
• $\mathcal{R} = \{(u, i): u \text{ interacted with } i\}$;
• $f(u), f(i) \in \mathbb{R}^d$, user $u$ 和 item $i$ 所对应的特征;
• $s(u, i)$, u, i 间的 score, 比如用 $f(u)^T f(i)$ 度量;
• BPR:
  $$\tag{1} \mathcal{L}_{BPR} = \frac{1}{|\mathcal{R}|} \sum_{(u, i) \in \mathcal{R}} -\log [\text{sigmoid}(s(u, i) - s(u, i^{-}))]$$
  其中 $i^{-}$ 从 $\mathcal{u} \times \mathcal{I} \setminus \mathcal{R}$ 中随机采样;

Alignment and Uniformity

将 (1) 进行解剖, 可以得到

$$\begin{array}{ll} -\log [\text{sigmoid}(s(u, i) - s(u, i^{-}))] &=-\log \frac{e^{s(u, i)}}{e^{s(u, i)} + e^{s(u, i^{-})}} \\ &=-s(u, i) + \log (e^{s(u, i)} + e^{s(u, i^{-})}) \\ &\rightarrow -\mathbb{E}_{(u, i) \sim p_{pos}} s(u, i) + \log \mathbb{E}_{(u,i) \sim p_{data}} (e^{s(u, i)}), \\ \end{array}$$

若令

$$s(u, i) := -\|f(u) - f(i)\|^2,$$

则上式大约等价于

$$\tag{2} l_{\text{align}} = \mathbb{E}_{(u, i) \sim p_{pos}} \|f(u) - f(i)\|^2,$$

$$\tag{3} l_{\text{uniform}} = \log \mathbb{E}_{(u, i) \sim p_{data}} e^{-2 \|f(u) - f(i)\|^2},$$

其中 $p_{pos}, p_{data}$ 分别表示 positive pair 间的分布, 和一般 pair 的分布.

虽然 BPR 损失的设计的确是兼顾了 alignment 和 uniformity, 使得 positive pair 之间互相靠近, 而 negative pair 间互相远离, 但是在实际情况中, 并非如此理想, 如下图所示:

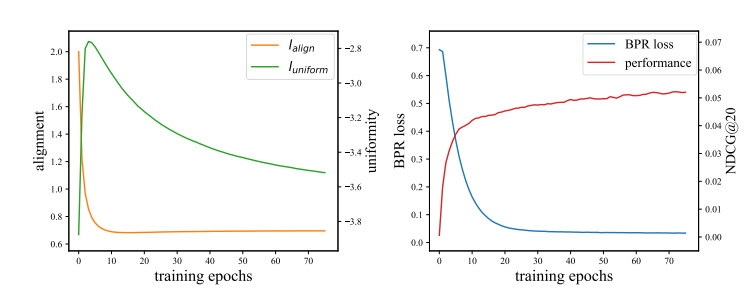
利用最普通的 MF 方法和 BPR 损失, 从上左图可以看见, $l_{\text{align}}$ 会迅速下降, 即整体的 alignment 会迅速满足, 而代价是 uniformity 先增加再渐渐降低.

作者进一步在 BPRMF, BPR-DS, LGCN, ENMF 上进行实验, 发现兼顾 alignment 和 uniformity 的方法往往具有更好的表现. 此外, 普通的 BPR 本身是很难保证特别好的 alignment.

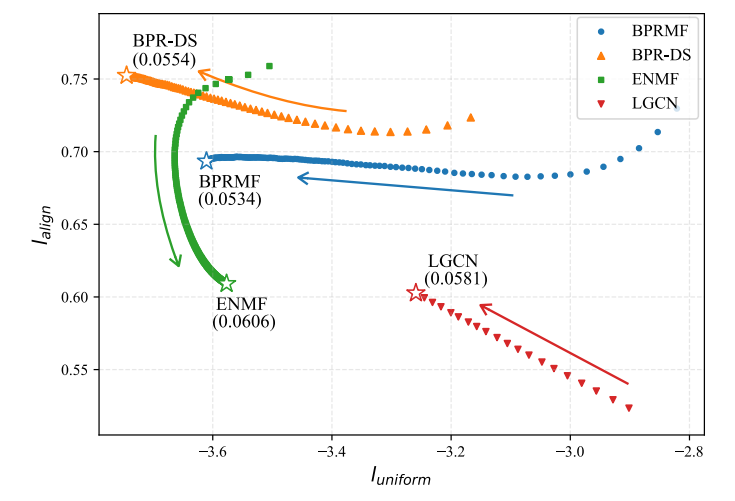
本文方法

1. 对于 $(u, i)$ 通过映射 $f(\cdot)$ 得到他们的特征表示:

   $$f(u), f(i).$$

   特别地, 作者直接采取 $f(\cdot)$ 为一 embedding table 加之 l2 normalization. 即假设 $e_{u}$ 为 $u$ 的 embedding, 取

   $$f(u) = \frac{e_u}{\|e_u\|},$$

   虽然可以用更复杂的 encoder 来代替, 但是作者发现复杂的 encoder 所带来的提升并没有太多;

2. 利用如下损失训练:

   $$l_{\text{align}} = \mathbb{E}_{(u, i) \sim p_{pos}} \|f(u) - f(i)\|^2, \\ l_{\text{uniform}} = \log \mathbb{E}_{(u, u') \sim p_{\text{user}}} e^{-2 \|f(u) - f(u')\|^2} / 2 +\log \mathbb{E}_{(i, i') \sim p_{\text{item}}} e^{-2 \|f(i) - f(i')\|^2} / 2, \\ \mathcal{L}_{\text{DirectAU}} = l_{\text{align}} + \gamma l_{\text{uniform}}.$$

大致如下图所示:

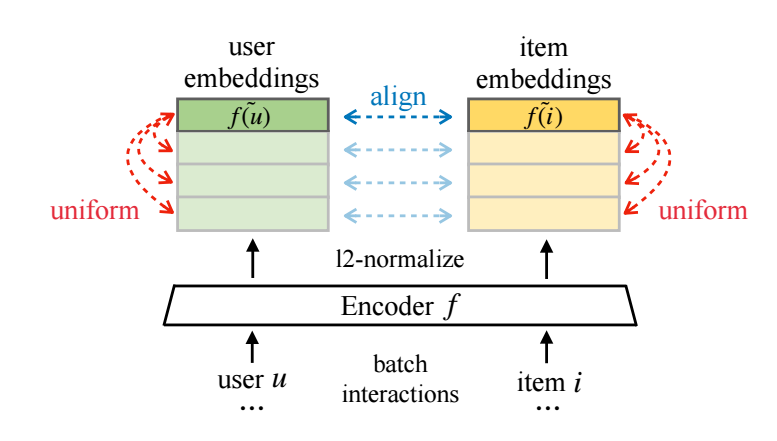
其他

作者还理论证明了 BPR 对于 Alignment 和 Uniformity 的倾向 (感觉并无意义), 感兴趣的不妨回看原文.

代码

[official]