PiCIE: Unsupervised Semantic Segmentation using Invariance and Equivariance in Clustering

目录

• 概
• 符号说明
• 流程
• 代码

Cho J., Mall U., Bala K. and Hariharan B. PiCIE: unsupervised semantic segmentation using invariance and equivariance in clustering. In IEEE Conference on Computer Vsion and Pattern Recognition (CVPR), 2021.

概

利用聚类和 invariance to photometric transformations and equivariance to geometric transformations 来无监督地语义分割.

符号说明

• $x_i \in \mathbb{R}^{CHW}, i=1,2,\cdots, n $, unlabeled images;
• \(f_{\theta}: \mathbb{R}^{CHW} \rightarrow \mathbb{R}^{DHW}\), 将图片 \(x\) 映射为后续所用的特征;
• \(y_{i}[p]\), 为 \(x_{i}[p]\) 所对应的(预测)标签;
• \(\mu_k \in \mathbb{R}^D, k=1,2,\cdots, K\), 为 \(K\) 个聚类中心;
• \(P\), photometric 变换, 满足 \(x, P(x)\) 的语义分割是一致的;
• \(G\), geometric 变换, 满足 \(G(x)\) 的语义分割为 \(G(y)\);

流程

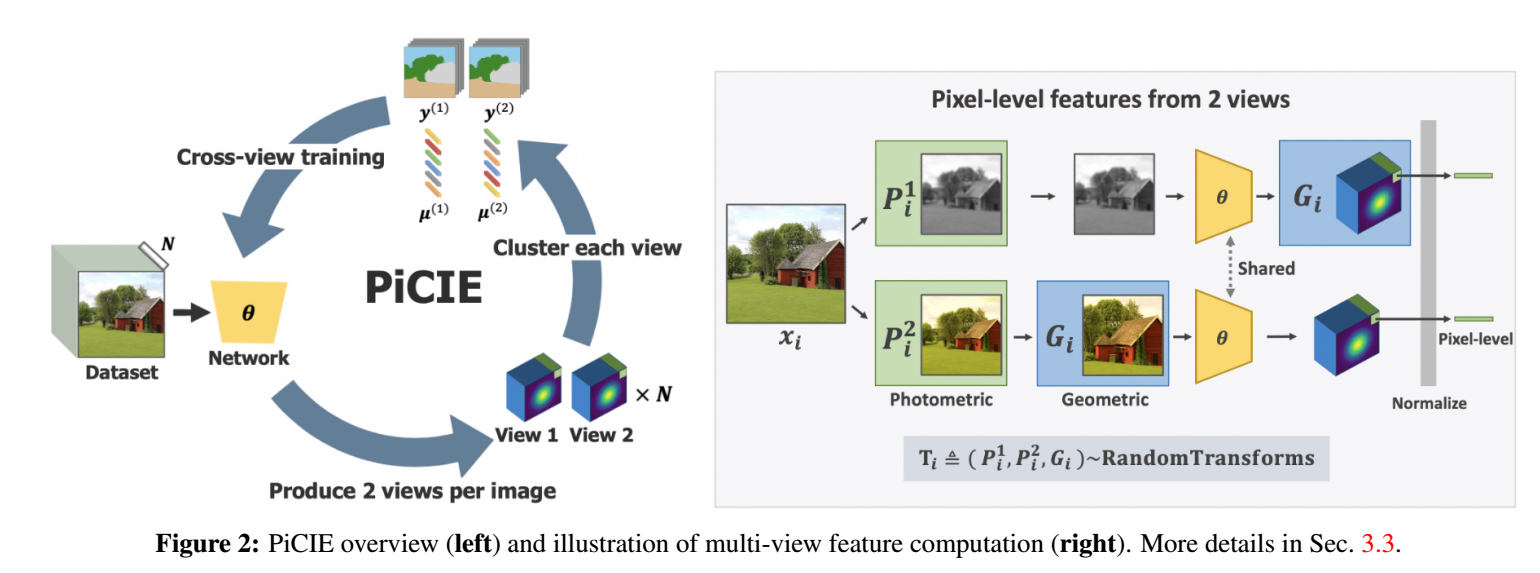
1. 采样样本 \(x\), photometric 变换 \(P^{(1)}, P^{(2)}\), geometric 变换 \(G\);

2. 得到特征:

   \[z^{(1)} \leftarrow G (f_{\theta}(P^{(1)}(x))), \\ z^{(2)} \leftarrow f_{\theta}(G(P^{(1)}(x))); \\ \]

3. 通过 K-means 计算类别中心, 并为 \(z_i[p]\) 指定标签:

   \[\mu^{(1)}, y^{(1)} \leftarrow \text{KMeans}(\{z_i^{(1)}[p]: i \in [n], p \in [HW] \}), \\ \mu^{(2)}, y^{(2)} \leftarrow \text{KMeans}(\{z_i^{(2)}[p]: i \in [n], p \in [HW] \}); \\ \]

4. 我们希望特征 \(z[p]\) 靠近所指定的类别, 即需要关于 \(\theta\) 最小化如下损失:

   \[\mathcal{L}_{within} = \sum_{i, p} \mathcal{L}_{clust}(z_{i}^{(1)}[p], y_{i}^{(1)}[p], \mu^{(1)}) + \mathcal{L}_{clust}(z_{i}^{(2)}[p], y_{i}^{(2)}[p], \mu^{(2)}), \]

   其中

   \[\mathcal{L}_{clust}(z_i[p], y_i[p], \mu) := -\log \frac{\exp(-d(z_i[p], \mu_{ip}))}{\sum_{k} \exp(-d(z_i[p], \mu_{k}))}, \]

   以及 \(d(\cdot, \cdot)\) 为 cosine similarity;

5. 但是注意到, 即便 \(z\) 中的各个元素都靠近了各自的聚类中心, 我们没法保证聚类是按照 '语义' 来分割的, 为此, 我们引入 Invariance 和 Equivariance:

   \[\mathcal{L}_{cross} = \sum_{i, p} \mathcal{L}_{clust}(z_{i}^{(1)}[p], y_{i}^{(2)}[p], \mu^{(2)}) + \mathcal{L}_{clust}(z_{i}^{(2)}[p], y_{i}^{(1)}[p], \mu^{(1)}), \]

   即采用了 photometric 和 geometric 变换后的特征保持语义分割上的一致.

代码

[official]