Variational Autoencoders for Collaborative Filtering

目录

• 概
• 整体框架
• 细节
• 代码

Liang D., Krishnan R. G., Hoffman M. D. and Jebara T. Variational autoencoders for collaborative filtering. In International Conference on World Wide Web (WWW), 2018.

概

一种基于 VAE 的协同过滤方法.

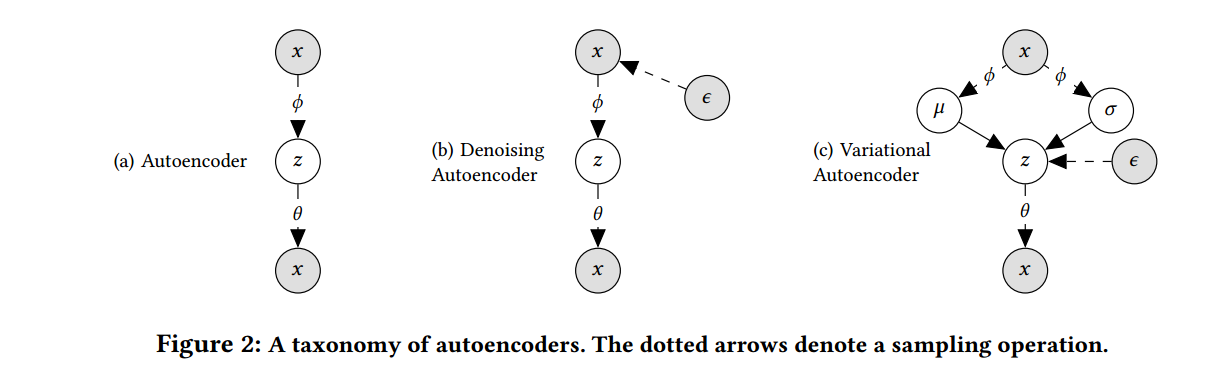
整体框架

1. $\bm{x}_u \in \mathbb{R}^I$, 用户 $u$ 所对应的一个历史点击情况;

2. 经过编码器 $g_{\phi}$ 得到:

   $$[\mu_{\phi}(\bm{x}_u), \sigma_{\phi}(\bm{x}_u)] \in \mathbb{R}^{2K},$$

   其中 $K$ 代表隐变量的维度;

3. 基于二者构建后验分布:

   $$q_{\phi}(\bm{z}_u|\bm{x}_u) := \mathcal{N}(\mu_{\phi}(\bm{x}_u), \text{diag}(\sigma_{\phi}^2 (\bm{x}_u))),$$

   并通过重参数化进行采样

   $$\bm{z}_u = \mu_{\phi}(\bm{x}_u) + \epsilon \odot \sigma_{\phi}(\bm{x}_u), \: \epsilon \sim \mathcal{N}(\bm{0}; \bm{I}_K);$$

4. 通过解码器 $f_{\theta}$ 得到概率向量

   $$[\pi(\bm{z}_u)]_i := \frac{[\exp(f_{\theta}(\bm{z}_u))]_i}{\sum_j [\exp(f_{\theta}(\bm{z}_u))]_j}, \: i=1,2,\cdots, I;$$

   假设 $\hat{\bm{x}}_u | \bm{z}_u$ 服从多项式分布:

   $$p(\hat{\bm{x}}_u | \bm{z}_u) := \text{Mult}(N_u, \pi(\bm{z}_u)),$$

   其中 $N_u = \sum_i [\hat{\bm{x}}_u]_i$ 表示推荐的次数.

5. 最大化 ELBO 进行训练:

   $$\mathcal{L}_{\beta}(\bm{x}_u; \theta, \phi) = \mathbb{E}_{q_{\phi}(\bm{z}_u | \bm{x}_u)} [\log p_{\theta}(\hat{\bm{x}}_u = \bm{x}_u|\bm{z}_u)] - \beta \cdot \text{KL} (q_{\phi}(\bm{z}_u| \bm{x}_u) \| p(\bm{z}_u)),$$

   其中 $\beta = 1$ 表示原始的 ELBO, 这里显式添加 $\beta$ 用于后面方便调节, 作者采用了 $\beta$ 从 $0$ 逐渐升至 $0.2$ 的方式调节. 此外 $p(\bm{z}_u)$ 表示先验分布, 通常为普通的标准正态分布.

6. 实际推断的时候, 只需计算 $f_{\theta}(\bm{z}_u)$, 然后找到 top-k 作为推荐即可 (即概率越大越应该被推荐).

注:

$$\log p_{\theta}(\bm{x}_u|\bm{z}_u) = \sum_i [\bm{x}_u]_i \log [\pi (\bm{z}_u)]_i.$$

细节

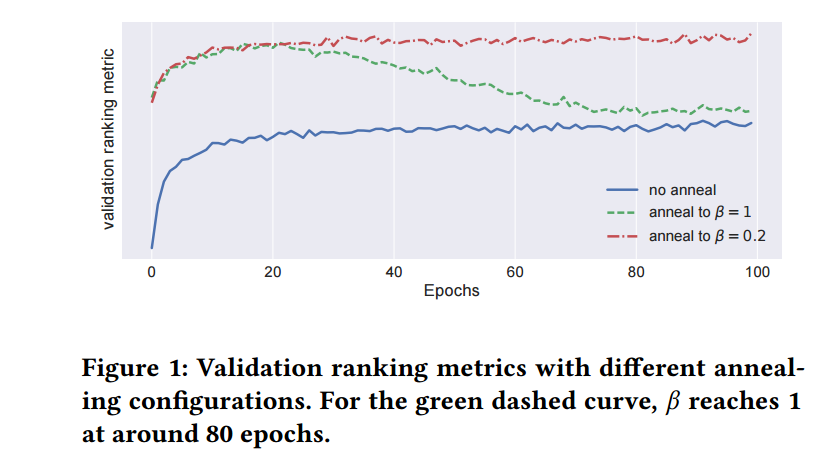
如图, 恒定 $\beta=1$ 或者 $\beta$ 从零逐步上升到 $1$ 最后的结果都不是太好, 逐步升到 $\beta=0.2$ 是结果最好的.

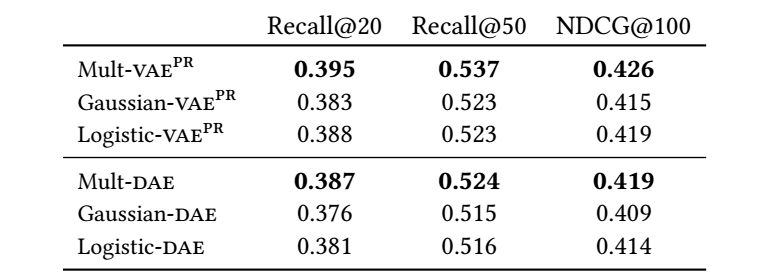
作者也试了不同的 $p(\hat{\bm{x}}_u|\bm{z}_u)$ 的构建, 比较下来是多项式分布最优.

代码

[official]