Bareinboim E., Correa J. D., Ibeling D. and Icard T. On pearl’s hierarchy and the foundations of causal inference. 2021.
概
这部分内容主要介绍 PCH 中的三个阶段 Li,i=1,2,3. 并介绍在什么情况下, 我们可以通过 L1 推测 L2, 即利用观测数据进行因果推断.
符号说明
- X, 随机变量;
- Val(X), 值域;
- x∈Val(X), 某个取值;
- X, 一组随机变量;
- P(Yx):=P(Y|do(X=x));
- path (X,Y): X 到 Y 的路径 (不限方向, 比如 X←U→Y 也是 ok 的);
- collider: Z 为 X,Y 的 collider X→Z←Y, 仅仅此模型而言:
X⊥⊥Y,X/⊥⊥Y|Z.
Structural Causal Models and the Causal Hierarchy
Structural Causal Model (SCM)
SCM M 由四元组 ⟨U,V,F,P(U)⟩ 所定义, 其中
-
U 为外部的 (exogenous) 背景 (backgroud) 元素, 通常是不感兴趣的或者难以观测的变量构成;
-
V={V1,V2,⋯,Vn} 则是内部的 (endogenous) 由其它结点 (父节点) 所决定的变量;
-
关系 F={f1,f2,⋯,fn} 将 Ui⋃Pai 映射为结点 Vi, 这里 Ui 是与 Vi 关联的外部结点, 而 Pai⊂V 则是 Vi 的父节点, 即
vi←fi(pai,ui);
- P(U) 是外部节点 U 的分布.
注: 这里假设 SCM 是 recursive, acyclic 的, 即若 fi≺fj (这里 ≺ 代表'时序'), 则 fi 的输入不包含 Vj.
注: 给定 U, 则 V 也就知道了, 故整个系统由 U 和 F 决定.
Causal Hierarchy
Pearl 将人认知的三个过程: seeing, doing, imagining 抽象为 association, intervention, and counterfactual 三个阶段 (分别记为 L1,L2,L3)
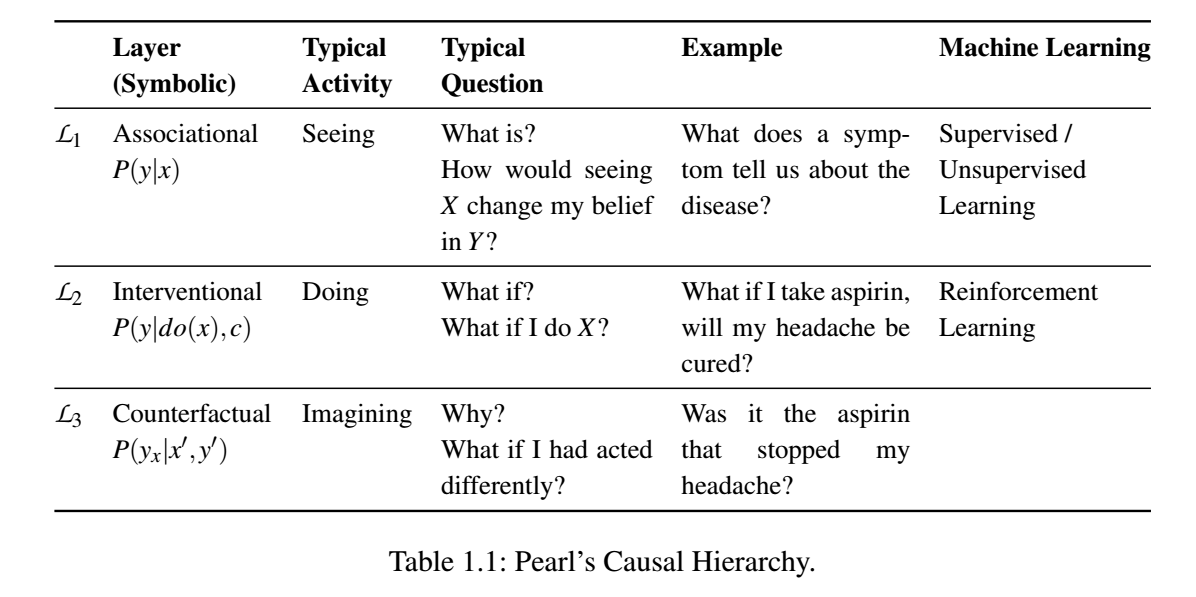
Layer1-Seeing
对于任意的 SCM M, 可以通过下式
PM(Y=y)=∑{u|Y(u)=y}P(u)(L1)
估计出任意 Y⊂V 的联合分布. 其中 Y(u) 给定 U=u 后 Y 的值.
实际上, 现在大抵的机器学习就是为了估计数据的一个联合分布. 比如:
- 图像生成: V=Z⋃X, 其中 X 为图像, Z 为一些属性, 然后只要估计出
P(X|Z)
就可以采样图片了;
- 分类任务: V=X⋃Y, 其中 X 为图片, Y 为标签, 则一般的分类模型实际上就是建模
P(Y|X).
总的来说, 这些任务依旧停留在数据分布估计之上.
Layer2-Doing
我们常常做出假设并验证. 若我们希望考察如果设定 X=x 下其它结点的情况, 此时相当于构建了一个新的 SCM:
Mx=⟨U,V,Fx,P(U)⟩,
其中
Fx={fi:Vi∉X}∪(X←x).
此时, 我们可以通过下式估计
PM(Yx=yx)=∑{u|Yx(u)=yx}P(u)(L2)
其中 Yx(u) 表示在 Fx 和 U=u 下的结果.
Layer3–Imagining
吾日三省吾身. 人是非常擅长从反省中进步的, 比如考完试后, 总会想如果某个题再看仔细点会如何如何. 在这过程中, 我们将真实的世界所发生的事情和虚构的世界发生的事情联系了起来, 而且虚构的世界往往给予现实之上的. 这实际上是面对:
P(Y′x′|X=x,Y=y)
的估计问题. 即在观测到现实中 X=x,Y=y 的事实后, 思考在 do(X=x′) 的条件下的结果.
一般来说 (看下面的例子), 我们只需要构建出 Yx,Yx′⋯ 的联合分布, 上式也是水到渠成的事情. 而对于 任意的 Y,Z,⋯,X,W⊂V, Yx,⋯,Zw 的联合分布为
PM(yx,⋯,zw)=∑{u|Yx(u)=yx,⋯,Zw(u)=z}P(u).(L3)
注: Yx,⋯,Zw 实际上是不同虚构世界中的元素, 故 (L3) 构建了这样的一个联系;
注: (L3) 其实很好理解, 把 U 看成最底下的水源, 上面是借此生长的花花草草, 无论多复杂, 只要寻到了底下的 atom, 一切就迎刃而解了.
注: 在实际中, 我们需要通过 Mx,Mw 分别求解 {u|Yx(u)=yx}⋯, 然后取交集.
例子
假设存在如下的一个模型:
V={X,Y,Z}U={Ur,Ux,Uy,Uz}F={fx,fy,fz}.
一个病人患了某种病, 有可能表现出一些症状, 如头疼 (Z=1), 也有可能没有症状 (Z=0), 根据症状和其它因素, 医生会选择是否开药 (X∈{1,0}). 病人最后是否能够康复受其是否自身的抵抗力 Ur∈0,1, 是否开药 X 以及未知因素 Uy 影响. 具体来说, X,Y,Z 的值可通过下式推导出:
fz:Z←IUr=1,Uz=1fx:X←I{Z=1,Ux=1}∨{Z=0,Ux=0}fy:Y←I{X=1,Ur=1}∨{X=0,Ur=1,Uy=1}∨{X=0,Ur=0,Uy=0}.
仅从上式我们可以得出结论: 对那些有免疫力的人 (Ur=1) 开药 (X=1) 是有利的 (Y=1), 对没有免疫力的人开药反而是有害的.
接下来, 我们考察在
P(Ur=1)=0.25,P(Uz=1)=0.95,P(Ux=1)=0.9,P(Uy=1)=0.7
的条件下, 三种层次所得出来的结论.
- Seeing: 根据 (L1) 可以算出来:
P(Y=1|X=0)=0.3197,P(Y=1|X=1)=0.7414.
所以从条件概率的角度来讲, 该药物对于治疗该疾病是有利的;
- Doing: 保持 fz,fy 不变, 令 fx:X←1 可得:
P(Y=1|do(X=1))=0.25.
类似地, 令 fx:X←0 可得:
P(Y=1|do(X=0))=0.4.
所以其得出的结论是该药物对于治疗该疾病是无效的.
- 接下来, 通过 imagining 可以进一步回答这个问题. 通过 (L3) 可得
P(YX=1=1,X=0,Y=0)=0.0105,
再通过 (L1) 可得:
P(X=0,Y=0)=0.483,
通过贝叶斯公式可得:
P(YX=1=1|X=0,Y=0)=0.01050.483=0.0217,
即无法自愈的个体即使给药了也通常无法康复. 类似地,
P(YX=1=1|X=0,Y=1)=0.01050.483=0.1079,
能够自愈的个体, 给药后反而无法康复. 故通过 Layer3 我们最终得到了我们所希望的结论.
Expressivity of Pearl Causal Hierarchy (PCH)
通过上面的分析我们可知, 只要知道 SCM M, 那么各层 Li,i=1,2,3 的信息也就容易求得了. 而且显然, 这三者所包含的信息量是
L1≺L2≺L3
的 (因为低层的均可以看成是高层的一个特例).
但是这个顺序是直观上的, 并不严谨. 思考一个有趣的例子, 我们知道, 整数, 有理数, 实数也是类似的一种从低到高的关系(从包含数的角度上讲), 但是它们的基数却是 整数=有理数<实数. 虽然整数真包含在有理数中, 但是我们可以找到一个一一映射, 换言之, 二者的表达能力是一致的.
那么现在的问题是, 虽然 L1,L2,L3 有上面的关系, 会不会和整数, 有理数一样实际上所包含的信息量是一致的呢? 倘若是的话, 那么我们就没有研究高层的必要了. 再通俗点讲, 倘若通过 L1 能够推出 L2 甚至 L3, 那么意味着普通的数据就能帮助我们进行因果推断了. 答案自然是否定的.
等价类定义
∼i: 假设 Ω 为一包含感兴趣的 SCM 的集合, 对于任意的 M,M′∈Ω, 我们称二者是 Li 等价的, 即 M∼iM′, 若二者在 Li 上是一致的.
注: 文中用的是逻辑语言来度量一致性, 从我的角度来看, 比如 L1 上一致, 就是联合分布 P(V) 是相同的, 而 L2 上一致, 就是 P(Yx)∀Y⊂V,X=x 是相同的.
Collapse
Collapse relative to M∗:, 对于 SCM M∗∈Ω, 称其 Lj 塌缩为 Li,i<j, 若
M∗∼iM→M∗∼jM,∀M∈Ω.
一旦 Lj 塌缩为 Li, 比如 L2 塌缩为 L1, 这就意味着, 所有能够导出 L1 的 SCM M 均导出相同的 L2. 此时想要通过 L1 获得 L2, 我们可以:
- 构建任意满足 L1 的 M;
- 通过 M 得到 L2.
这就相当于, L1 包含了构建 L2 所需的全部信息, 此时我们只需要研究 L1, 即简单的观测数据即可了.
Causal Hierarchy Theorem (CHT)
Causal Hierarchy Theorem (CHT): 对于 SCMs Ω, 其中会发生塌缩的子集的 Lebesgue 测度为 0.
注: Lebesgue 测度的定义, 首先需要对 SCMs 进行一个编码, 使其称为落在一个 [0,1]K 中的一个凸集 (等有时间看了该作者另外一篇文章的证明就知道了).
CHT 说明了, 会发生塌缩的 SCM 几乎是不存在的. 这也就说明了研究 L2 以及 L3 的必要性.
Corollary 1: 想要回答 Li 所构建的问题, 需要知道 Li 或者更高层次的 Lj,j>i 的信息.
例子
我们仍以上一节的例子为例 (记为 M∗). 我们令 (记为 M)
fy:Y←I{Ur=1,Ux=1,Uz=1}∨{Ur=1,Ux=0,Uz=0}∨{Ur=1,Ux=0,Uy=1,Uz=1}∨{Ur=1,Ux=1,Uy=0},
其余的映射保持不变. 此时, X,Y 之间并不存在直接的因果关系, 即
PM(Y|do(X=x))=PM(Y).
即 L2 层面, 两个 SCMs 是不等价的. 但是可以计算得到, L1 层面二者是等价的. 这就说明了, 在这个这个例子中, 仅通过观测数据是无法进行 do 操作的.
还可以构造出 L1,L2 等价的 M′ 但是 L3 不等价 (详情见文中 Example 9).
基于数据的因果推断
诚然, 倘如我们能够知道 SCM M 本身, 那么无论是 Li,i=1,2,3 的问题就都迎刃而解了. 但是在实际中, 我们通常只有可怜的观测数据可以用, 即
P(V)
是可知(估计)的. 而我们又从上一节的 CHT 知道, 仅通过 L1 的信息想要推断出 L2,L3 几乎是不可能的. 于是现在的问题是, 通过添加怎么样的额外信息, 能够帮助我们进行 L2 甚至是 L3 层面的推断呢?
[不可行] Layer1 的约束
我们先来看看一种常用的但是实际上不可行的 L1-约束: 条件独立 (conditoinal independence). 直接以例子进行佐证.
考虑 V={X,Z,Y},U={Ux,Uy,Uz}, 而 M1,M2 分别由
F1=⎧⎪⎨⎪⎩fx:X←Uxfz:Z←X⊕Uzfy:Y←Z⊕UyF2=⎧⎪⎨⎪⎩fx:Z←Z⊕Uxfz:Z←Y⊕Uzfy:Y←Uy.
其中 ⊕ 代表 xor 且
P1(Ux=1)=P2(Uy=1)=1/2P1(Uz=1)=P2(Ux=1)=aP1(Uy=1)=P2(Uz=1)=b.
容易证明, M1, M2 导出相同的 L1, 即
P1(V)=P2(V).
同时, 都满足条件独立性:
X⊥⊥Y|Z.
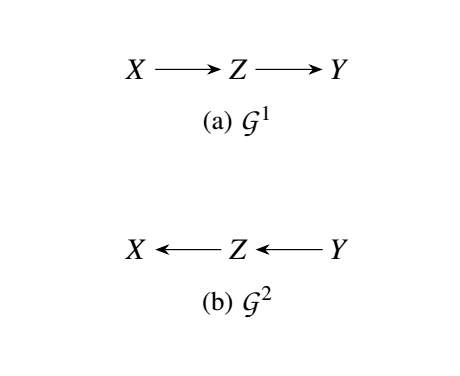
但是, 它们的 L2 层面的性质, 比如
P1(Y=1|do(X=1))=ab+(1−a)(1−b),P2(Y=1|do(X=1))=1/2,
就不一致了.
这说明, 即使加了合理的条件约束, 依然无法保证 L2 是正确的.
Layer2 约束 - Markovian Causal Bayesian Networks
Causal Diagram (Markovian Models): 考虑一个 Markovian SCM M=⟨U,V,F,P(U)⟩. 则其 casual diagram G 通过如下方式定义:
- 所有的内部结点 V 为顶点;
- 添加有向边 Vj→Vi, 一旦 Vj 为 fi 的是一个直接的参数, 即
Vi=f(⋅,⋯,Vj,⋯).
CBN - Markovian
Causal Bayesian Network (CBN - Markovian): 令 P∗ 为所有 interventional distributions P(V|do(x)),X⊂V,x∈Val(X). 则有向无环图 G 称为 P∗ 的 Causal Bayesian Network, 如果对于所有的 X⊂V 有下列性质成立:
- [Markovian] P(V|do(x)) 满足马尔可夫性质, 即
P(Vx)=∏Vi∉XP(vi|pai,do(x)).
即给定其父节点 pai, Vi 与其非后代结点独立.
- [Missing-link] 对于任意的 Vi∈V,Vi∉X, 则
P(vi|do(pai),do(x))=P(vi|do(pai)).
在固定(doing)父节点之后, do(X) 就不起作用了.
- [Parent do/see] 对于任意的 Vi∈V,Vi∉X:
P(vi|do(x),do(pai))=P(vi|do(x),pai).
注: 条件 2, 3 等价于 [Modularity]:
P(vi|do(x),pai)=P(vi|pai).
proof:
[Missing-link] + [Parent do/see] ⇒ [Modularity]:
P(vi|do(x),pai)=P(vi|do(x),do(pai))=P(vi|do(pai))=P(vi|pai).
[Parent do/see] ⇐ [Modularity]:
P(vi|do(x),do(pai))=∫V∖(X∪pai∪{Vi})P(vi|do(x),do(pai),pai)∏Vj∉X∪pai∪{Vi}P(vj|do(x),do(pai)paj)=∫V∖(X∪pai∪{Vi})P(vi|pai)∏Vj∉X∪pai∪{Vi}P(vj|paj)=P(vi|pai)=P(vi|do(x),pai).
[Missing-link] ⇐ [Modularity]:
P(vi|do(pai),do(x))=P(vi|pai,do(x))←[Parent do/see]=P(vi|pai)←[Modularity]=P(vi|do(pai)).←[Parent do/see].
[Markovian] CBN + Layer1 -> Layer2
倘若我们所关注的 SCM M 是满足 Markovian 的, 即
P(V)=∏P(Vi|Pai).
则其所导出的 casual diagram G 是一个 CBN, 此时我们可以根据 L1 的性质来推导 L2:
P(v|do(x))=∏Vi∉XP(vi|do(x),pai)←[Markovian]=∏Vi∉XP(vi|do(x),do(pai))←[Parent do/see]=∏Vi∉XP(vi|do(pai))←[Missing-link]=∏Vi∉XP(vi|pai)).←[Parent do/see]
于是, 我们只需求出
P(vi|pai)
这一 L1 层的信息即可进行 L2 层的推断了.
Corollary 2 (Back-door Criterion (Markovian)): 在 Markovian 模型中, 对于操作 X 以及导致的输出 Y, 若 Z 阻隔了 X→Y 的路径, 则
P(Y|do(x))=∑zP(Y|x,z)P(z).
注: 切记, 要求 M 是满足 Markovian 的.
个人更加推荐的 causal diagram 表示方法: SWIG
相较于 Pearl 所提出的这种因果图, 我更喜欢 Robins and Richardson (2013) (也可以参考: Causal Inference: What If, p93) 的 Single-world intervention graphs (SWIGs).
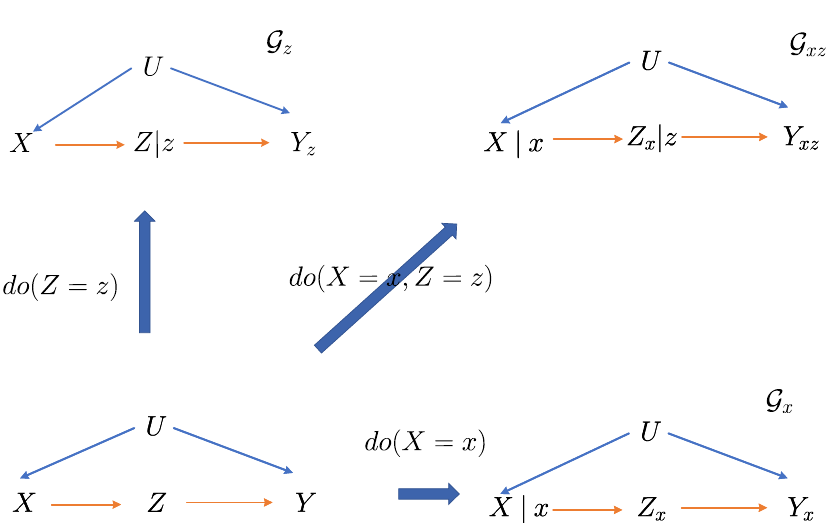
如下图所示, 基于 SCM, do(X=x) 的 SWIG Gx 可以按照如下方式定义:

- 将所有的 U,V 作为顶点;
- 添加 Zj→Zi, 一旦 fi 中的参数包含 Zj;
- 将 X 替换为 X|x, 其中 X|x 显式表示 X,x 无关;
- 将原先由 X 出发的边 → 删除, 并添加相应的由 x→ 出发的边;
- X 的后代 (存在 directed path) 用加上下标 x 以表示 ⋅|do(X=x).
可以发现, 因为我们把未观测的变量 U 也放入了其中, 所以 Gx 实际上是满足 Markov 性质的, 是一个 markovian casual diagram. 此外:
- 如果 X≺Y,
P(X|do(Y))=P(X),
即操作后代对于前者没有影响.
- [Consistency]
P(Y|do(X=x),x)=P(Y,X=x|do(x))/P(X=x|do(x))=P(fY(⋯,X=x,⋯),X=x)/P(X=x)=P(Y|X=x).
Layer2 约束 - Semi-Markovian Causal Bayes Networks
上一节的约束只适用于满足 Markovian 性质的 SCM, 那么怎么样的 M 才会满足这样的性质呢: 那些不存在未观测变量 U 或者不存在同一个 U 同时影响 X,Y∈V 才会满足这个性质. 但是实际上, 这个是很难实现的, 一件事情的发展总会受到各种各样的无法观测因素的干扰.
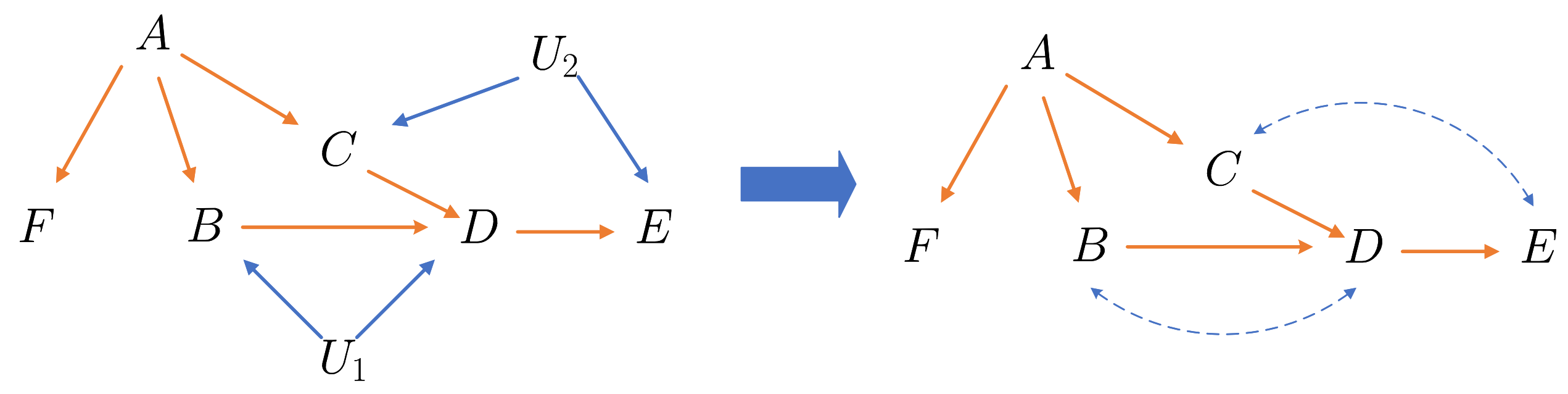
如上图所示, 如果按照 Markovian causal diagram 的定义方式,
P(E|do(D))≠P(E|D),
另外一些 CBN 所需要满足的条件也都是不符合的.
注: 如果能够把所有的 U 考虑进去, 整体还是满足 Markovian 性质的, 即
E⊥⊥{A,B,C,F}|{D,U1,U2}.
但是 U 实际中是未观测的.
Causal Diagram (Semi-Markovian Models): 给定一个普通的 SCM M=⟨U,V,F,P(U)⟩. 则其 causal diagram G 按照如下方式定义:
- 将所有的内部结点 V 作为 G 的顶点;
- 添加有向边 Vj→Vi, 一旦 Vj 为 fi 的是一个直接的参数, 即
Vi=f(⋅,⋯,Vj,⋯).
- 添加双向虚边 Vj⇠⇢Vi, 一旦 fi,fj 共享参数 U∈U, 即
Vi=f(⋅,⋯,U,⋯),Vj=f(⋅,⋯,U,⋯).
如上图所示, 右端就是左端的一个 causal diagram 表示.
既然这种类型的 causal diagram, 即使给定 Vi 的父节点 Pai, 也没有
Vi⊥⊥NDesci|Pai
成立, 其中 NDesci 表示 Vi 的非后代 (non-descendants) 结点. 而这一性质 Markovian 性质对于利用 L1 推导 L2 的信息是至关重要的. 现在的问题是, 我们希望引入'更严格'的条件独立.
Confounded Component: 令 {C1,C2,…,Ck} 为 V 的一个分割 (⋂Ci=∅,⋂Ci=V). Ci 称为 G 的一个 confounded component, 当对于任意的 Vi,Vj∈Ci 之间存在一路径完全由双向虚边 (即 ⇠⇢) 构成, 且 不存在 confounded component C′⊂V,C′≠Ci 且 Ci⊂C, 即 Ci 是最大的了 (maximal).
比如, 上图中:
C1={A},C2={B,D},C3={C,E},C4={F}.
接下来我们观察上例:
E/⊥⊥{A,B,C}|D;
E/⊥⊥{A,B}|{C,D};
注意到, 此时路径 A→C←U→E 由于 |C 而被打通;
E⊥⊥{B}|{A,C,D};
所以, 想要 E 和其非后代结点独立, 需要给定其 父节点 + confounded component + confounded component 的父节点, 即 Pa+E. 其中 Pa+i 定义为
Pa+i:=˜Pa({V∈C(Vi):V⪯Vi})∖{Vi}˜Pa(X):=X∪⋃X∈XPa(X)C(Vi):the confounded component including Vi.
这里 ≺ 表示时序, {V:V⪯Vi} 即表示非后代结点包括 Vi.
Pa+i 的制作过程实际上就是首先收集非后代节点中和 Vi 属于统一 confounded component 的其它点, 然后再合并它们 + 它们的父节点 + Vi 的父节点.
于是我们有如下的类似 Markovian 的定义:
Semi-Markov: 分布 P 称其关于 G (semi-markovian casual diagram) 为 semi-markov 的, 若
P(v)=∏Vi∈VP(vi|pa+i).
假设经过 do(X=x) 后的 causal diagram 为 G¯¯¯¯¯X, 则其满足 semi-markov 若
Px(v)=∏Vi∈VPx(vi|pax+i),
其中 Pax+i 表示根据 G¯¯¯¯¯X 构建的 Pa+i.
注: G¯¯¯¯¯X 是将 G 中指向 X 的边移除后的图.
为什么 do(X) 只需要移除指向 X 即可?
因为此时 X=x 的概率为 1, 以其余的变量无关.
为什么要这么构造 pa+ ? 需要注意的是, Pa+ 实际是一个充分的条件. 注意到:
- Vi 自身的父节点是必须的;
- C(Vi) 也是必须的;
- V∈C(Vi) 的父节点不一定是必须的, 因为可能不存在结点 Vj 指向 Vi, 此时 |V 就不会造成额外的通路了.
例子
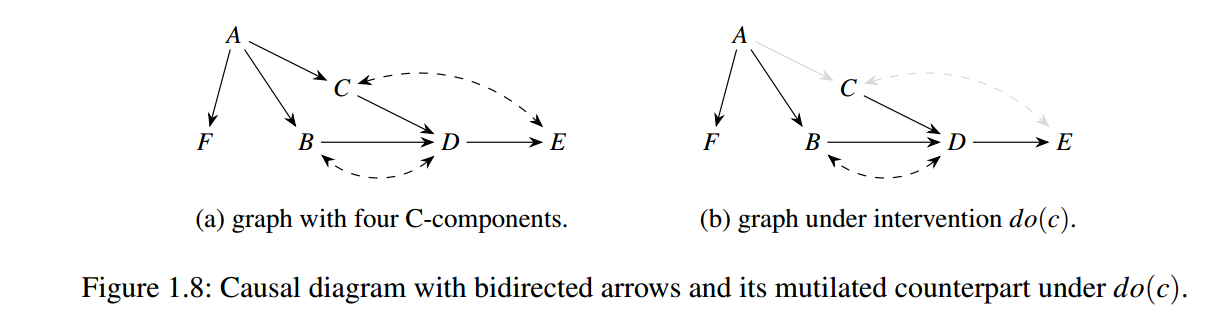
对于上图, 有
A≺B≺C≺D≺E≺F,
根据 semi-markov 性质:
C⊥⊥B|AE⊥⊥B|D,C,AF⊥⊥E,D,C,B|A,
故有
P(a,b,c,d,e,f)=P(a)P(b|a)P(c|a)P(d|a,b,c)P(e|a,d,c)P(f|a).
右图为 do(C=c) 后 G¯¯¯¯C 的表示, 就是将指向 C 的边去掉. 此时有
Pc(a,b,c,d,e,f)=Pc(a)Pc(b|a)Pc(c)Pc(D|c,b,a)Pc(e|d)Pc(f|a).
注: G¯¯¯¯¯X 中的确有:
E⊥⊥{A,B,C}|D,
但是这不意味着:
P(E|do(C),D)=P(E|C,D).
CBN - Semi-Markovian
与 CBN Markovian 类似, 我们给出 CBN - Semi-Markovian 的定义, 并说明这种模型约束下, 我们可以连接一般的 L1 和 L2.
Causal Bayesian Network (CBN - Semi-Markovian): 令 P∗ 为所有 interventional distributions P(V|do(x)),X⊂V,x∈Val(X). 则有向图 G 称为 P∗ 的 Causal Bayesian Network, 如果对于所有的 X⊂V 有下列性质成立:
- [Semi-Markovian] P(V|do(x)) 关于 G¯¯¯¯¯X 是 semi-Markov 的;
- [Missing directed-link] 对于任意的 Vi∈V∖X,W⊆V∖(Pax+i∪X∪{Vi}:
P(vi|do(x),pax+i,do(w))=P(vi|do(x),pax+i).
即给定 pax+i, 再设定非后代结点 W 是无意义的;
- [Missing bidirected-link] 对于任意的 Vi∈V∖X, 假设 Pax+i 可以分割成 confounded (Paci∈C(Vi)) 和 unconfounded (Paui∉C(Vi)) 父节点, 则
P(vi|do(x),paci,do(paui))=P(vi|do(x),paci,paui)).
注: 个人感觉 X,W 没必要区分的如此细致, 这里只是为了避免一些不必要的说明.
以上面的例子来说:
[Missing directed-link]:
P(d|do(f,e),b,c,a)=P(d|b,c,a)P(d|do(b,c),do(a,f,e))=P(d|do(b,c)).
第二个不是应该直接用 f 来思考?
[Missing bidirected-link]:
P(e|do(d))≠P(e|d)P(e|do(a,d),c)=P(e|a,c,d)P(d|do(b,a,c))=P(d|do(b),a,c)
可以证明的是, 一般的 SCM M 所导出的 causal diagram G 都是 semi-Markovian CBN.
[Semi-Markovian] CBN + Layer1 -> Layer2
现在, 给定 Semi-Markovian CBN 结合 L1 的信息, 在有些时候就可以顺利推导出 L2 的信息了, 其所需要用到的工具就是下面的 do-calculus:
Do-Calculus: 令 G 为 P∗ 的一个 CBN, 则 P∗ 满足如下的规则. 即对于不交的 X,Y,Z,W⊆V, 有
- Rule1:
P(y|do(x),z,w)=P(y|do(x),w)if (Y⊥⊥Z|X,W) in G¯¯¯¯¯X.
- Rule2:
P(y|do(x),do(z),w)=P(y|do(x),z,w)if (Y⊥⊥Z|X,W) in G¯¯¯¯¯XZ––.
- Rule3:
P(y|do(x),do(z),w)=P(y|do(x),w)if (Y⊥⊥Z|X,W) in G¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯XZ(W).
其中 ¯¯¯¯¯X 是指移除指向 X 的边, Z–– 是指移除由 Z 发出的边, Z(W) 表示 Z 中不为 W 祖先 (non-ancestors) 的点的集合.
一个尝试性证明 (其实回看 Pearl 的论文比较好).
proof:
Rule1:
因果图 SWIG GX, 可以发现:
如果
Y⊥⊥Z|X,W in G¯¯¯¯¯X,
但是
Yx/⊥⊥Z|W in GX.
则, 在 GX|W 中存在 Z,X,Y 的一个 (经过 X)的 unblocked path, 但是注意到 GX 中 X 所以向外的作用都被 x 替代了, 故存在 unblocked path 的变量 Z∈Z 必须为某个 X∈X 的祖先, 即 Z≺X. 但是任何 X 到 Y 的通路都必须经过其祖先 X←U 实现, 此时 Z→X←U 构成了 collider, 在不给定 |X 的条件下是不可能构成 unblocked path 的.
Rule2:
Rule2 实际上就是证明给定
(Y⊥⊥Z|X,W) in G¯¯¯¯¯XZ––
的条件下成立
(Yxz⊥⊥Z|W) in Gxz.
只需注意到
[Gxz]¯¯¯¯¯X
和
G¯¯¯¯¯XZ––
除 x,z 外的等价性, 再结合 Rule1 便得证了.
Rule3:
记 Za,Zd 分别为 W 的祖先和后代, 让我们首先观察
(Y⊥⊥Z|X,W) in G¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯XZ(W)
代表了什么:
(Y⊥⊥Zd|X,W) in G¯¯¯¯¯¯¯¯¯¯¯XZd
表示 G 中 Zd 要么不存在到 Y 的通路, 或者通路经过 X;
(Y⊥⊥Za|X,W) in G¯¯¯¯¯¯¯¯¯¯¯XZd
Za 到 Y 要么没有通路, 要么经过 W 或 X, 换言之,
Za⊥⊥Yx,z|Win GxzaZa⊥⊥Yx|Win Gx.(cond2)
故在 Gxz 中,
Yxzazd=Yxza
既然 zd 必须通过 X 才能影响 Y, 而 do(X=x) 彻底阻断了这一点, 此时有
P(Y|do(x),do(za,zd),w)=P(Y|do(x),do(za),w)
- 则
P(Y|do(x),do(za,zd),w)=P(Y|do(x),do(za),w)←1=P(Y|do(x),do(za),w,za)←(cond2)=P(Y|do(x),w,zd)←consistency=P(Y|do(x),w).←(cond2)
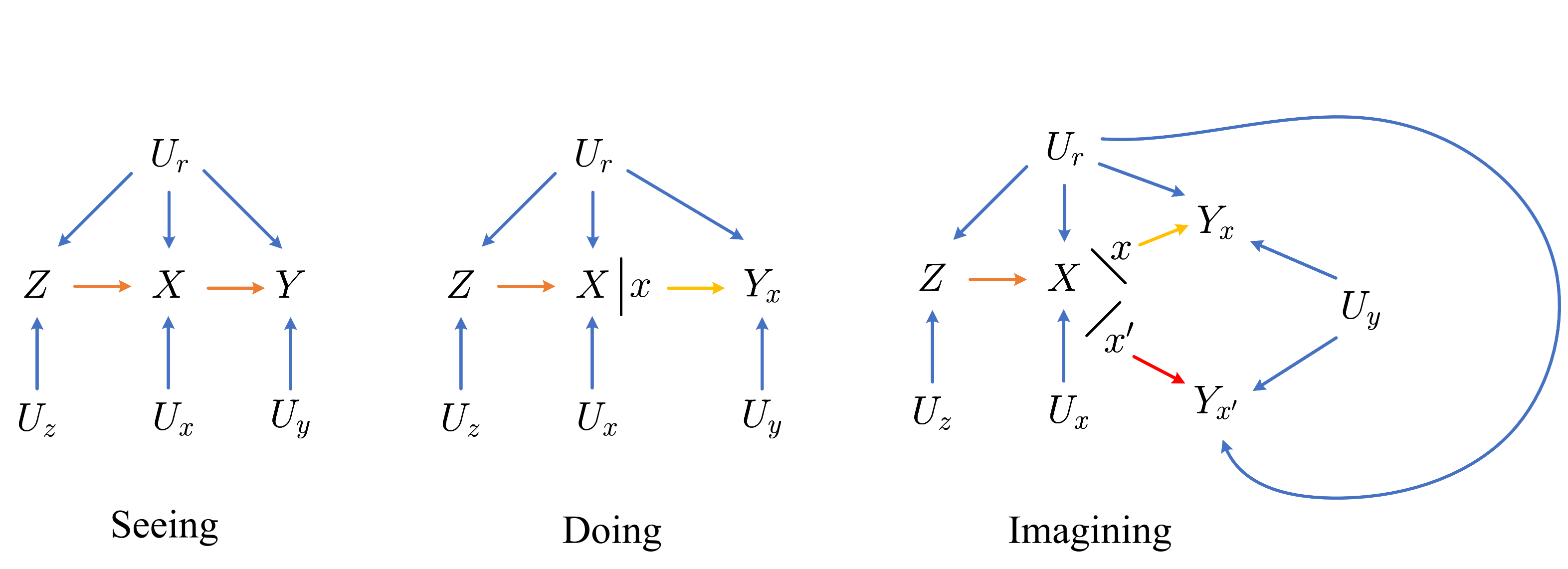
例子
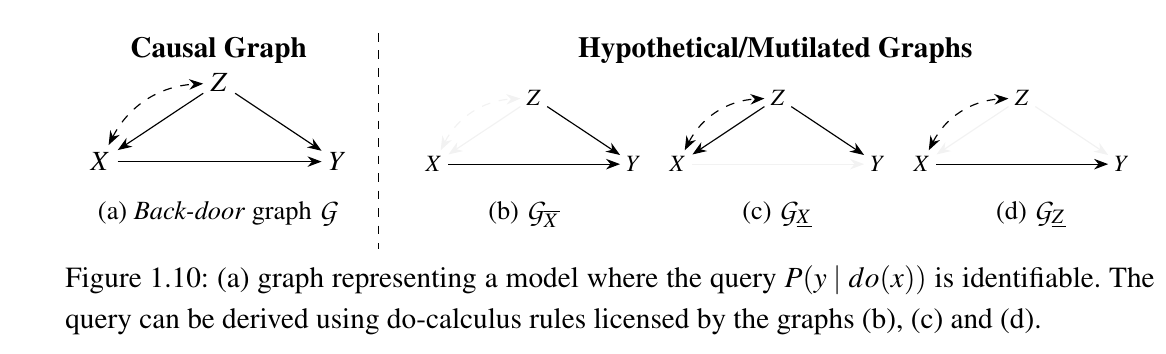
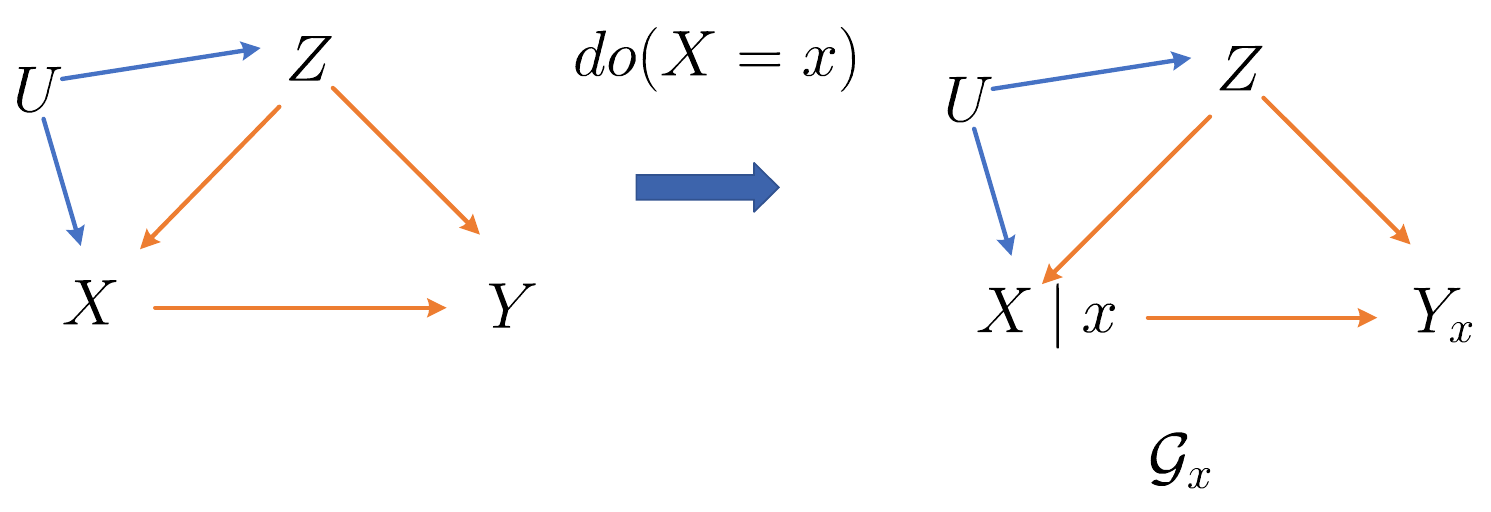
如上图所示, 我们分别用上面介绍的 rules 和 SWIG 来推导 P(y|do(x)):
rules:
P(y|do(x))=∑zP(y|do(x),z)P(z|do(x))=∑zP(y|do(x),z)P(z)←rule3:(Z⊥⊥X)G¯¯¯X=∑zP(y|x,z)P(z)←rule2:(Y⊥⊥X|Z)GX––.
SWIG:
P(y|do(x))=∑zP(y|do(x),z)P(z|do(x))=∑zP(y|do(x),z)P(z)←(Z≺X)Gx=∑zP(y|do(x),x,z)P(z)←(Yx⊥⊥X|Z)Gx=∑zP(y|x,z)P(z)←consistency.
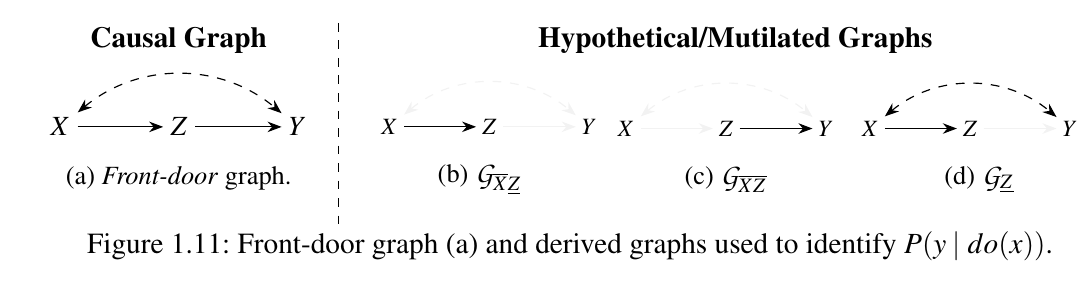
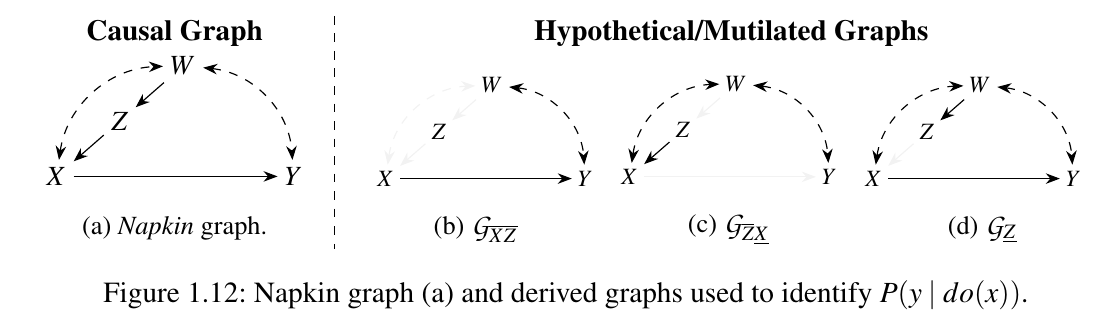
我们再来看这个例子:
Rules:
P(y|do(x))=∑zP(y|do(x),z)P(z|do(x))=∑zP(y|do(x,z))P(z|do(x))←rule2:(Y⊥⊥Z|X)G¯¯¯XZ––=∑zP(y|do(z))P(z|do(x))←rule3:(Y⊥⊥X|Z)G¯¯¯¯¯¯ZX
SWIG:
P(y|do(x))=∑zP(y|do(x),z)P(z|do(x))=∑zP(y|do(x,z),z)P(z|do(x))←consistency=∑zP(y|do(x,z))P(z|do(x))←(Yxz⊥⊥Zx)Gxz=∑zP(y|do(z))P(z|do(x))=∑zP(y|do(z))P(z|x)←(Z⊥⊥X)Gx+consistency=∑zP(z|x)∑x′P(y|do(z),x′)P(x′|do(z))=∑zP(z|x)∑x′P(y|do(z),x′)P(x′)←(X≺Z)=∑zP(z|x)∑x′P(y|z,x′)P(x′)←(Y⊥⊥Z|X)Gz+consistency
注: 想要用 rules 得到相同的结果, 需要额外的 backdoor 推论 (详情回见文章).
最后,
P(y|do(x))=P(y,x|do(z))P(x|do(z))=∑wP(y,x|z,w)P(w)∑wP(x|z,w)P(w).
推导就省略了.


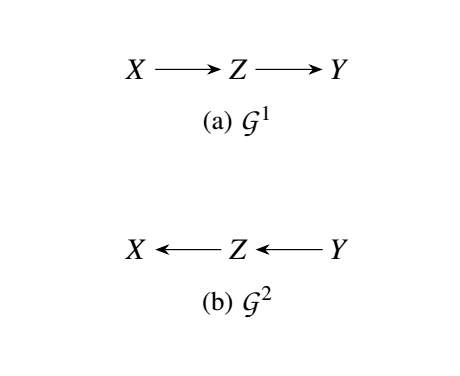




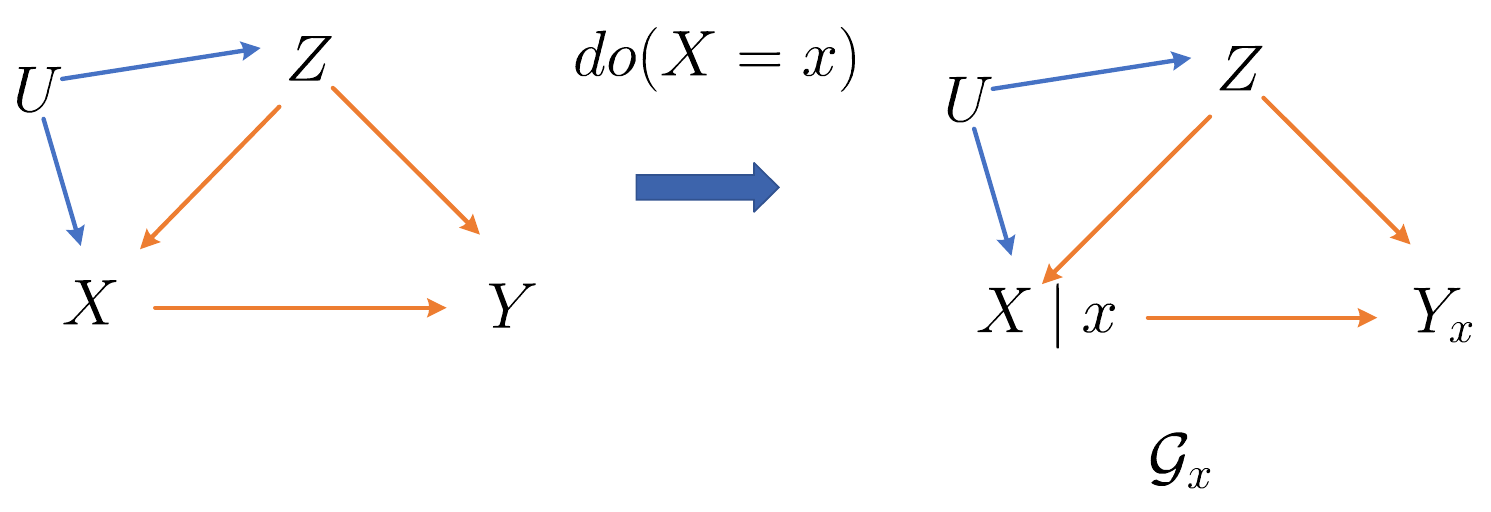







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
2020-07-06 CHARACTERIZING ADVERSARIAL SUBSPACES USING LOCAL INTRINSIC DIMENSIONALITY
2020-07-06 cosface: large margin cosine loss for deep face recognition