Score-Based Generative Modeling through Stochastic Differential Equations

目录

• 概
• 符号说明
  • Wiener process
• 主要内容
  • 反向采样
    • Numerical SDE solvers
    • Predictor-corrector samplers
    • Probability Flow
    • 条件采样
      • 可估计的情况
      • 难以估计的情况
  • 前向扰动
    • SMLD
    • DDPM
    • 拓展
    • sub-VP SDE
  • 具体的采样算法
    • PC sampling
    • Corrector
  • 其它细节
• 代码

Song Y., Sohl-Dickstein J., Kingma D. P., Kumar A., Ermon S. and Poole B. Score-based generative modeling through stochastic differential equations. In International Conference on Learning Representations (ICLR), 2021

概

从 stochastic differential equation (SDE) 角度看 diffusion models.

符号说明

• $\bm{x}(t), t \in [0, T]$ 为 $\bm{x}$ 在时间 $t$ 的一个状态;
• $p_t(\bm{x}) = p(\bm{x}(t))$, $\bm{x}$ 在时间 $t$ 所服从的分布;
• $p_{st}(\bm{x}(t)|\bm{x}(s)), 0 \le s < t \le T$, 从 $\bm{x}(s)$ 到 $\bm{x}(t)$ 的转移核 (transition kernel);
• $\bm{s}_{\theta}(\bm{x}, t)$, 为 score $\nabla_{\bm{x}} \log p_t(\bm{x})$ 的一个近似, 通常用神经网络拟合.

Wiener process

Wiener process $X(t, w)$ 是这样的一个随机过程:

1. $X(0) = 0$;
2. $X(t+\Delta t) - X(t)$ 和 $X(s)$ 是独立的 (感觉就是马氏性);
3. $X(t + \Delta t) - X(t) \sim \mathcal{N}(0, \Delta t)$, 服从方差为 $\Delta t$ 的正态分布;
4. $\lim_{\Delta \rightarrow 0} X(t + \Delta t) = X(t)$, 关于 $t$ 是连续的.

本文所关注的是带 drift $\mu$ 的 Wiener 随机过程:

$$X(t, w) = \mu t + \sigma W_t,$$

其中 $W_t$ 服从一般的 Wiener process.

我们可以用下列的 SDE 来描述该随机过程中的增量 (一般形式):

$$\tag{SDE+} \text{d} \bm{x} = \bm{f}(\bm{x}, t) \text{d} t + \bm{G}(\bm{x}, t) \text{d} \bm{w},$$

其中

$$\bm{f}(\cdot, t): \mathbb{R}^d \rightarrow \mathbb{R}^d, \\ \bm{G}(\cdot, t): \mathbb{R}^d \rightarrow \mathbb{R}^{d \times d}.$$

其中 $\text{d} \bm{w}$ 特指一般 Wiener process 中的增量, 即 $\bm{w}(t + \Delta t) - \bm{w}(t) \sim \mathcal{N}(\bm{0}, \Delta t)$.

它的逆过程可以描述为:

$$\tag{SDE-} \text{d} \bm{x} = \{ \bm{f}(\bm{x}, t) - \nabla \cdot [\text{G}(\bm{x}, t) \bm{G}(\bm{x}, t)^T] - \bm{G}(\bm{x}, t) \bm{G}(\bm{x}, t)^T \nabla_{\bm{x}} \log p_t(\bm{x}) \} \text{d} t + \bm{G}(\bm{x}, t) \text{d} \bm{w}.$$

主要内容

SMLD 和 DDPM 采用了:

1. $\bm{x}(0) \rightarrow \bm{x}(T)$, 逐渐加噪的过程;
2. $\bm{x}(T) \rightarrow \bm{x}(0)$, 逐步采样的过程.

而这两个方程可以看成是两个(正反) SDE 的离散过程.

反向采样

我们首先讲反向采样, 这样会更容易理解前向中的一些设计. 我们知道, 一旦有了 (SDE-) 和 score function $\nabla_x \log p_t(\bm{x})$, 就可以通过一些离散求解方法去逐步'生成'解 $\bm{x}(0)$ 了.

Numerical SDE solvers

有很多数值解法可以用于反向采样: Euler-Maruyama, stochastic Runge-Kutta methods, Ancestral sampling.

本文提出了一种 reverse diffusion sampling (Ancestral sampling 是这个的一特例):

1. 对于
   $$\text{d} \bm{x} = \bm{f}(\bm{x}, t) \text{d} t + \bm{G}(\bm{x}, t) \text{d} \bm{w},$$
   采用
   $$\bm{x}_{i + 1} = \bm{x}_i + \bm{f}_i(\bm{x}_i) + G_i \bm{z}_i, i=0,1,\cdots, N - 1$$
   的更新方式;
2. 类似地, 对于(简化)
   $$\text{d} \bm{x} = \{ \bm{f}(\bm{x}, t) - \bm{G}(\bm{x}, t) \bm{G}(\bm{x}, t)^T \nabla_{\bm{x}} \log p_t(\bm{x}) \} \text{d} t + \bm{G}(t) \text{d} \bm{w},$$
   采用 (注意, 符号是反的)
   $$\bm{x}_i = \bm{x}_{i + 1} - \bm{f}_{i+1}(\bm{x}_{i+1}) + \bm{G}_{i+1} \bm{G}_{i+1}^T \nabla_{\bm{x}} \log p_{i+1}(\bm{x}_{i+1}) + \bm{G}_{i+1} \bm{z}_{i+1}.$$

Predictor-corrector samplers

假设我们知道 $\nabla_x \log p_t(\bm{x})$ 或者它的一个近似 $\bm{s}_{\theta}(\bm{x}, t)$. 我们就可以通过 score-based MCMC 来采样了, 比如 Langevin MCMC 和 HMC (here).

利用 Langevin MCMC, 步骤如下:

$$\bm{x} \leftarrow \bm{x} + \epsilon \nabla_x \log p(\bm{x}) + \sqrt{2\epsilon} \bm{z}, \: \bm{z} \mathop{\sim} \limits^{i.i.d.} \mathcal{N}(\bm{0}, I),$$

其中 $\epsilon$ 为步长.

注: MCMC 采样的过程是保证连续采样的点最终趋向于分布 $p(\bm{x})$, 而不是说整个流程产生点符合 inverse 随机过程 !

整体的 PC samplers 框架如下:

其中 Predictor 可以是任意的 numeric solvers, Corrector 是 MCMC. 这相当于, 通过数值求解随机过程, 但是由于存在误差, 可能导致实际的 $\bm{x}_i$ 偏离它的分布, 故再通过 MCMC 进行纠正.

Probability Flow

这部分, 作者将 SDE 转换成了一个 ODE, 从而能够确定性地采样, 但是这部分内容没怎么看懂, 就只在这里记一笔. 需要注意的是, 和 SDE 不一样, 因为 ODE 不含随即项, 故我们可以通过现成的 black-box ODE solver 来求解方程, 并且通过给定不同的 $\bm{x}(T) \sim p_T$, 便能有不同的解.

其大致流程如下:

$$\bm{x}_i = \bm{x}_{i + 1} - \bm{f}_{i + 1}(\bm{x}_{i + 1}) + \frac{1}{2}G_{i+1}G_{i+1}^T \bm{s}_{\theta}(\bm{x}_{i + 1}, i + 1), \: i=0, 1, \cdots, N - 1.$$

条件采样

条件采样, 即给定 $\bm{y}(0)$, 我们希望从条件分布

$$p(\bm{x}(0) |\bm{y}(0))$$

中采样. 一般来说, 我们会通过贝叶斯公式得到

$$p(\bm{x}(0) |\bm{y}(0)) = \frac{p(\bm{y}(0)|\bm{x}(0)) p(\bm{x}(0))}{p(\bm{y}(0))},$$

但是我们通常难以估计先验 $p(\bm{x}(0))$ 和 $p(\bm{y}(0))$.

我们可以通过下列的 inverse-time SDE 来从 $p_t(\bm{x}(t) | \bm{y})$ 中采样:

$$\text{d} \bm{x} = \{ \bm{f}(\bm{x}, t) - \nabla \cdot [\text{G}(\bm{x}, t) \bm{G}(\bm{x}, t)^T] - \bm{G}(\bm{x}, t) \bm{G}(\bm{x}, t)^T \nabla_{\bm{x}} \log p_t(\bm{x}(t)|\bm{y}(0)) \} \text{d} t + \bm{G}(\bm{x}, t) \text{d} \bm{w}.$$

又

$$\nabla_x \log p_t (\bm{x}(t)|\bm{y}(0)) = \underbrace{\nabla_x \log p_t(\bm{x}(t))}_{\approx s_{\theta}(\bm{x}, t)} + \nabla_{x} \log p_t(\bm{y}(0)|\bm{x}(t)),$$

故当 $\nabla_x \log p_t (\bm{y}(0)|\bm{x}(t))$ 可知时, 我们就可以采样了.

接下来, 我们讨论 $p_t(\bm{y}(0)|\bm{x}(t))$ 可估计和难以直接估计的情况

可估计的情况

1. $\bm{y}(0)$ 为分类任务中的标签;
2. 采样 $\bm{x}(t)$;
3. 利用交叉熵损失 训练一个 time-dependent 分类器:
   $$p_t(\bm{y}(0) | \bm{x}(t)).$$

难以估计的情况

此时我们注意到:

$$\nabla_x \log p_t(\bm{x}(t)|\bm{y}) = \nabla_x \log \int p_t(\bm{x}(t) | \bm{y}(t), \bm{y}(0)) p(\bm{y}(t) | \bm{y}(0)) \text{d} \bm{y}(t).$$

我们给出下面两个合理的假设:

1. $p(\bm{y}(t) | \bm{y}(0))$ 是可求的;
2. $p_t(\bm{x}(t)|\bm{y}(t), \bm{y}(0)) \approx p_t(\bm{x}(t)|\bm{y}(t))$, 这是因为对于 $t$ 比较小的情况, $\bm{y}(t) \approx \bm{y}(0)$, 而对于 $t$ 比较大的情况, $\bm{x}(t)$ 受 $\bm{y}(t)$ 影响最大.

此时有

$$\begin{array}{ll} \nabla_x \log p_t(\bm{x}(t)|\bm{y}(0)) &\approx \nabla_x \log \int p_t(\bm{x}(t) | \bm{y}(t)) p(\bm{y}(t) | \bm{y}(0)) \text{d} \bm{y}(t) \\ &\approx \log p_t(\bm{x}(t)|\hat{\bm{y}}(t)) \: \leftarrow \hat{\bm{y}}(t) \sim p(\bm{y}(t)|\bm{y}(0)) \\ &=\nabla \log_x p_t(\bm{x}(t)) + \nabla_x \log p_t(\hat{\bm{y}}(t)|\bm{x}(t)) \\ &\approx \bm{s}_{\theta} (\bm{x}(t), t) + \nabla_x \log p_t(\hat{\bm{y}}(t) | \bm{x}(t)). \end{array}$$

此时只要 $\nabla_x \log p_t(\hat{y}(t)|\bm{x}(t))$ 可知便可代入求解了.

下面以 Imputation 为例进行讲解. 假设 $\Omega(\bm{x}), \bar{\Omega}(\bm{x})$ 分别表示 观测的 和 缺失的 部分. 我们的目的是从

$$p(\bm{x}(0) | \Omega(\bm{x}(0)) = \bm{y})$$

中采样. 按照上面的步骤, 我们只需要估计

$$\nabla_x \log p_t (\bm{x}(t) | \hat{\Omega}(\bm{x}(t)) )$$

即可. 实际上, 注意到由于本文的建模都是 element-wise 的, 所以

$$p_t (\bm{x}(t) | \hat{\Omega}(\bm{x}(t)) ) = p_t (\bm{x}_{\hat{\Omega}}(t)),$$

即仅 $\hat{\Omega}$ 区域需要采样.

注: 这里的内容和原文 Appendix I.2 的推导有较大出入, 我是按照我自己的理解来的, 也没有实验过, 准确性存疑 !

前向扰动

根据前面的流程, 我们知道, 倘若我们能够估计出

$$\bm{s}_{\theta}(\bm{x}, t) \approx \nabla_x \log p_t (\bm{x}),$$

那么我们就可以跟着随机过程一步一步地采样了, 而这需要用到 (denosing) score matching 作为训练目标:

$$\theta^* = \mathop{\arg \min} \limits_{\theta} \mathbb{E}_t \Bigg\{ \lambda (t) \mathbb{E}_{\bm{x}(0)} \mathbb{E}_{\bm{x}(t)|\bm{x}(0)} [\|\bm{s}_{\theta}(\bm{x}(t), t) - \nabla_{\bm{x}(t)} \log p_{0t} (\bm{x}(t)|\bm{x}(0))\|_2^2] \Bigg\},$$

其中 $\lambda(\cdot)$ 为正的权重, 通常选择 $\lambda \propto 1 / \mathbb{E} [\|\nabla_{\bm{x}(t)} \log p_{0t} (\bm{x}(t)|\bm{x}(0))\|_2^2]$, $t \sim \mathcal{U}[0, T]$.

从上面目标函数的定义可知, 一般来说, 只有 $p_{0t}$ 是显式可求的上面的才有意义, 对于更加一般的随机过程, 可以用 slice score matching 来绕开其中复杂的计算 (不过需要以更多的计算量为代价). 下面所介绍的, 都是可求的高斯分布.

SMLD

SMLD 定义了 $\{\bm{x}_i\}_{i=1}^N$, 可以看成是 $t = \frac{i}{N} \in [0, T = 1]$ 的离散的随机过程:

$$\tag{1} \bm{x}_i = \bm{x}_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2} \bm{z}_{i-1}, \: \bm{z}_i \mathop{\sim} \limits^{i.i.d.} \mathcal{N}(\bm{0}, I).$$

且满足

$$\sigma_{\min} = \sigma_1 < \sigma_2 < \cdots < \sigma_N = \sigma_{\max}.$$

此时有:

$$\bm{x}_i|\bm{x}_0 \sim \mathcal{N}(\bm{x}_0, \sigma_i^2 I).$$

我们进一步将其改写成 SDE 的形式 (即令 $N \rightarrow \infty$ ):

$$\Delta \bm{x}(t) = \bm{x}(t + \Delta) - \bm{x}(t) = \sqrt{\Delta \sigma^2 (t)} \bm{z}(t) = \sqrt{\frac{\Delta \sigma^2(t)}{\Delta t} \Delta t} \bm{z}(t),$$

当 $\Delta t \rightarrow 0$ 时 (即 $N \rightarrow \infty$ ) 有:

$$\Delta \bm{x}(t) \rightarrow \text{d} \bm{x}(t), \\ \frac{\Delta \sigma^2 (t)}{\Delta t} \rightarrow \frac{\text{d}[\sigma^2(t)]}{\text{d}t}.$$

最后, 我们容易发现增量 $\sqrt{\Delta t} \bm{z}(t) \sim \mathcal{N}(\bm{0}, \Delta t)$, 所构成的随机过程自然满足 Wiener process, 故

$$\tag{2} \text{d}\bm{x} = \bm{0} \text{d}t + \sqrt{\frac{\text{d} \sigma^2 (t)}{\text{d} t}} \text{d} \bm{w}.$$

即不存在 drift 量.

DDPM

DDPM 定义了 $\{\bm{x}_i\}_{i=1}^N$, 可以看成是 $t = \frac{i}{N} \in [0, T = 1]$ 的离散的随机过程:

$$\tag{3} \bm{x}_i = \sqrt{1 - \beta_i} \bm{x}_{i-1} + \sqrt{\beta_i} \bm{z}_{i-1}, \bm{z}_i \mathop{\sim} \limits^{i.i.d.} \mathcal{N}(\bm{0}, I).$$

令 $\bar{\beta}_i := N \beta_i$, 并定义

$$\beta(t), t \in [0, 1], \: \beta(\frac{i}{N}) = \bar{\beta_i}.$$

则 (3) 可以改写为

$$\tag{3+} \bm{x}(t + \Delta t) - \bm{x}(t) = (\sqrt{1 - \beta(t + \Delta t) \Delta t} - 1) \bm{x}(t) + \sqrt{\beta (t + \Delta t) \Delta t} \bm{z}(t),$$

当 $\Delta \rightarrow 0$, 有

$$\bm{x}(t + \Delta t) - \bm{x}(t) = \Delta \bm{x}(t) \rightarrow \text{d} \bm{x}(t) \\ \sqrt{1 - \beta(t + \Delta t) \Delta t} - 1 \rightarrow -\frac{1}{2} \beta (t) \text{d} t \\ \sqrt{\beta (t + \Delta t) \Delta t} \bm{z}(t) \rightarrow \sqrt{\beta (t)} \text{d}\bm{w}.$$

其中第二项由一阶泰勒近似可以得到, 第二项和 SMLD 中的推理是类似的.

最后, 可以总结为如下的 Wiener process:

$$\tag{4} \text{d}\bm{x} = -\frac{1}{2} \beta (t) \bm{x} \text{d} t + \sqrt{\beta (t)} \text{d}\bm{w}.$$

接下来我们推导一下 DDPM 的 $\bm{x}(t)$ 的条件分布. (3+) 两边取期望可知

$$\bm{e}(t + \Delta t) - \bm{e}(t) = (\sqrt{1 - \beta(t + \Delta t) \Delta t} - 1) \bm{e}(t) + \bm{0},$$

其中 $\bm{e}(t) = \mathbb{E}[\bm{x}(t)]$, 则

$$\text{d} \bm{e} = -\frac{1}{2} \beta (t) \bm{e} \text{d} t,$$

加上初值条件 $\bm{e}(0) = \bm{e}_0$, 可得:

$$\bm{e}(t) = \bm{e}(0) e^{-\frac{1}{2} \int_0^t \beta (s) \text{d}s}.$$

而 $\bm{x}(t)$ 的协方差矩阵 $\Sigma_{VP}(t)$ 满足

$$\text{d}\Sigma_{VP}(t) = \beta (t) (I - \Sigma_{VP}(t)) \text{d}t,$$

加上初始值 $\Sigma_{VP}(0)$可得

$$\Sigma_{VP}(t) = I + e^{-\int_0^t \beta(s) \text{d}s} (\Sigma_{VP}(0) - I).$$

故服从

$$\bm{x}(t)|\bm{e}(0) \sim \mathcal{N}(\bm{e}(0) e^{-\frac{1}{2} \int_0^t \beta (s) \text{d}s}; I + e^{-\int_0^t \beta(s) \text{d}s}(\Sigma_{VP}(0) - I))$$

在已知 $\bm{x}(0)$ 的条件下, $\bm{e}(0) = \bm{x}(0), \Sigma_{VP}(0) = 0$, 故

$$\bm{x}(t)|\bm{x}(0) \sim \mathcal{N}(\bm{x}(0) e^{-\frac{1}{2} \int_0^t \beta (s) \text{d}s}; I - e^{-\int_0^t \beta(s) \text{d}s}I)$$

注: 方差的公式的推导在另一篇论文中, 这里的方差求解是一般的基础的.

拓展

通过 SMLD 和 DDPM 两个例子可以发现, 我们只需要个性化定制 $\bm{f}(\bm{x}, t)$ 和 $\bm{G}(\bm{x}, t)$, 即可构造不同的前向扰动过程. 实际上, SMLD 和 DDPM 代表了两种不同的 SDE: Variance Exploding (VE) SDE 和 Variance Preserving (VP) SDE. 这是因为 SMLD 要求 $\sigma_{\max} \rightarrow \infty$ 而由上面的推导可得, 倘若 $\Sigma_{VP}(0) = I$ 或者 $\int_{0}^t \beta (s) \text{d}s \rightarrow +\infty$时, 方差都是收敛的.

sub-VP SDE

受 DDPM VP SDE 性质的启发, 作者设计了一种新的前向扰动过程:

$$\text{d}\bm{x} = -\frac{1}{2} \beta(t) \bm{x} \text{d}t + \sqrt{\beta (t) (1 - e^{-2 \int_0^t \beta (s) \text{d} s})} \text{d} \bm{w}.$$

和 DDPM 一样, $\bm{x}(t)$ 的期望

$$\mathbb{E}[\bm{x}(t)] = \mathbb{E}[\bm{x}(0)] e^{-\frac{1}{2} \int_0^t \beta (s) \text{d}s}.$$

而协方差为

$$\Sigma_{sub-VP}(t) := \text{Cov}[\bm{x}(t)] = I + e^{-2\int_0^t \beta(s) \text{d}s} I + e^{-\int_0^t \beta(s) \text{d}s} (\Sigma_{sub-VP}(0) - 2I).$$

它有两个性质:

1. 当 $\Sigma_{VP}(0) = \Sigma_{sub-VP}(0)$时, $\Sigma_{sub-VP} \preceq \Sigma_{VP}$, 即拥有更小的方差;
2. $\lim_{t \rightarrow} \Sigma_{sub-VP}(t) = I$ 当 $\int_0^{+\infty} \beta(s) \text{d} s = +\infty$.

此外它的条件分布为:

$$\bm{x}(t)|\bm{x}(0) \sim \mathcal{N}(\bm{x}(0) e^{-\frac{1}{2} \int_0^t \beta (s) \text{d}s}; (1 - e^{-\int_0^t \beta(s) \text{d}s})^2 I).$$

具体的采样算法

PC sampling

Corrector

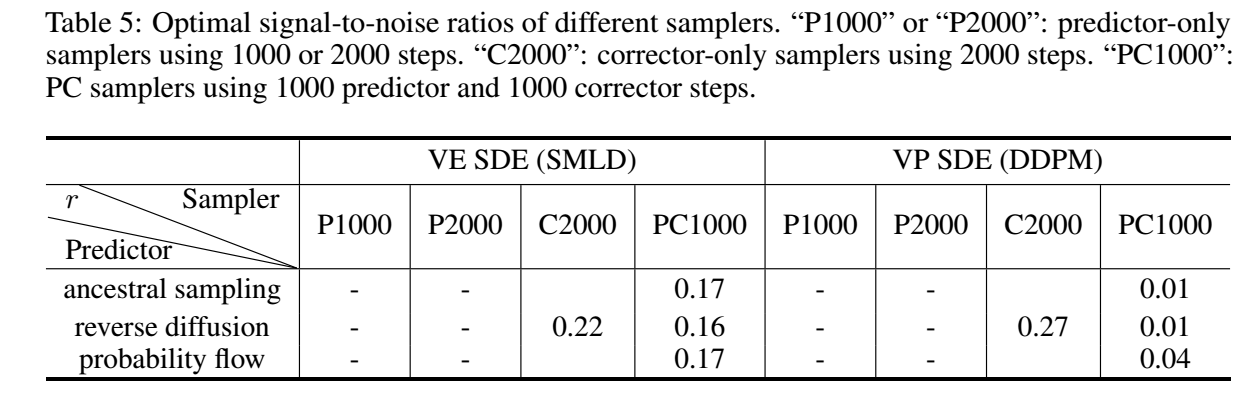
这里, 作者直接构造步长, 需要注意的是, 这里的 $r$ 代表信噪比.

其它细节

• 网络结构: 和 DDPM 中的一致;
• 训练采用 $N=1000$ scales;
• 采样的时候, 最后得到的 $\bm{x}(0)$ 会带有人眼无法察觉但是影响 FID 指标的噪声, 故需要在结束的时候和 DDPM 一样接入去噪环节 (Tweedies' formula);
• 虽然训练的时候采取 $N=1000$, 但是采样的时候可以 $N=2000$ 甚至更多, 这个时候需要插值, 比如

$$\bm{s}_{\theta}' (\bm{x}, i) \rightarrow \bm{s}_{\theta}' (\bm{x}, i / 2), \\ \bm{s}_{\theta}' (\bm{x}, i) \rightarrow \bm{s}_{\theta}' (\bm{x}, \lfloor i / 2 \rfloor);\\ $$

• 最优的 信噪比 (singal-to-noise) $r$ 如下图所示:

代码

[official]