How Powerful is Graph Convolution for Recommendation?

概
符号说明
主要内容
代码

Shen Y., Wu Y., Zhang Y., Shan C., Zhang J., Letaief K. B. and Li D. How powerful is graph convolution for recommendation? In ACM International Conference on Information and Knowledge Management (CIKM), 2021.

概

本文从 low-pass filters 的角度将经典的用于推荐系统的GCN, MF 模型进行了统一, 特别地, 给出了一个显式的求解方法, 无需训练.

这里的介绍结构和原文有些出入, 首先介绍基本的概念, 然后说明 smoothness 的重要性, 再介绍一些现有的 low-pass filters, 最后再给出本文所提出的 GF-CF.

符号说明

$u \in \mathcal{U}$, 用户;
$i \in \mathcal{I}$, item;
$n = |\mathcal{U}| + |\mathcal{I}|$;
$R \in \{0, 1\}^{|\mathcal{U}| \times |\mathcal{I}|}$, 交互矩阵;
$\bm{r}_u \in \{0, 1\}^{|\mathcal{I}|}$, 为 $R$ 的第 $u$ 行;
邻接矩阵,
\[A = \left [ \begin{array}{cc} \bm{0} & R \\ R^T & \bm{0} \end{array} \right ] \in \{0, 1\}^{n \times n}; \]
$\mathcal{N}_k, k = 1,2, \cdots, n$, 为结点 $k$ 所对应的邻居的集合;
$N_k = |\mathcal{N}_k|$;
$D_U := \text{Diag}(R \bm{1}) \in \{0, 1\}^{|\mathcal{U}|\times|\mathcal{U}|}, D_I := \text{Diag}(\bm{1}^T R) \in \{0, 1\}^{|\mathcal{I} \times |\mathcal{I}|}$, 对角线元素分别为 $R$ 的行和和列和;
$D := \text{Diag} (A \bm{1}) \in \mathbb{R}^{n \times n}$;
normalized rating matrix:
\[\tilde{R} = D_U^{-\frac{1}{2}} R D_{I}^{-\frac{1}{2}} \in \mathbb{R}^{|\mathcal{U}| \times |\mathcal{I}|}; \]
$\tilde{\bm{r}}_u \in \mathbb{R}^{|\bm{I}|}$, 为 $\tilde{R}$ 的第 $u$ 行;
$\bar{\bm{r}}_u$ 是 $\tilde{\bm{r}}_u$ 的某种变换后的结果;
normalized 邻接矩阵,
\[\tilde{A} = \left [ \begin{array}{cc} \bm{0} & \tilde{R} \\ \tilde{R}^T & \bm{0} \end{array} \right ] \in \mathbb{R}^{n \times n}; \]
item-item normalized adjacency matrix:
\[\tilde{P} = \tilde{R}^T \tilde{R} \in \mathbb{R}^{|\mathcal{I}| \times |\mathcal{I}|}; \]
$S \in \mathbb{R}^{|\mathcal{U}| \times |\mathcal{I}|}$, 每个用户给每个 item 的打分;
$\bm{s}_u \in \mathbb{R}^{I}$, 用户 $u$ 对各 items 的打分情况.

主要内容

smoothness 的重要性

在开始部分内容之前, 请先了解 [LightGCN].

LightGCN 根据内积 $\bm{e}_u^T \bm{e}_i$ 进行预测, 并通过 BPR 进行训练;
下面定理给出了 1 层 LightGCN 的一个性质:

定理3.1: 令 $N_{\max} = \max_i N_i, N_{\min} = \max_i N_i, \: i \in \mathcal{U} \cup \mathcal{I}$. 如果 $E^{(0)} \in \mathbb{R}^{(|\mathcal{I}| + |\mathcal{U}|) \times d}$ 服从独立同分布的(单位球上)均匀分布(即, $\|\bm{e}^{(0)}\|_2 = 1$)且

\[d > \frac{C N_{\max}^3 \log (|\mathcal{I}| + |\mathcal{U}|)}{N_{\min}}, \]

则对于一层的 LightGCN 有

\[\mathbb{P}(\{{\bm{e}_u^{(1)}}^T \bm{e}_i^{(0)} > \{{\bm{e}_u^{(1)}}^T \bm{e}_j^{(0)}| (u, i) \in \mathcal{S}_1, (u, j) \in S_2 \}) \ge 3 / 4, \]

其中 $C$ 为常数,

\[\mathcal{S}_1 = \{(u, i) | R_{u, i} = 1\}; \\ \mathcal{S}_2 = \{(u, i) | R_{u, i} = 0\}. \]

互相干性 (mutual coherence): 矩阵 $A \in \mathbb{C}^{d \times m}$的各列满足 $a_i^H a_i = 1$, 则矩阵 $A$ 的互相干性定义为:
$$
M_A = \max_{1 \le i \not= j \le m} |a_i^H a_j|.
$$

注: 下面的互相干性是基于行的.

proof:

令

\[\epsilon = M_{E^{(0)}}, \]

则

\[\begin{array}{ll} {\bm{e}_u^{(1)}}^T \bm{e}_i^{(0)} -{\bm{e}_u^{(1)}}^T \bm{e}_j^{(0)} &= \frac{1}{\sqrt{N_u}}(\sum_{k \in \mathcal{N}_u} \frac{1}{\sqrt{N}_k} \bm{e}_k^{(0)})^T (\bm{e}_i^{(0)} - \bm{e}_j^{(0)}) \\ &\ge \frac{1}{\sqrt{N_u}}(\sum_{k \in \mathcal{N}_u} \frac{1}{\sqrt{N}_k} ({\bm{e}_k^{(0)}}^T (\bm{e}_i^{(0)} - \bm{e}_j^{(0)})) \\ &\ge \frac{1}{\sqrt{N_u}}(\sum_{k \in \mathcal{N}_u} \frac{1}{\sqrt{N}_k} ({\bm{e}_k^{(0)}}^T \bm{e}_i^{(0)} - \epsilon)) \quad \leftarrow j \not \in \mathcal{N}_u \\ &\ge \frac{1}{\sqrt{N_u}}(\frac{1}{\sqrt{N_i}} - \frac{N_u - 1}{\sqrt{N_{\min}}} \epsilon - \frac{N_u}{\sqrt{N}_{\min}} \epsilon) \quad \leftarrow i \in \mathcal{N}_u \\ &= \frac{1}{\sqrt{N_u}}(\frac{1}{\sqrt{N_{\max}}} - \frac{2N_{\max}}{\sqrt{N_{\min}}} \epsilon) \end{array}. \]

根据以下的引理:

引理8.1: 令 $A \in \mathbb{R}^{n \times m}$, 每一行独立在单位球面上均匀采样, 则至少有 3/4 的概率使得

\[M_{A} \le C\sqrt{\frac{\log n}{m}} \]

成立, 其中 $C$ 为正常数.

于是,
$$
d > \frac{2C^2 N_{\max}^3 \log (|\mathcal{I}| + |\mathcal{U}|)}{N_{\min}},
$$
时, 有

\[\epsilon < \sqrt{\frac{N_{\min}}{2N_{\max}^3}} \]

成立 (3/4 概率).

此时,

\[{\bm{e}_u^{(1)}}^T \bm{e}_i^{(0)} - {\bm{e}_u^{(1)}}^T \bm{e}_j^{(0)}>\frac{1}{\sqrt{N_u}}(\frac{1}{\sqrt{N_{\max}}} - \frac{1}{\sqrt{2N_{\max}}}) > 0. \]

上面的定理告诉我们:

即使是随机初始化, 凭借聚合效应, 使得整个图平滑后也能产生不错的推荐效果 (训练集);
数据的密度越大, 所需的维度 $d$ 也应当越大;
实际上概率 $3/4$ 可以进一步提升以逼近概率 $1$, 只是条件需要加强.

实际上, 可以通过如下的一个实验发现, 随着 $d$ 的增加, 随机初始化的结果以及和用BPR训练的结果相媲美了.

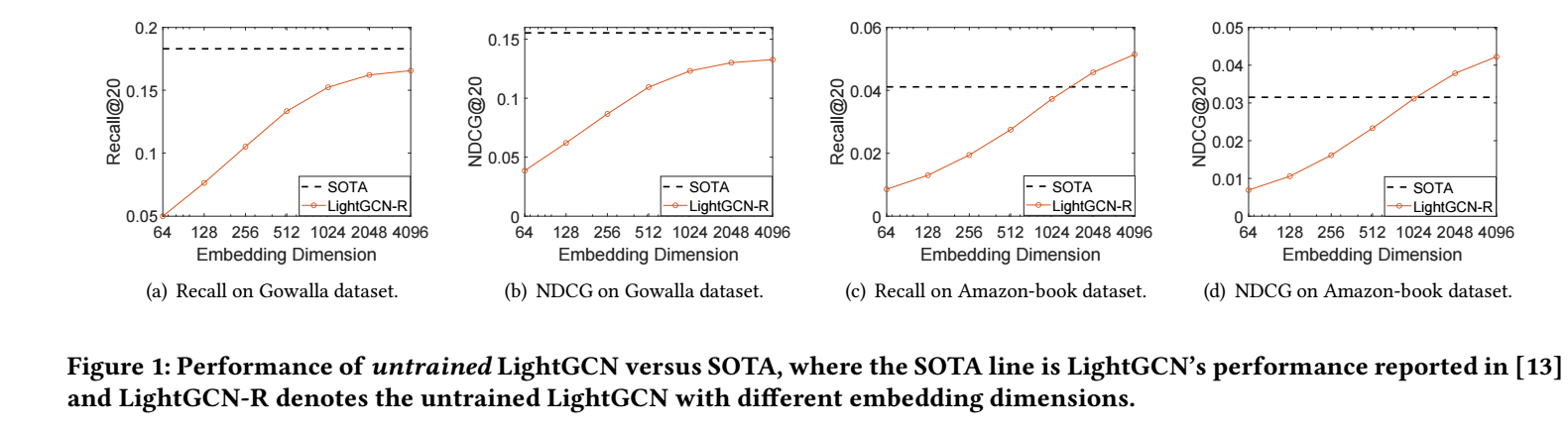
极限的结果 (LGCN-IDE)

从上面的结果可以看出, $d$ 越大, 拟合的结果越好, 那么 $d \rightarrow +\infty$ 的情况是怎么样的呢?

定理3.2: 假设无约束 LightGCN 的 $\bm{E}^{(0)} \in \mathbb{R}^{(|\mathcal{I}| + |\mathcal{U}|) \times d}$ 通过一个零均值, 非零房差的分布进行初始化, 则预测 score 为

\[\bm{s}_u = \sum_{k=0}^{K-1} \beta_k \tilde{\bm{r}}_u (\tilde{R}^T \tilde{R})^k \in \mathbb{R}^{|\mathcal{I}|}, \]

其中 $\beta_k$ 和 LightGCN pooling 各层特征的系数 $\alpha_k$ 有关.

proof:

将 $E^{(k)}$ 拆解为:

\[E^{(k)} = \left [ \begin{array}{c} U^{(k)} \\ V^{(k)} \\ \end{array} \right ] = \left [ \begin{array}{c} \tilde{R} V^{(k - 1)} \\ U^{(k - 1)} \tilde{R}^T \\ \end{array} \right ]. \]

由此可得:

\[\begin{array}{ll} S = UV^T =&(\sum_{i=0}^{2i \le K} \alpha_{2i} (\tilde{R} \tilde{R}^T)^i U^{(0)} +\sum_{i=0}^{2i + 1 \le K} \alpha_{2i + 1} (\tilde{R} \tilde{R}^T)^i \tilde{R} V^{(0)}) \\ &\cdot(\sum_{i=0}^{2i \le K} \alpha_{2i} (\tilde{R}^T \tilde{R})^i V^{(0)} +\sum_{i=0}^{2i + 1 \le K} \alpha_{2i + 1} (\tilde{R}^T \tilde{R})^i \tilde{R}^T U^{(0)})^T. \\ \end{array} \]

假设 $X \in \mathbb{R}^{n \times d}, Y \in \mathbb{R}^{n \times d}$, 每一行都是独立同分布的, 则

\[\lim_{d \rightarrow +\infty} \frac{1}{d} XY^T = \lim_{d \rightarrow +\infty} \frac{1}{d}\sum_{i=1}^d \bm{x}_i \bm{y}_i^T = \mathbb{E}[\bm{x}\bm{y}^T]. \]

其中 $\bm{x}, \bm{y}$ 分别为 $X, Y$ 的列向量.

于是, 观察 $S$ 的展开式可以得到, $U^{0}{V^{(0)}}^T$ 部分由于二者的独立性和零均值性质, 结果都是 $\bm{0}$, 所以只剩下 $U^{(0)}{U^{(0)}}^T$ 和 $V^{(0)}{V^{(0)}}^T$. 经过整理可以得到:

\[\lim_{d \rightarrow \infty} S = \mathbb{E}_{U^{(0)}, V^{(0)}} [S] = \sum_{k=0}^{K-1} \beta_k \tilde{R} (\tilde{R}^T \tilde{R})^k. \]

Graph signal processing

定义图 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$;
令其邻接矩阵为 $A \in \mathbb{R}^{n \times n}$;
graph signal 是一个函数, 定义为:

\[x: \mathcal{V} \rightarrow \mathbb{R}, \]
将结点映射为数, 对于总共用 $n$ 个结点的图来说, 就构成了一 $n$-维的向量 $\bm{x} = [x(i)]_{i \in \mathcal{V}}$;
两个结点阶的梯度由下列公式定义:

\[(\nabla x)_{i, j} = \sqrt{A_{i,j}} (x_i - x_j); \]
定义 graph signal 的光滑性为:

\[\mathcal{S}(\bm{x}) = \frac{1}{2} \|\nabla x\|_F^2 = \frac{1}{2} \sum_{i, j} A_{i, j} (x_i - x_j)^2 = \bm{x}^T L \bm{x}, \]
其中 $L := D - A$ 为 Laplacian 矩阵. 通常, $\frac{S(\bm{x})}{\|\bm{x}\|_2}$ 越小说明整个 graph signal 越光滑;
当 $L$ 是实对称矩阵的时候, 它可以特征分解为

\[L = U\Lambda U^T, \]
其中 $\Lambda = \text{Diag}(\lambda_1, \lambda_2, \cdots, \lambda_n), 0 \le \lambda_1 \le \lambda_2 \le \cdots \le \lambda_n$, $U = [\bm{u}_1, \cdots, \bm{u}_n] \in \mathbb{R}^{n \times n}$ 为所对应的特征向量组;
根据特征分解的性质, 很容易发现:

\[\frac{\mathcal{S}(\bm{x})}{\|\bm{x}\|_2} \ge\frac{\mathcal{S}(\bm{u})}{\|\bm{u}\|_2}, \]
这说明, 对应的特征值越小的 $\bm{u}$, 其光滑性越好, 也就意味着更多的低频信号;
因为高频信号往往代表着噪声, 所以我们希望有一种特征变换 (low-pass filters) 以更好地保留低频信号.
在图卷积中, 通常模仿傅里叶变换, 构造如下形式的变换:

\[\mathcal{H}(L) := U\text{Diag}(h(\lambda_1), \cdots, h(\lambda_n)) U^T; \]
倘若我们把不同的 $\lambda_1$ 看成是不同的频率, 那么 $h(\cdot)$ 就是反映了我们对不同频率的好恶; 于是, 所有的问题就是如何构造 $\mathcal{H}(L)$ 以满足 low-pass filters.

item-item

我们考虑如下的问题:

item-item (normalized) 邻接矩阵 $\tilde{P} = \tilde{R}^T \tilde{R} \in \mathbb{R}^{|\mathcal{I}| \times |\mathcal{I}|}$;
定义 items 的一个 Laplacian 矩阵 $\tilde{L} = I - \tilde{P}$;
将 $\bar{\bm{r}}_u \in \mathbb{R}^{|\mathcal{I}|}$ ($\tilde{\bm{r}}_u$ 的一个变换) 作为 items 的一个图信号;
进行如下的变换:
\[\tag{13} \bm{\bar{s}}_u = \bar{\bm{r}}_u U\text{Diag}(h(\lambda_1), \cdots, h(\lambda_{|\mathcal{I}|})) U^T; \]

注: 把 $\bar{\bm{r}}_u$ 看成是某个用户给予 items 的一个信号, 整个流程会好理解点.

几种不同的 low-pass filters

Linear Filter
\[h(\lambda_i) = \sum_{k=0}^K \alpha_k \lambda_i^k; \]
Ideal Low-pass Filter:
\[h(\lambda_i)= \left \{ \begin{array}{ll} 1, & \text{if } \lambda_i \le \bar{\lambda}; \\ 0, & \text{otherwise}. \end{array} \right . \]
完全阻隔了高频信息;
Opinion Dynamics:
\[h(\lambda_i) = \frac{1}{1 + \tilde{\alpha} \lambda_i}. \]

与现有的方法的联系

low-rank matrix factorization

该方法旨在求解

\[U^*, V^* = \mathop{\text{argmin}} \limits_{U \in \mathbb{R}^{|\mathcal{U}| \times d, V \in \mathbb{R}^{|\mathcal{I}| \times d}}} \|\tilde{R} - UV^T\|_F^2, \: \text{s.t.} V^TV = I. \]

注意到, 最优解是 $U, V$ 分别 $\tilde{R}$ 前 $d$ 个最大的奇异值所对应的左右特征向量, 而 $\tilde{R}$ 最大的恰恰就对于 $\tilde{L}$ 最小的那些特征向量 $V$, 然后

\[U^* = \tilde{R} V. \]

注: 感觉不用像论文中加 $D_I^{\frac{1}{2}}$.
注: 这里的 $V$ 才是 (13) 中的 $U$.

于是:

\[\bm{\bar{s}}_u = V\text{Diag}(h(\lambda_1), \cdots, h(\lambda_{|\mathcal{I}|})) V^T, \]

这里

\[h(\lambda_i) = \bm{1}_{i \le d}, \]

即只保留最小的特征值所对应的特征向量.

这种处理处理方式, 实际上相当于采用 $K \rightarrow \infty$ 层的 spatial convolution, 这会导致输出的结果 over-smoothing (这部分内容请回看原文), 所以并不是特别高效.

linear auto-encoders

这类的预测方式可以归结为

\[\tag{auto} \bar{\bm{s}}_u = \bar{\bm{r}}_u B, \]

其中 $B \in \mathbb{R}^{|\mathcal{I}| \times |\mathcal{I}|}$ 是可学习的参数.

训练目标是

\[\min_B \sum_u \|\bar{\bm{r}}_u - \bar{\bm{r}}_u B \|_2^2. \]

作者考虑如下的情况 ($\bar{\bm{r}} = \tilde{\bm{r}}$):

\[\min_B \|\tilde{\bm{R}} - \tilde{\bm{R}} B \|_F^2 + \mu \|B\|_F^2, \]

此岭回归的结果为

\[B^* = (\tilde{P} + \mu I)^{-1} \tilde{P}. \]

由于对称性, 容易证明 $\tilde{L} = I - \tilde{P}$ 的特征向量和 $B^*$ 的特征向量是一致的, 故 (auto) 也可以转换成 (13) 的形式, 只是:

\[h(\lambda_i) = \frac{1 - \lambda_i}{1 + \mu - \lambda_i}. \]

当 $\mu > 1$, 这等价于一种 $K \rightarrow \infty$, 同时对于系数为 $-(-\frac{1}{\mu})^k$ 的 spatial convolution, 因为层数越深, 影响越小, 故 over-smoothing 的现象得以缓解.

neighborhood-based

这种方式采取

\[\bar{\bm{s}}_u = \bm{r}_u \tilde{P}, \]

所对应的 'low'-pass filters 为

\[h(\lambda_i) = 1 - \lambda_i. \]

因为 $0 \le \lambda_i \le 1$, 故实际上这个操作就是大小倒置.

LGCN-IDE

上面提及的 $d \rightarrow \infty$ 的情形, 实际上等价于

\[h(\lambda_i) = \sum_{k=0}^{K-1} \beta_k (1 - \lambda_i)^k. \]

这个含义就是比 neighborhood-based 的更加复杂一点.

GF-CF

通过前面的分析, 我们大概知道了如何构建 $\mathcal{H}$, 作者通过结合 linear 和 ideal low-pass filters 给出了避免 over-smoothing 的方案:

\[\bm{s}_u = \bm{r}_u (\underbrace{\tilde{R}^T \tilde{R}}_{\text{linear}} + \alpha D_I^{-\frac{1}{2}} \underbrace{\bar{U} \bar{U}^T}_{\text{ideal low-pass}} D_I^{-\frac{1}{2}}) \]

这里 $\bar{U}$ 是 $\tilde{R}$ 的 top-$d$ 奇异向量.

注: 感觉 linear 部分应该是 neighborhood-based 吧.
注: $\alpha$ 是超参数.

代码

[official]

posted @ 2022-06-18 17:07 馒头and花卷阅读(254) 评论(0) 编辑收藏举报

刷新页面返回顶部

馒头and花卷