LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation
概
LightGCN 极大简化了先前的 NGCF (主要去掉了特征转换部分和非线性激活函数部分).
符号说明
- \(u \in \mathcal{U}, |\mathcal{U}| = M\), 用户;
- \(i \in \mathcal{I}, |\mathcal{I}| = N\), item;
- \(R \in \{0, 1\}^{M \times N}\), 交互矩阵, 用户 \(i\) 和 item \(i\) 有交互才为 1 否则为 0;
- \(\mathcal{N}_u = \{i \in \mathcal{I}| R_{ui} = 1\}\);
- \(\mathcal{N}_i = \{u \in \mathcal{U}| R_{ui} = 1\}\);
- \(\bm{e}^{(0)} \in \mathbb{R}^d\), 根据user (item) 的 ID 转换得到的 embedding;
- \(\bm{e}^{(l)} \in \mathbb{R}^d\), GCN 的第 \(l\) 层的一个特征;
- \(E^{(l)} \in \mathbb{R}^{(M + N) \times d}\), 每一行是一个 \(\bm{e}\).
- \(\sigma(\cdot)\), 非线性激活函数.
主要内容
NGCF
- 获取初始的 ID embeddings:\[\bm{e}_u^{(0)}, \bm{e}_i^{(0)}; \]
- NGCG 的每一层通过邻接的结点的特征进行聚合:\[\bm{e}_{u}^{(k+1)} = \sigma(W_1 \bm{e}_u^{(k)} + \sum_{i \in \mathcal{N}_u} \frac{1}{\sqrt{|\mathcal{N_u}| |\mathcal{N}_i| }} (W_1 \bm{e}_i^{(k)} + W_2 (\bm{e}_i^{(k)} \odot \bm{e}_{u}^{(k)}))), \\ \bm{e}_{i}^{(k+1)} = \sigma(W_1 \bm{e}_i^{(k)} + \sum_{u \in \mathcal{N}_i} \frac{1}{\sqrt{|\mathcal{N_u}| |\mathcal{N}_i| }} (W_1 \bm{e}_u^{(k)} + W_2 (\bm{e}_u^{(k)} \odot \bm{e}_{i}^{(k)}))). \]
- 由此得到\[(\bm{e}_u^{(0)}, \cdots, \bm{e}_u^{(L)}), \\ (\bm{e}_i^{(0)}, \cdots, \bm{e}_i^{(L)}); \]
- 连接得到最后的特征:\[\bm{e}_u = \bm{e}_u^{(0)} \oplus \cdots \oplus \bm{e}_u^{(L)}, \\ \bm{e}_i = \bm{e}_i^{(0)} \oplus \cdots \oplus \bm{e}_i^{(L)}; \]
- 通过内积\[\bm{e}_u^T \bm{e}_i \]进行预测.
作者通过消融发现, 特征转换部分 \(W_1, W_2\) 和非线性激活函数是不必要的:
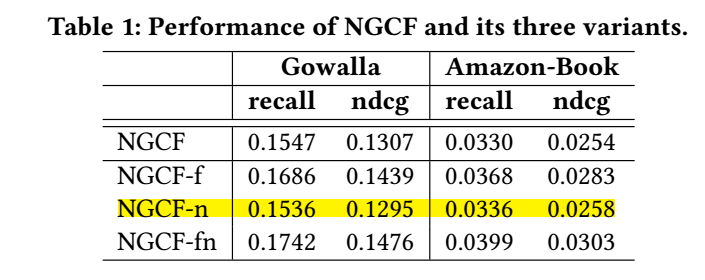
图中:
- NGCF-f: 去掉 \(W_1, W_2\);
- NGCF-n: 去掉 \(\sigma(\cdot)\);
- NGCG-fn: 去掉二者.
LightGCN
为此, 作者提出了一个简化的但更加高效的版本.
-
获取初始的 ID embeddings:
\[\bm{e}_u^{(0)}, \bm{e}_i^{(0)}; \] -
NGCG 的每一层通过邻接的结点的特征进行聚合:
\[\bm{e}_{u}^{(k+1)} = \sum_{i \in \mathcal{N}_u} \frac{1}{\sqrt{|\mathcal{N_u}| |\mathcal{N}_i| }} \bm{e}_i^{(k)}, \\ \bm{e}_{i}^{(k+1)} = \sum_{u \in \mathcal{N}_i} \frac{1}{\sqrt{|\mathcal{N_i}| |\mathcal{N}_u| }} \bm{e}_u^{(k)}; \\ \] -
由此得到
\[(\bm{e}_u^{(0)}, \cdots, \bm{e}_u^{(L)}), \\ (\bm{e}_i^{(0)}, \cdots, \bm{e}_i^{(L)}); \] -
加权和得到最后的特征:
\[\bm{e}_u = \sum_{k=0}^L \alpha_k \bm{e}_u^{(k)}, \\ \bm{e}_i = \sum_{k=0}^L \alpha_k \bm{e}_i^{(k)}, \]这里 \(\alpha_k\) 可以通过诸如注意力网络来学习, 作者推荐直接用 \(\frac{1}{L + 1}\);
-
通过内积
\[\hat{y}_{ui} = \bm{e}_u^T \bm{e}_i \]进行预测;
-
通过 BPR 进行训练:
\[L_{BPR} = - \sum_{u=1}^M \sum_{i \in \mathcal{N}(u)} \sum_{j \not = \mathcal{N}_u} \ln \sigma(\hat{y}_{ui} - \hat{y}_{uj}) + \lambda \|E^{(0)}\|^2. \]
分析
记邻接矩阵
则 LightGCN 的流程可以简述为:
其中 \(D\) 为 \((M + N ) \times (M + N)\) 的对角矩阵, 对角线元素为 \(A\) 每一行的非零元素个数.
记 \(\tilde{A} := D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\), 则最后的加权和的结果可以写为:
有了这些工具可以和以往的一些 GCN 框架进行对比 (不过我一时半会儿也不会回看这些论文, 就不写了). 总体来说, GCN 在推荐系统上的应用效果和 smooth 的程度有很大关系.
实验
- 处理各层 embeddings 的实验:
作者比较了 LightGCN 和 Light-single (仅用最后的 \(\bm{e} := \bm{e}^{L}\) 进行预测), 可以发现, 对于后者, 加深层数是没有丝毫作用的, 大概也是 over-smoothing 了.
- 不同的'标准化'特征方式的影响:
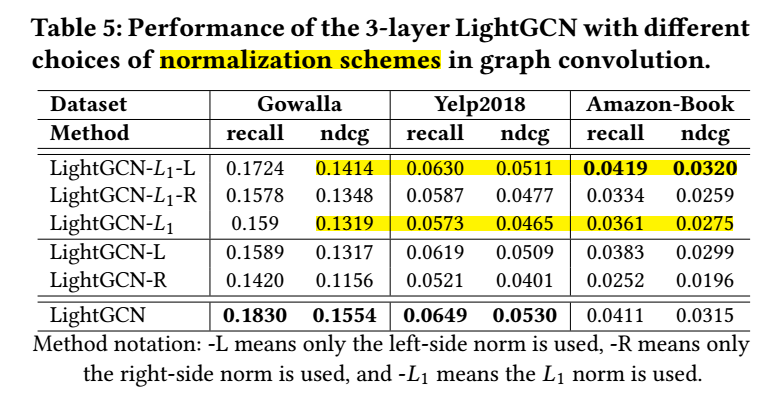
需要注意的是, 无论是 NGCF 还是 LightGCN 都采用了对称的方式'标准化'以避免scale的持续增加, 即 \(\frac{1}{\sqrt{|\mathcal{N}_u ||\mathcal{N}_i|}}\), 作者还比较了仅用一部分的结果. 可以发现, 对于正常的 LightGCN 结果是有提升的, 而在用了 \(L_1\) 之后反而起的反效果 (话说 \(L_1\) 怎么加? \(\frac{\bm{e}}{\|\bm{e}\|_1}\) ?).
- 平滑度量: 作者做了 LightGCN 和 MF 所提取特征的平滑性的比较, 给出了一个指标, 具体回看论文.
代码
[PyTorch]
[TensorFlow]
