Fairness among New Items in Cold Start Recommender Systems
概
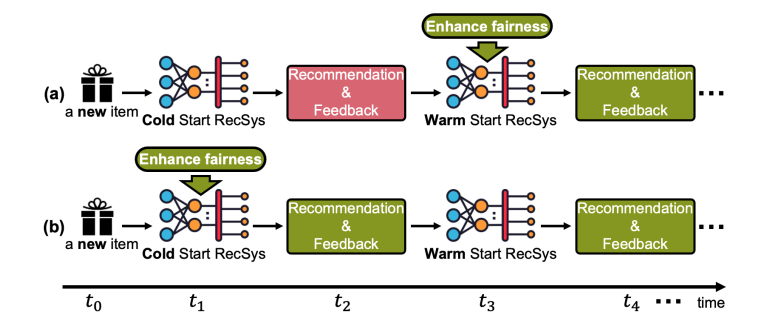
现有的针对 fairness 的文章都是针对 warm start 部分, 大都忽略了在 cold start 阶段的一个 fairness. 本文首先提出一些严格化的度量平衡性的指标, 并提出相应的解决方法.
符号说明
- \(\mathcal{U} = \{1, 2, \cdots, N\}\), 用户;
- \(\mathcal{I}_w = \{1, 2, \cdots, M_w\}\), warm start items, 指那些存在历史交易记录的 items;
- \(\mathcal{O}_{tr} = \{(u, i)\}\), 训练集;
- \(\mathcal{I}_c = \{1, 2, \cdots, M_c\}\), 指那些不存在于训练集中的, 即没有历史交易记录的需要 cold start 的 items;
- \(\mathcal{O}_{te} = \{(u, i)\}\), 测试集;
- \(\mathcal{U}_i^+\), 囊括了和 item \(i\) 有过交互的用户;
Opportunity fairness
opportunity fairness 不同于 demographic parity fairness (它要求, 比如, 所有的 items 有相同的曝光率), 它的要求更加细致, 希望每个 item (或者认为构造的一个 group) 的 TPR 是一致的就行. 我们知道,
这就意味着, 每个 item \(i\) 在其所对应的 \(\mathcal{U}_i^+\) 中的推荐正确率是一致的. 显然这种公平性是兼顾到效率和正确率的公平性, 而非 demographic parity fairness 的过于泛滥的公平性.
Max-Min opportunity fairness
定义: 假设 \(\mathcal{H}\) 是一组推荐系统模型的集合, \(\text{TPR}(i; h)\) 是模型 \(h \in \mathcal{H}\) 关于 item \(i\) 在其 \(\mathcal{U}_i^+\) 上的一个 true positive rate, 则 \(h^*\) 满足 Max-Min Opportunity Fairness, 如果
这意味着, Max-Min Opportunity Fairnes 的目标是优化最坏的(最受歧视的)那批 items 的利益. 通常, 为了度量一个推荐系统 \(h\) 的 Max-Min Opportunity Fairness, 通常用最受歧视的 \(t\%\) items 的 \(\text{TPR}\) 的平均作为一个度量指标.
Mean Discounted Gain (MDG)
一般的 \(\text{TPR}\) 没有兼顾排序的因素, 作者这里提出了另外一种度量 true positive rate 的方式:
其中 \(\hat{z}_{u, i}, i \in \mathcal{I}_c\) 是对 item \(i\) 的一个推荐排序, \(\delta(\cdot)\) 返回 \(1\) 若其中的元素为 true 否则返回 \(0\).
可以发现, \(\text{MGD}_i = 0\), 若推荐系统没有向任何用户推荐 item \(i\). 此外, 若推荐 \(i\) 的序过大, 那么整个值也会偏小.
注: \(\log_2\) 的底是我自己加的, 因为作者设计的这个指标本文就是参考 NDCG, 所以大概就是 \(\log_2\). 这样也能保证 \(\text{MDG}_i \in [0, 1]\).
为了衡量整体性的一个 fairness, 通常我们会使用最受歧视的 \(t\%\) items 的平均作为一个参考指标, 记为 \(\text{MDG-min } t\%\), 为了便于比较, 通常也会给出 \(\text{MDG-max } t\%\). 此外, 我们也可以用
衡量全局的一个性质. 但是需要注意的是, 和 NDCG 不同, \(\text{MDG-all}\) 的最大值往往不是 \(1\).
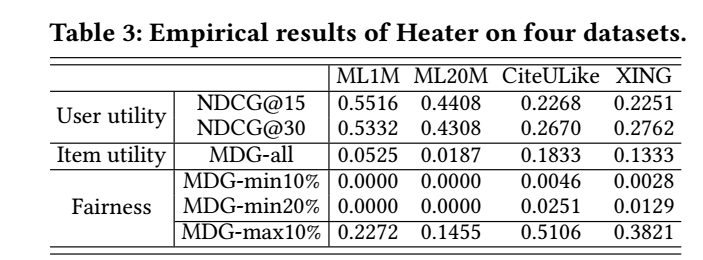
注: 个人感觉, 其实仅凭 \(\text{MDG-all}\) 是看不出 fairness 怎么样的, 需要通过 \(\text{MDG-min}\) 和 \(\text{MDG-max}\) 的一个比较来看是最直接的.
主要内容
针对 fairness 设计模型和框架确实效果会比较好, 但是往往缺乏通用性, 而后处理方法简单且不需要对原有模型进行改变, 但是往往会损害推荐系统的一个性能. 本文提出一种可学习的后处理算法.
基本框架
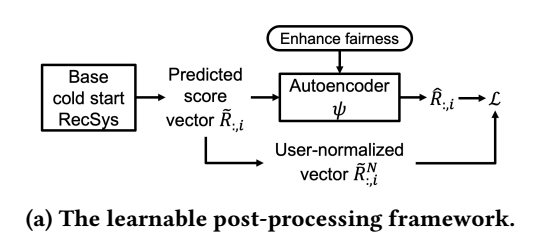
- 基本的推荐系统(固定不变)对 cold start 的 items 给出 score \(\tilde{R}_{:, i} \in \mathbb{R}^N\) (\(N\) 是用户数量);
- 自编码器将 \(\tilde{R}_{:, i}\) 映射为 \(\hat{R}_{:, i} \in \mathbb{R}^{N}\) 用于最后的排序;
- 通过在训练的时候对自编码器注入 fairness 以满足所需性质 (在训练的时候, 只有 warm start items \(\mathcal{I}_w\) 是已知的):
- 对每一个用户在 \(\mathcal{I}_w\) 上的分布进行标准化:\[\tilde{R}_{u, :}^N = (\tilde{R}_{u, :} - \text{Mean}(\tilde{R}_{u, :})) / \text{Std}(\tilde{R}_{u, :}), \]并令 \(\hat{R}_{:, i}\) 靠近 user-normalized 后的 \(\tilde{R}_{:, i}^N\), 这样 re-ranking 后的 score 就都在一个量纲了;
- 此外, 我们希望最受歧视的 item 的 \(\hat{R}_{\mathcal{U}_i^+, i}\) 和最受追捧的 item 的分布是一致的, 这个可以通过以下的两种方式实现.
- 对每一个用户在 \(\mathcal{I}_w\) 上的分布进行标准化:
Joint-learning generative method
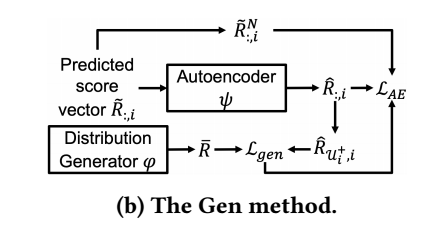
- 生成器 \(\varphi\) 输出分布 \(\bar{P}\);
- 然后每个 item 的各自在 users 上的分布 \(P(\hat{R}_{\mathcal{U}^+_i, i})\) 靠近 \(\bar{P}\), 这样无论是受歧视的还是受追捧的 items 在存在交互上的用户上的分布是一致的;
- 之后, 令生成器输出的分布 \(\bar{P}\) 靠近, items \(P(\hat{R}_{\mathcal{U}_i^+, i})\) 的平均.
具体的, 在实际情况中是如此操作的:
- 生成器 \(\varphi\) 是一个 \(\text{MLP}\), 输入和输出都是 1 维 (输入从标准正态分布中采样), 然后从此分布中采样 \(S\) 个元素得到 \(\bar{R} \in \mathbb{R}^S\);
- 我们希望 \(\bar{R}\) 所隐含的分布与 \(\hat{R}_{\mathcal{U}_i^+, i}\) 所隐含的分布尽可能一致, 作者是通过 MMD 实现的:
具体的形式请参考论文;
- 此外, 根据如下方式来训练 \(\psi\):
这里 \(\mathcal{I}_{UE}\) 表示受歧视的items的集合, 即我们只需要受歧视的items 靠近平均的 \(\bar{R}\).
Score scaling method
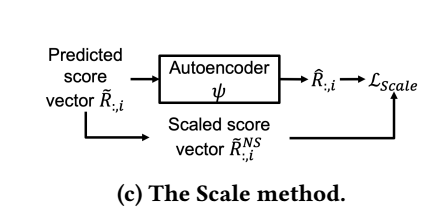
score scaling method 就是对那些受歧视的 items 的分数进行放大:
然后通过如下损失训练 \(\psi\):


